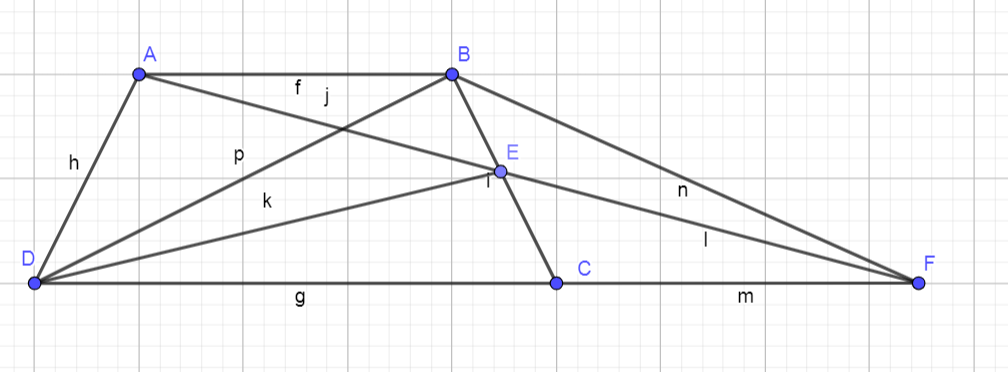
Để giải bài toán, chúng ta sẽ phân tích các thông tin đã cho và sử dụng một số công thức hình học cơ bản để tính diện tích tam giác \( \triangle BFD \).

### Bước 1: Tính độ dài các đáy
Gọi:
- \(AB = a\)
- \(CD = b\)

Theo đề bài, \(AB = \frac{2}{3}CD\):
\[
a = \frac{2}{3}b
\]

### Bước 2: Tính chiều cao hình thang
Diện tích hình thang \(ABCD\) bằng 40 cm². Công thức tính diện tích hình thang là:
\[
S_{ABCD} = \frac{1}{2} (a + b) h
\]

Biết \(S_{ABCD} = 40\), thay \(a = \frac{2}{3}b\) vào ta có:
\[
40 = \frac{1}{2} \left(\frac{2}{3}b + b\right) h
\]
\[
40 = \frac{1}{2} \left(\frac{5}{3}b\right) h
\]
\[
40 = \frac{5}{6}bh
\]
\[
bh = \frac{40 \times 6}{5} = 48
\]
Vậy \(bh = 48\).

### Bước 3: Tính diện tích tam giác \( \triangle AED \)
Diện tích tam giác \( \triangle AED \) đã cho là 22,4 cm².

### Bước 4: Phân tích mối quan hệ giữa các diện tích và đoạn thẳng
Do \(F\) là giao điểm của đường kéo dài \(AE\) và \(DC\), tam giác \( \triangle AED \) chia hình thang thành hai phần với diện tích đã biết.

### Bước 5: Sử dụng tỷ số diện tích để tính diện tích tam giác \( \triangle BFD \)
Diện tích tam giác \( \triangle AED \) và tam giác \( \triangle BFD \) có chung đáy \(AD\), do đó:
\[
\frac{S_{\triangle AED}}{S_{ABCD}} = \frac{22,4}{40} = 0,56
\]

Vì \( \triangle BFD \) và \( \triangle AED \) cùng nằm trong hình thang và có chung đáy \(AD\), ta có:
\[
S_{\triangle BFD} = (1 - 0,56) \times S_{ABCD} = 0,44 \times 40 = 17,6 \text{ cm}^2
\]

Vậy, diện tích tam giác \( \triangle BFD \) là \(17,6 \text{ cm}^2\).

1. Phân tích "địa hình":

Vẽ hình thang ABCD với AB // CD, AB = 2/3 CD
Lấy E trên BC sao cho S(AED) = 22.4 cm²
Kéo dài AE cắt DC tại F

2. "Lên kế hoạch" chinh phục:

Để tìm S(BFD), ta cần "lượn lờ" qua một vài "điểm đến" trước:

Tìm S(ABE): S(ABE) = S(ABCD) - S(AED) - S(CDE)
Tìm tỉ số S(CDE) / S(ABE): Hai tam giác này chung đường cao AH (từ A xuống DC), tỉ số diện tích bằng tỉ số đáy.
Tìm S(BFD): S(BFD) = S(BFE) - S(DFE). Hai tam giác này cũng chung đường cao (từ B xuống DF), tỉ số diện tích bằng tỉ số đáy.

3. "Xuất quân" giải toán:

S(ABE) = 40 - 22.4 - S(CDE) = 17.6 - S(CDE)
S(CDE) / S(ABE) = CD / AB = (3/2)AB / AB = 3/2
=> S(CDE) = (3/2) * S(ABE) = (3/2) * (17.6 - S(CDE))
"Giải" phương trình => S(CDE) = 10.56 cm² , S(ABE) = 7.04 cm²
S(BFD) / S(DFE) = BF / DF = (BC + CF) / DF = (BC/DF) + 1
Do AE/EF = S(ABE)/S(FE) = S(ADE)/S(DFE) = (S(ABE)+S(BCE))/(S(DFE)+S(DCF))
=> AE/EF = (AB/DC) = 2/3
=> BF/DF = (BC + CF) / DF = (BC/DF) + 1 = (AE+EF)/EF = 5/2
=> S(BFD) = (5/2) * S(DFE) = (5/2) * [S(CDE) + S(AED)] = (5/2) * (10.56 + 22.4) = 84 cm²

Kết luận:

Diện tích tam giác BFD là 84 cm².