Bài 26. Cho ∆ABC vuông tại A. Kẻ đường cao AH. Đường phân giác của ABC cắt
AC tại D và cắt AH tại E.
a) Biết AB = 9cm, BC = 15cm. Tính AC?
b) Chứng minh: ΔABC ΔHBA
c) Gọi I là trung điểm của ED. Chứng minh EI /EH
=EA /EB
Quảng cáo
1 câu trả lời 559
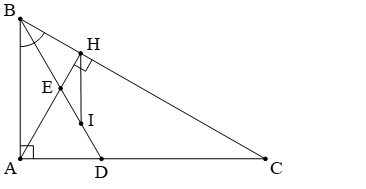
a,
Xét ΔABC vuông tại A có:
BC2= AB2 + AC2 (Đlí Pythagore)
⇔ 152 = 92 + AC2
⇔ AC2 = 225 - 81
⇔ AC2 = 144
⇒ AC = √144 = 12(cm).
b,
Xét ΔABC và ΔHBA có:
⇒ ΔABC ~ ΔHBA(g-g)
c,
\(\widehat{HAE} = \widehat{CAD}\) (do AD là đường phân giác của góc ABC)
\(\widehat{HAE} = \widehat{HDE}\) (do AE // CD)
\(\Rightarrow \Delta AHE \sim \Delta EHD\) (g.g)
=>\(\dfrac{EI}{EA} = \dfrac{EH}{ED}\)
hay \(\dfrac{EI}{EH} = \dfrac{EA}{ED}\)
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
11983
-
5984


