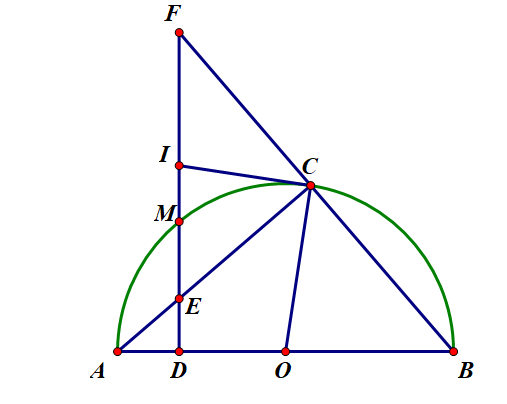
cho nửa đường tròn tâm O đường kính AB. M là điểm bất kì trên cung AB, vẽ MD vuông góc vs AB, trên cung MB lấy C, tiếp tuyến tại C của nửa đường tròn cắt DM tại I;DM cắt AC tại E và cắt BC kéo dài tại F
1)CM: tứ giác BCED: ADCF nội tiếp
2) CM : góc AFE=góc DBE
3) CM: I là tâm đường tròn ngoại tiếp △FEC
Quảng cáo
2 câu trả lời 250
1)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC⊥CB tại C
=>AC⊥BF tại C
Xét tứ giác EDBC có
=>EDBC là tứ giác nội tiếp
Xét tứ giác ADCF có
=>ADCF là tứ giác nội tiếp
3)
EDBC là tứ giác nội tiếp
=>IF=IC
mà IC=IE
nên IF=IC=IE
=>I là tâm đường tròn ngoại tiếp ΔCFE
1)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC⊥CB tại C
=>AC⊥BF tại C
Xét tứ giác EDBC có
ˆEDB+ˆECB=90°+90°=180°EDB^+ECB^=90°+90°=180°
=>EDBC là tứ giác nội tiếp
Xét tứ giác ADCF có
ˆADF=ˆACF=90°ADF^=ACF^=90°
=>ADCF là tứ giác nội tiếp
3)
EDBC là tứ giác nội tiếp
⇒ˆDEC+ˆDBC=180°mà ˆDEC+ˆIEC=180° (kề bù)nên ˆIEC=ˆDBC⇒DEC^+DBC^=180°mà DEC^+IEC^=180° (kề bù)nên IEC^=DBC^
ˆIEC=ˆDBC=12.sđ AC (góc ˆDBC là góc nội tiếp chắn cung AC) ˆICE=sđ CA (góc ˆICE là góc tạo bởi tiếp tuyến IC và dây cung CA)Do đó: ˆIEC=ˆICE⇒IE=ICˆIEC+ˆIFC=90° (ΔFCE vuông tại C)ˆICE+ˆICF=ˆFCE=90°mà ˆIEC=ˆICEnên ˆIFC=ˆICF IEC^=DBC^=12.sđ AC⏜ (góc DBC^ là góc nội tiếp chắn cung AC) ICE^=sđ CA⏜ (góc ICE^ là góc tạo bởi tiếp tuyến IC và dây cung CA)Do đó: IEC^=ICE^⇒IE=ICIEC^+IFC^=90° (ΔFCE vuông tại C)ICE^+ICF^=FCE^=90°mà IEC^=ICE^nên IFC^=ICF^
=>IF=IC
mà IC=IE
nên IF=IC=IE
=>I là tâm đường tròn ngoại tiếp ΔCFE
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13788
Đã trả lời bởi chuyên gia
13788 -
 Đã trả lời bởi chuyên gia
11080
Đã trả lời bởi chuyên gia
11080 -
 Đã trả lời bởi chuyên gia
10106
Đã trả lời bởi chuyên gia
10106 -
 Đã trả lời bởi chuyên gia
8367
Đã trả lời bởi chuyên gia
8367 -
6757
-
 Đã trả lời bởi chuyên gia
6006
Đã trả lời bởi chuyên gia
6006


