cho tam giác abc vuông tại a. Tia phân giác của góc abc cắt ac tại d. kẻ DE vuông góc BC tại E. Chứng minh :
a) tam giác BDA= tam giác BDE và BA = BE
Quảng cáo
2 câu trả lời 1145
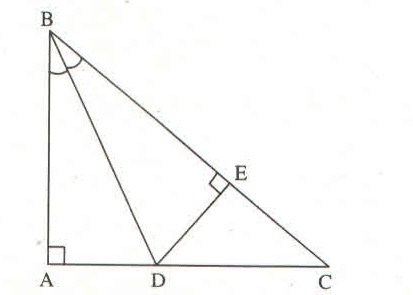
Xét hai tam giác vuông ABD và EBD có:
BD: cạnh chung
góc ABD = góc EBD (BD phân giác)
=> tam giác ABD = tam giác EBD (g.c.g)
=> AB = BE (hai cạnh tương ứng)
Để chứng minh rằng tam giác ( BDA ) đồng dạng với tam giác ( BDE ) và ( BA = BE ), ta sẽ sử dụng các bước sau:
Ta có tam giác ( ABC ) vuông tại ( A ), do đó ( \angle BAC = 90^\circ ).
Tia phân giác của góc ( ABC ) cắt ( AC ) tại ( D ), nên ( \angle ABD = \angle DBC ).
Vì ( DE ) vuông góc với ( BC ) tại ( E ), nên ( \angle BDE = 90^\circ - \angle DBC ).
Từ hai điều trên, ta có ( \angle ABD = \angle BDE ).
Do ( \angle ABD = \angle BDE ) và ( \angle BDA = \angle BDE ) (do cùng thuộc góc ( B )), nên theo góc - góc, ta có ( \triangle BDA ) đồng dạng với ( \triangle BDE ).
Khi hai tam giác đồng dạng, tỉ số các cạnh tương ứng bằng nhau, nên ta có ( \frac{BA}{BD} = \frac{BE}{BD} ) hoặc ( BA = BE ).
Với các bước chứng minh trên, ta đã chứng minh được rằng tam giác ( BDA ) đồng dạng với tam giác ( BDE ) và ( BA = BE ).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8458
Đã trả lời bởi chuyên gia
8458 -
 Đã trả lời bởi chuyên gia
7529
Đã trả lời bởi chuyên gia
7529 -
6460
-
 Đã trả lời bởi chuyên gia
6435
Đã trả lời bởi chuyên gia
6435 -
 Đã trả lời bởi chuyên gia
6264
Đã trả lời bởi chuyên gia
6264 -
 Đã trả lời bởi chuyên gia
6186
Đã trả lời bởi chuyên gia
6186


