Câu 3(2,0 điểm). Cho ∆ABC nhọn có cạnh AB nhỏ hơn cạnh AC. Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC.
a, Chứng minh AAEF = ∆ABC và EF = BC b, Gọi giao điểm của BC và EF là D, chứng minh AD là tia phân giác của góc BAC
Quảng cáo
1 câu trả lời 2323
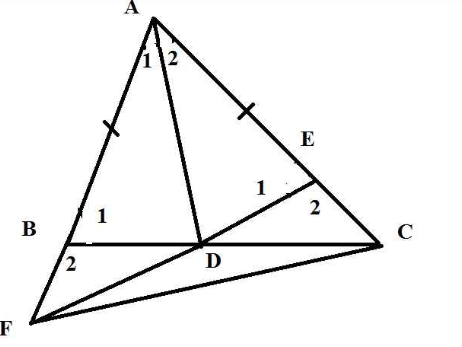
a) Xét ΔAEF và ΔABC có
AE= AB (gt)
góc A: chung
AF=AC (gt)
=> ΔAEF= ΔABC (c.g.c)
=> EF=BC
b)
ΔAEF= ΔABC (câu a)
=> góc AFE = góc ACB
góc BDF= góc EDC (đối đỉnh)
Mà góc B2 = 180 - góc AFE - góc BDF
góc E2 = 180 - góc ABC - góc EDC
=> góc B2 = góc E2
Xét ΔBFD và ΔECD có
góc DBF= góc DEC (cmt)
BF = EC (BF = AF - AB, EC = AC - AE , AF= AC, AB= AE)
góc BFD = góc ECD
=> ΔBFD = ΔECD (g.c.g)
=> BD= ED
Xét ΔABD và ΔAED có
AB=AE
AD: chung
BD=ED (cmt)
=> ΔABD = ΔAED (c.c.c)
=> góc BAD = góc EAD
=> tia AD là phân giác của góc BAC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8458
Đã trả lời bởi chuyên gia
8458 -
 Đã trả lời bởi chuyên gia
7529
Đã trả lời bởi chuyên gia
7529 -
6460
-
 Đã trả lời bởi chuyên gia
6435
Đã trả lời bởi chuyên gia
6435 -
 Đã trả lời bởi chuyên gia
6264
Đã trả lời bởi chuyên gia
6264 -
 Đã trả lời bởi chuyên gia
6186
Đã trả lời bởi chuyên gia
6186


