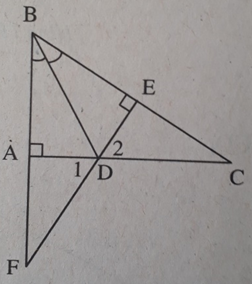
Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: BD là đường thẳng trung trực của AE
Quảng cáo
1 câu trả lời 658
Xét ΔABD và ΔEBD có:
BD chung
∠ABD = ∠EBD ( do BD ,là tia phân giác của góc ABC )
∠BAD = ∠BED = 90º
Suy ra: ΔABD = ΔEBD (cạnh huyền – góc nhọn) ⇒ BA = BE, DA = DE.
Do BA = BE nên B thuộc đường trung trực của AE.
Do DA = DE nên D thuộc đường trung trực của AE.
Do đó BD là đường trung trực của AE.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835
Gửi báo cáo thành công!