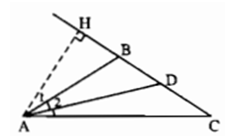
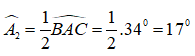Cho tam giác ABC cân tại B có ∠B = 112o. Kẻ đường cao AH và đường phân giác AD của tam giác đó. Tính các góc của tam giác AHD.
Quảng cáo
1 câu trả lời 476
+) Ta có: ∠(ABH) + ∠(ABC) = 180º ( hai góc kề bù)
Suy ra: ∠(ABH) = 180º - ∠(ABC) = 180º − 112º = 68º
+) Xét tam giác AHB vuông tại H ta có:
∠A1+ ∠(ABH) = 90º ( tính chất tam giác vuông)
Suy ra: ∠A1= 90º − ∠(ABH) = 90º − 68º = 22º
+) Tam giác ABC cân tại B nên ∠(BAC) = ∠(ACB)
Lại có ∠(ABC) = 112º và ∠(BAC)+ ∠(ACB) + ∠(ABC) = 180º nên
∠(BAC) = (180º − 112º) : 2 = 34o
+) Do AD là tia phân giác của góc BAC nên
+ Từ đó
∠(HAD) = ∠A1 + ∠A2= 22º + 17º = 39º.
Tam giác HAD vuông tại H nên: ∠(HDA)+ ∠(HAD) = 90º
Suy ra: ∠(HDA) = 90º − ∠(HAD) = 90º − 39º = 51º
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835