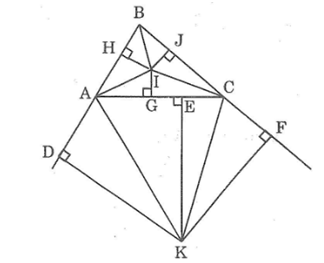
Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.
Quảng cáo
1 câu trả lời 653
Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC
Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)
Vì I nằm trên tia phân giác của ∠(BCA) nên IJ = IG (tính chất tia phân giác)
Suy ra: IH = IJ
Do đó I nằm trên tia phân giác của ∠(ABC) (1)
Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)
Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)
Suy ra: KD = KF
Do đó K nằm trên tia phân giác của ∠(ABC) (2)
Từ (1) và (2) suy ra: B, I, K thẳng hàng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835