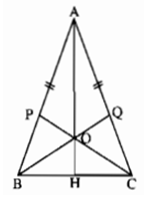
Cho tam giác cân ABC, AB = AC. Trên các cạnh AB, AC lần lượt lấy hai điểm P, Q sao cho AP = AQ. Hai đoạn thẳng CP, BQ cắt nhau tại O. Chứng minh rằng: Tam giác OBC là tam giác cân.
Quảng cáo
1 câu trả lời 549
Ta sẽ chứng minh ΔOBC có hai góc OBC và OCB bằng nhau
ΔABQ và ΔACP có: AB = AC, AQ = AP, ∠A chung
⇒ ΔABQ = ΔACP (c.g.c)
⇒ ∠ABQ = ∠ACP.
Mà ∠ABC = ∠ACB (Vì tam giác ABC cân tại A)
⇒ ∠ABC - ∠ABQ = ∠ACB - ∠ACP hay ∠OBC = ∠OCB
⇒ ΔOBC cân tại O.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835
Gửi báo cáo thành công!