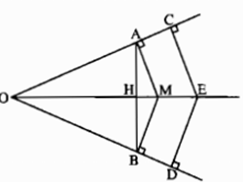
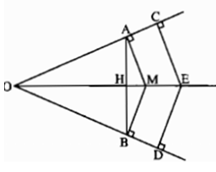
Cho góc đỉnh O khác góc bẹt. Từ một điểm M trên tia phân giác của góc O, kẻ các đường vuông góc MA, MB đến hai cạnh của góc này. Chứng minh rằng AB ⊥ OM.
Quảng cáo
1 câu trả lời 449
Gọi H là giao điểm của AB và OM.
Xét ΔAOM (vuông tại A) và ΔBOM (vuông tại B) có:
OM chung
∠MOA = ∠MOB ( vì OM là tia phân giác của góc xOy)
⇒ ΔAOM = ΔBOM (cạnh huyền – góc nhọn)
⇒ OA = OB.
+) Xét ΔOAH và ΔBOH có:
OA = OB ( chứng minh trên )
OH chung
∠AOH = ∠BOH ( vì OH là tia phân giác của góc xOy)
⇒ ΔOAH = ΔOBH (c.g.c)
⇒ ∠OHA = ∠OHB. Mà ∠OHA + ∠OHB = 180o ( hai góc kề bù)
⇒ ∠OHA = ∠OHB = 90o
Vậy AB ⊥ OM.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835
Gửi báo cáo thành công!