Chứng minh “Bất đẳng thức tam giác mở rộng ”: Với ba điểm A, B, C bất kỳ, ta có AB + AC ≥ BC
Quảng cáo
1 câu trả lời 622
- Nếu A, B, C không thẳng hàng thì 3 điểm A, B, C tạo thành 3 đỉnh của 1 tam giác.
Trong tam giác ABC ta có AB + AC > BC
- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC
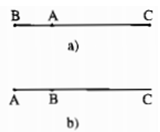
• Nếu A nằm giữa B và C thì AB + AC = BC.
• Nếu B nằm giữa A và C thì AB + BC = AC nên AC > BC.
Suy ra: AC + AB > BC
• Nếu C nằm giữa A và B thì AC + CB = AB nên AB > BC.
Suy ra: AB + AC > BC.
Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835
Gửi báo cáo thành công!