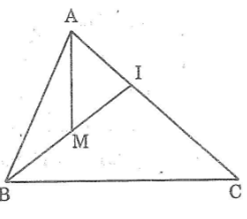
Cho hình bên. Chứng minh rằng: MA + MB < IA + IB < CA + CB
Quảng cáo
1 câu trả lời 476
Trong ΔAMI ta có:
MA < MI + IA
(theo bất đẳng thức tam giác)
Cộng vào hai vế với MB ta có:
MA + MB < MI + IA + MB
⇒ MA + MB < IB + IA (1)
Trong ΔBIC, ta có:
IB < IC + CB (bất đẳng thức tam giác)
Cộng vào 2 vế với IA ta có:
IB + IA < IC + CB + IA
⇒ IB + IA < CA + CB (2)
Từ (1) và (2) suy ra: MA + MB < IA + IB < CA + CB.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835
Gửi báo cáo thành công!