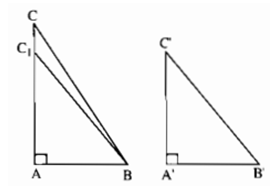
Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lý Pitago, chứng minh rằng BC > B'C'
Quảng cáo
1 câu trả lời 363
Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′. Ta có tam giác vuông ABC1 bằng tam giác vuông A'B'C', suy ra B′C′=BC1. Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1. Vì AC > AC1 nên BC > BC1. Suy ra BC > B'C'.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835
Gửi báo cáo thành công!