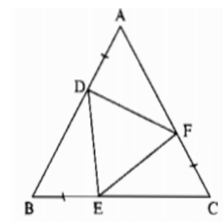
Cho tam giác đều ABC. Lấy các điểm D, E , F theo thứ tự thuộc các cạnh AB, BC và CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều?
Quảng cáo
1 câu trả lời 853
Ta có: AB = AD +DB (1)
BC = BE + EC (2)
AC = AF + FC (3)
AB = AC = BC ( vì tam giác ABC là tam giác đều) (4)
AD = BE = CF ( giả thiết) (5)
Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF
Xét ΔADF và ΔBED, ta có:
AD = BE (gt)
∠A =∠B =60o (vì tam giác ABC đều)
AF = BD (chứng minh trên)
suy ra: ΔADF= ΔBED (c.g.c)
⇒ DF=ED (hai cạnh tương ứng) (6)
Xét ΔADF và ΔCFE, ta có:
AD = CF (gt)
∠A =∠C =60o (vì tam giác ABC đều)
AF = CE (chứng minh trên)
suy ra: ΔADF= ΔCFE (c.g.c)
Nên: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy tam giác DFE đều
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12381
-
 Đã trả lời bởi chuyên gia
5734
Đã trả lời bởi chuyên gia
5734 -
4829