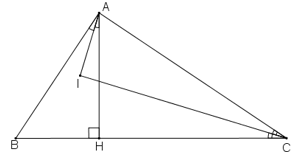
Cho tam giác ABC có ∠A=90o, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác của ∠C và ∠BAH cắt nhau ở I. Chứng minh rằng: ∠(AIC)=90o
Quảng cáo
1 câu trả lời 2310
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12381
-
 Đã trả lời bởi chuyên gia
5734
Đã trả lời bởi chuyên gia
5734 -
4829