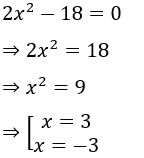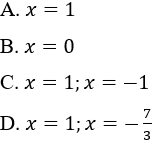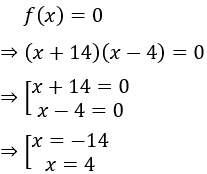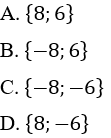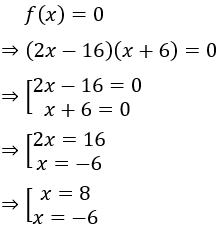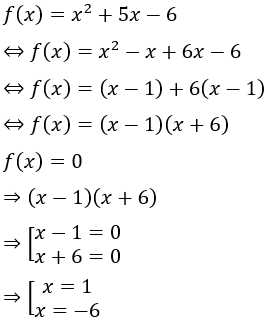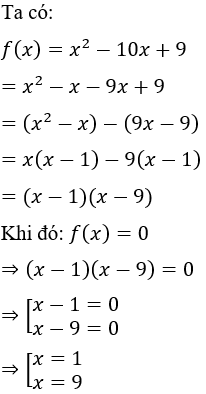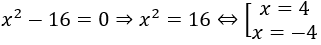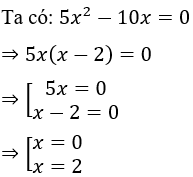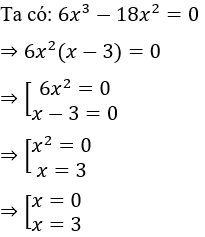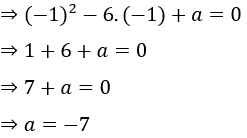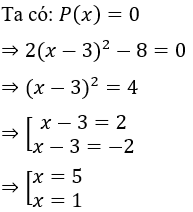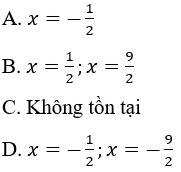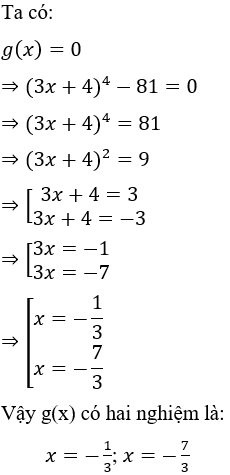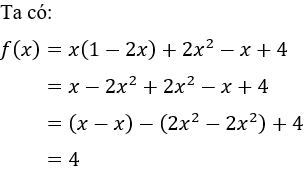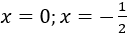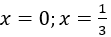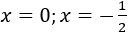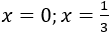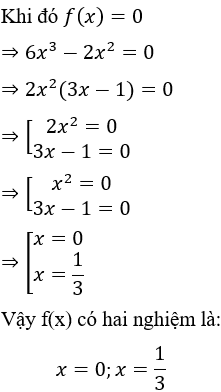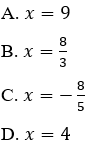Trắc nghiệm Toán học 7 Nghiệm của đa thức một biến 

Câu 1: Hiệu giữa nghiệm lớn và nghiệm nhỏ của đa thức 2x² - 18 là:

A. 6

B. 18

C. -6

D. 0

Lời giải:

Ta có:

Vậy x = 3;x = -3  là nghiệm của đa thức 2x² - 18

Hiệu giữa nghiệm lớn và nghiệm nhỏ của đa thức 2x² - 18 là 3-(-3) = 6

Đáp án cần chọn là: A

Câu 2: Cho đa thức sau f(x) = 2x² + 5x + 2. Trong các số sau, số nào là nghiệm của đa thức đã cho:  

A. 2

B. 1

C. -1

D. -2

Lời giải:

f(2) = 2.2² + 5.2 + 2 = 20 ≠ 0 ⇒ x = 2 không là nghiệm của f(x)

f(1) = 2.1² + 5.1 + 2 = 9 ≠ 0 ⇒ x = 1 không là nghiệm của f(x)

f(-1) = 2.(-1)² + 5.(-1) + 2 = -1 ≠ 0 ⇒ x = -1 không là nghiệm của f(x)

f(-2) = 2.(-2)² + 5.(-2) + 2 = 0 ⇒ x = -2 là nghiệm của f(x)

Đáp án cần chọn là: D

Câu 3: Cho các giá trị của x là 0;-1;1;2;-2. Gía trị nào của x là nghiệm của đa thức P(x) = x² + x - 2

A. x = 1; x = -2

B. x = 0; x = -1; x = -2

C. x = 1; x = 2

D. x = 1; x = -2; x = 2

Lời giải:

P(0) = (0)² + 1.0-2=-1 ≠ 0 ⇒ x = 0 không là nghiệm của P(x)

P(-1) = (-1)² + 1.(-1)-2=-2 ≠ 0 ⇒ x = -1 không là nghiệm của P(x)

P(1) = 1² + 1.1-2 = 0 ⇒ x = 1 là nghiệm của P(x)

P(2) = 2² + 1.2-2=4 ≠ 0 ⇒ x = 2 không là nghiệm của P(x)

P(-2) = (-2)² + 1.(-2)-2 = 0 ⇒ x = -2 là nghiệm của P(x)

Vậy x = 1;x = -2 là nghiệm của P(x)

Đáp án cần chọn là: A

Câu 4: Cho các giá trị của x là 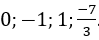. Gía trị nào của x là nghiệm của đa thức P(x) = 3x² - 10x+7

Lời giải:

P(0) = 3.0² - 10.0+7=7 ≠ 0 ⇒ x = 0 không là nghiệm của P(x)

P(-1) = 3.(-1)² - 10.(-1)+7=20 ≠ 0 ⇒ x = -1 không là nghiệm của P(x)

P(1) = 3.(1)² - 10.(1)+7 = 0 ⇒ x = 1 là nghiệm của P(x)

 không là nghiệm của P(x)

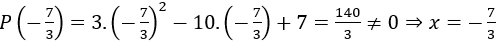
Vậy x = 1  là nghiệm của P(x)

Đáp án cần chọn là: A

Câu 5: Tập nghiệm của đa thức  f(x) = (x + 14)(x-4) là:

A. {4;14}

B. {-4;14}

C. {-4; -14}

D. {4; -14}

Lời giải:

Vậy tập nghiệm của đa thức f(x) là {4; -14}

Đáp án cần chọn là: D

Câu 6: Tập nghiệm của đa thức f(x) = (2x - 16)(x+6)  là:

Lời giải:

Vậy tập nghiệm của đa thức f(x) là {8;-6}

Đáp án cần chọn là: D

Câu 7: Cho đa thức sau: f(x) = x² + 5x - 6. Các nghiệm của đa thức đã cho:

A. 2 và 3

B. 1 và -6

C. -3 và -6

D. -3 và 8

Lời giải:

Vậy nghiệm của đa thức f(x) là 1 và -6

Đáp án cần chọn là: B

Câu 8: Cho đa thức sau: f(x) = x² - 10x+9. Các nghiệm của đa thức đã cho:

A. 4 và 6

B. 1 và 9

C. -3 và -7

D. 2 và 8

Lời giải:

Vậy nghiệm của đa thức f(x) là 1 và 9

Đáp án cần chọn là: B

Câu 9: Tổng các nghiệm của đa thức x² - 16 là:

A. -16

B. 8

C. 4

D. 0

Lời giải:

Vậy =4;x = -4 là nghiệm của đa thức x² - 16

Tổng các nghiệm là 4 + (-4) = 0

Đáp án cần chọn là: D

Câu 10: Cho đa thức sau f(x) = 2x² + 12x + 10. Trong các số sau, số nào là nghiệm của đa thức đã cho:   

A. -9

B. 1

C. -1

D. -4

Lời giải:

f(-9) = 2.9² + 12.9+10=64 ≠ 0 ⇒ x = -9 không là nghiệm của f(x)

f(1) = 2.1² + 12.1+10=24 ≠ 0 ⇒ x = 1 không là nghiệm của f(x)

f(-1) = 2.1² + 12.(-1)+10 = 0 ⇒ x = -1 là nghiệm của f(x)

f(-4) = 2.(-4)² + 12.(-4)+10=-6 ≠ 0 ⇒ x = -4 không là nghiệm của f(x)

Đáp án cần chọn là: C

Câu 11: Số nghiệm của đa thức x³ + 27

A. 1

B. 2

C. 0

D. 3

Lời giải:

Ta có: x³ + 27 = 0 ⇒ x³ = -27 ⇒ x³ = (-3)³ ⇒ x = -3

Vậy đa thức đã cho có một nghiệm là x = -3

Đáp án cần chọn là: A

Câu 12: Số nghiệm của đa thức x³ - 64 là:

A. 1

B. 2

C. 4

D. 3

Lời giải:

Ta có: x³ - 64 = 0 ⇒ x³ = 64 ⇒ x³ = 4³ ⇒ x = 4

Vậy đa thức đã cho có một nghiệm là x = 4

Đáp án cần chọn là: A

Câu 13: Tích các nghiệm của đa thức 5x² - 10x là

A. -2

B. 2

C. 0

D. 4

Lời giải:

Vậy đa thức 5x² - 10 có hai nghiệm x = 0 hoặc x = -2

Tích các nghiệm là 0.(-2) = 0

Đáp án cần chọn là: C

Câu 14: Tích các nghiệm của đa thức 6x³ - 18x² là:

A. -3

B. 3

C. 0

D. 9

Lời giải:

Vậy đa thức 6x³ - 18x² có hai nghiệm x = 0 hoặc x = 3

Tích các nghiệm của đa thức 6x³ - 18x² là 0.3 = 0

Đáp án cần chọn là: C

Câu 15: Cho đa thức f(x) = ax² + bx + c. Chọn câu đúng?

A. Nếu a + b + c = 0 thì đa thức f(x) có một nghiệm x = 1

B. Nếu a - b + c = 0 thì đa thức f(x) có một nghiệm x = -1

C. Cả A và B đều đúng

D. Cả A và B đều sai

Lời giải:

+ Với a + b + c = 0 thay x = 1 vào f(x) ta được

f(1) = a.1² + b.1 + c = a + b + c ⇒ f(1) = 0

Nên x = 1 là một nghiệm của đa thức f(x)

+ Với a - b + c = 0 thay x = -1 vào f(x) ta được

f(-1) = a.(-1)² + b.(-1)+c = a - b + C ⇒ f(-1) = 0

Nên x = -1 là một nghiệm của đa thức f(x)

Vậy cả A, B đều đúng

Đáp án cần chọn là: C

Câu 16: Cho đa thức f(x) = ax³ + bx² + cx+d. Chọn câu đúng?

A. Nếu a + b + c + d = 0 thì đa thức f(x) có một nghiệm x = 1

B. Nếu a - b + c - d = 0 thì đa thức f(x) có một nghiệm x = -1

C. Cả A và B đều đúng

D. Cả A và B đều sai

Lời giải:

+ Với a + b + c + d = 0 thay x = 1 vào f(x) = ax³ + bx² + cx + d ta được

f(1) = a.1³ + b.1² + c.1+d = a + b + c + d ⇒ f(1) = 0

Vậy x = 1 là một nghiệm của đa thức f(x)

+ Với a - b + c - d = 0 thay x = -1 vào f(x) = ax³ + bx² + cx + d ta được

f(-1) = a.(-1)³ + b.(-1)² + c.(-1)+d = -a + b - c + d = -(a-b + c-d) = 0 ⇒ f(-1) = 0

Nên x = -1 là một nghiệm của đa thức f(x)

Vậy cả A, B đều đúng

Đáp án cần chọn là: C

Câu 17: Cho P(x) = x² - 6x + a. Tìm a để P(x) nhận -1 là nghiệm

A. a = 1

B. a = -7

C. a = 7

D. a =  6

Lời giải:

P(x) nhận -1 là nghiệm nên P(-1) = 0

Vậy P(x) nhận -1 là nghiệm thì a = -7

Đáp án cần chọn là: B

Câu 18: Cho Q(x) = ax² - 2x - 3. Tìm a để Q(x) nhận 1 là nghiệm

A. a = 1

B. a = -5

C. a = 5

D. a = -1

Lời giải:

Q(x) nhận  1 là nghiệm thì Q(1) = 0

⇒ a.1² - 2.1-3 = 0 ⇒ a-5 = 0 ⇒ a = 5

Vậy để Q(x) nhận  1 là nghiệm thì a = 5

Đáp án cần chọn là: C

Câu 19: Đa thức f(x) = x² - x + 1 có bao nhiêu nghiệm ?

A. 1

B. 0

C. 2

D. 3

Lời giải:

+ Xét x < 0 khi đó x - 1 < 0 nên x(x-1) > 0 do đó x² - x + 1 > 0

Hay f(x) > 0

+ Xét 0 ≤ x < 1 khi đó x²> 0 và 1 - x > 0 do đó

x² + (1-x) = x² - x + 1>0nên f(x) > 0

+ Xét x ≥ 1thì x > 0 và x(x-1) ≥ 0 suy ra x² - x + 1>0 hay f(x) > 0

Vậy f(x) > 0 với mọi x nên f(x) vô nghiệm

Đáp án cần chọn là: B

Câu 20: Đa thức f(x) = 2x² - 2x + 3 có bao nhiêu nghiệm ?

A. 1

B. 0

C. 2

D. 3

Lời giải:

Ta có:

f(x) = 2x² - 2x + 3=x² + x² - x-x + 1 + 2

= x² + (x² - x) - (x-1) + 2 = x² + x(x-1) - (x-1) + 2

= x² + (x-1)(x-1) + 2 = x² + (x-1)² + 2

Với mọi x ta có : x² ≥ 0;(x-1)² ≥ 0

Mặt khác 2 > 0 nên x² + (x-1)² + 2>0 với mọi x hay f(x) > 0 với mọi x

Do đó f(x) không có nghiệm

Đáp án cần chọn là: B

Câu 21: Biết (x-1)f(x) = (x + 4)f(x+8). Khi đó đa thức f(x) có ít nhất là bao nhiêu nghiệm?

A. 2

B. 1

C. 3

D. 4

Lời giải:

Vì (x-1)f(x) = (x + 4)f(x+8) với mọi x nên suy ra:

+ Khi x - 1 = 0, hay x = 1 thì ta có:

(1-1)f(1) = (1+4)f(1+8) ⇒ 0f(1) = 5.f(9) ⇒ f(9) = 0

Vậy x = 9 là một nghiệm của f(x)

+ Khi x + 4 = 0 hay x = -4 ta có:

(-4-1)f(-4) = (-4+4)f(-4+8) ⇒ -5.f(-4) = 0.f(4) ⇒ f(-4) = 0

Vậy x = -4 là một nghiệm của f(x)

Vậy f(x) có ít nhất 2 nghiệm là 9 và -4

Đáp án cần chọn là: A

Câu 22: Biết x.f(x + 1) = (x + 3).f(x). Khi đó đa thức f(x) có ít nhất là bao nhiêu nghiệm?

A. 2

B. 1

C. 3

D. 4

Lời giải:

Ta có: x.f(x + 1) = (x + 3).f(x) với mọi x

+ Khi x = 0 ta có:

0.f(0+1) = (0 + 3).f(0) ⇒ 0.f(1) = 3.f(0) ⇒ f(0) = 0

Vậy x = 0 là một nghiệm của f(x)

+ Khi x + 3 = 0 hay x = -3 ta có:

(-3).f(-3+1) = (-3 + 3).f(-3) ⇒ (-3).f(-2) = 0.f(-3) ⇒ f(-2) = 0

Vậy x = -2 là một nghiệm của f(x)

Vậy f(x) có ít nhất 2 nghiệm là 0 và -2

Đáp án cần chọn là: A

Câu 23: Nghiệm của đa thức P(x) = 2(x - 3)² - 8  là

A. x = 0

B. x = 5; x = -1

C. Không tồn tại

D. x = 5; x = 1

Lời giải:

Vậy đa thức P(x) có hai nghiệm x = 5; x = 1

Đáp án cần chọn là: D

Câu 24: Nghiệm của đa thức P(x) = 3(2x+5)² - 48 là

Lời giải:

Đáp án cần chọn là: D

Câu 25: Số nghiệm của đa thức g(x) = (3x + 4)⁴ - 81  là

A. 0

B. 1

C. 2

D. 4

Lời giải:

Đáp án cần chọn là: C

Câu 26: Thu gọn rồi tìm nghiệm của đa thức sau: f(x) = x(1-2x) + 2x² - x + 4

A. f(x) = 4x² + 4 ; f(x) không có nghiệm

B. f(x) = -2x + 4 ; f(x) có nghiệm là x = 2

C. f(x) = 4 ; f(x) không có nghiệm

D. f(x) = 4 ; f(x) có nghiệm là x = 4

Lời giải:

Vì f(x) = 4 > 0 với mọi x nên f(x) không có nghiệm

Đáp án cần chọn là: C

Câu 27: Tìm đa thức f(x) rồi tìm của đa thức f(x) biết nhanh:

x³ + 2x² (4y-1)-4xy² - 9y³ - f(x) = -5x³ + 8x²y - 4xy² - 9y³

A. f(x) = - 4x³ - 2x² ; f(x)  có nghiệm là 

B. f(x) = 6x³ - 3x² ; f(x) có nghiệm là 

C. f(x) = 4x³ + 3x² ; f(x) có nghiệm 

D. f(x) = -6x³ + 2x² ; f(x) có nghiệm là 

Lời giải:

Ta có:

x³ + 2x² (4y-1)-4xy² - 9y³ - f(x) = -5x³ + 8x²y - 4xy² - 9y³

⇒ f(x) = [x³ + 2x² (4y-1)-4xy² - 9y³]-(-5x³ + 8x²y - 4xy² - 9y³)

= x³ + 8x²y - 2x² - 4xy² - 9y³ + 5x³ - 8x²y + 4xy² + 9y³

= (x³ + 5x³) + (8x²y-8x²y) - 2x² + (-4xy² + 4xy²) + (-9y³ + 9y³)

= 6x³ - 2x²

Đáp án cần chọn là: B

Câu 28: Cho f(x) = 2x² (x-1)-5(x + 2)-2x(x - 2); g(x) = x² (2x - 3)-x(x + 1) - (3x - 2)

28.1: Thu gọn f(x); g(x) theo lũy thừa giảm dần của biến

A. f(x) = 2x³ - 2x² - 3x - 10; g(x) = 2x³ - 4x² - 4x + 2

B. f(x) = 2x³ - 4x² - x - 10; g(x) = 2x³ - 4x² - 4x + 2

C. f(x) = 2x³ + 4x² - x - 10; g(x) = 2x³ + 2x² - 4x + 2

D. f(x) = 2x³ - 4x² - x - 10; g(x) = 2x³ + 2x² + 4x + 2

Lời giải:

Ta có:

f(x) = 2x² (x-1)-5(x + 2)-2x(x - 2)

 = (2x³ - 2x²) - (5x + 10) - (2x² - 4x)

 = 2x³ - 2x² - 5x - 10 - 2x² + 4x

 = 2x³ + ( - 2x² - 2x²) + (-5x-4x)-10

 = 2x³ - 4x² - 9x - 10

g(x) = x² (2x - 3)-x(x + 1) - (3x - 2)

 = (2x³ - 3x²) - (x² + x) - (3x - 2)

 = 2x³ - 3x² - x² - x - 3x + 2

 = 2x³ - (3x² + x²) + (-x - 3x) + 2

 = 2x³ - 4x² - 4x + 2

Sắp xếp f(x); g(x) theo lũy thừa giảm dần của biến ta được

f(x) = 2x³ - 4x² - x - 10; g(x) = 2x³ - 4x² - 4x + 2

Đáp án cần chọn là: B

Lời giải:

 Theo câu trước ta có:

f(x) = 2x³ - 4x² - x - 10; g(x) = 2x³ - 4x² - 4x + 2

Khi đó:

h(x) = f(x) - g(x)

= 2x³ - 4x² - x - 10-(2x³ - 4x² - 4x + 2)

= 2x³ - 4x² - x - 10 - 2x³ + 4x² + 4x - 2

= (2x³ - 2x³) + ( - 4x² + 4x²) + (-x + 4x) + (-10-2)

= 3x-12

Đáp án cần chọn là: A

28.3 : Tính nghiệm của h(x) biết h(x) = f(x) - g(x)

Lời giải:

Theo câu trước ta có: h(x) = 3x - 12

Khi đó h(x) = 0 ⇒ 3x - 12 = 0 ⇒ 3x = 12 ⇒ x = 4

Vậy nghiệm của h(x) là x = 4

Đáp án cần chọn là: D