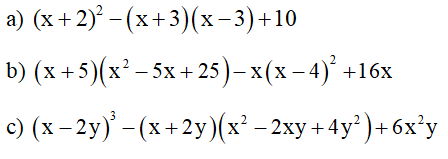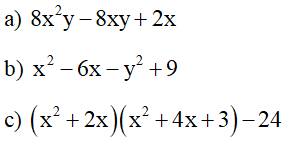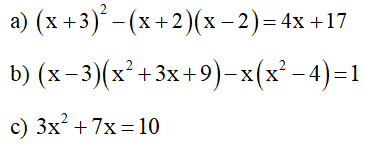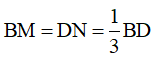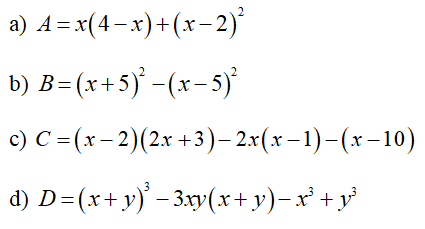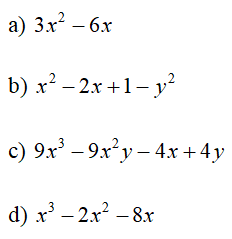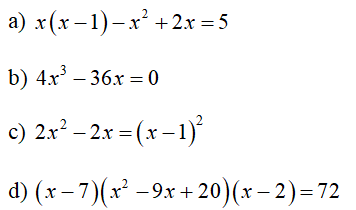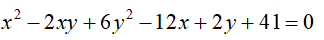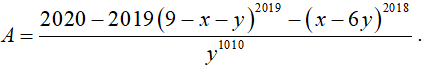Bộ 30 đề thi Giữa học kì 1 Toán lớp ́8 có đáp án
Bộ 30 đề thi Giữa học kì 1 Toán lớp 8 Kết nối tri thức có đáp án giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 8 Giữa học kì 1. Mời các bạn cùng đón xem:
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 1)
Bài 1 (2 điểm). Phân tích đa thức thành nhân tử:
![]()
Bài 2 (1,5 điểm). Sắp xếp và thực hiện phép chia:
Bài 3 (2 điểm). Tìm , biết:
a)
b)
Bài 4 (3,5 điểm). Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Lấy một điểm E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF.
a) Chứng minh tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành.
b) Gọi H và K lần lượt là hình chiếu của F trên các đường thẳng BC và CD. Chứng minh tứ giác CHFK là hình chữ nhật.
c) Chứng minh bốn điểm E, H, K, I thẳng hàng.
Bài 5 (1 điểm). Tìm giá trị lớn nhất của biểu thức:
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 2)
Bài 1. Rút gọn:
a)
b)
c) ![]()
Bài 2. Phân tích các đa thức sau thành nhân tử:
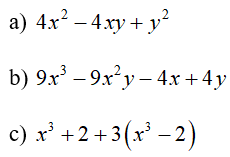
Bài 3.
1) Tìm x biết
2) Chứng minh rằng với bất kì bộ ba số tự nhiên liên tiếp nào thì tích của số thứ nhất và số thứ ba cũng bé hơn bình phương của số thứ hai 1 đơn vị.
Bài 4. Cho tam giác ABC có ba góc nhọn (AB < AC), đường cao AH. M, N, P lần lượt là trung điểm của AB, AC và BC. I là giao điểm của AH và MN.
a) Chứng minh MN là đường trung trực của AH.
b) Kéo dài PN một đoạn NQ = NP. Xác định dạng tứ giác ABPQ.
c) Xác định dạng tứ giác MHPN.
d) K là trung điểm của MN. Chứng minh B, K, Q thẳng hàng.
Bài 5.Tìm giá trị nhỏ nhất của biểu thức .
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 3)
Bài 1 : (2 điểm) Rút gọn các biểu thức:
Bài 2 : (2,0 điểm) Phân tích đa thức thành nhân tử:
Bài 3 : (2 điểm) Tìm x, biết:
Bài 4 : (3 điểm) Cho hình bình hành ABCD. Trên đường chéo BD lấy 2 điểm M và N sao cho
a) Chứng minh rằng: ΔAMB = ΔCND
b) AC cắt BD tại O. Chứng minh tứ giác AMCN là hình bình hành.
c) AM cắt BC tại I. Chứng minh: AM = 2MI
d) CN cắt AD tại K. Chứng minh: I và K đối xứng với nhau qua O
Bài 5 : (1 điểm)
a) Tìm GTLN của biểu thức: A = 5 + 2xy + 14y - x2 - 5y2 - 2x
b) Tìm tất cả số nguyên dương n sao cho B = 2n + 3n + 4n là số chính phương.
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 4)
Câu 1 :
Câu 2 : Phân tích đa thức thành nhân tử:
a) (x - 4)2 - 9
b) 5x + 5y - x2 - 2xy - y2
c) X2 + 4x - 5
d) x4 + 4
Câu 3 : Tìm x biết:
a) 5(x + 2) + x(x + 2) = 0
b) (3x - 1)2 - 9x2 + 3 = 0
c) (x + 3)(x2 - 3x + 9) - x(x2 - 9) = 27
Câu 4 : Cho hình bình hành MNPQ (MN > PQ) . Lấy điểm A trên canh MN , điểm B trên cạnh PQ sao cho AM = BP
a) Chứng minh rằng: MB // AP ,MB = AP .
b) Chứng minh rằng MB , NQ , AB đồng quy tại một điểm I .
c) Gọi H là giao điểm của MB và NQ . Tìm vị trí của A , B trên 2 cạnh MN , PQ của hình bình hành MNPQ để H là trọng tâm của tam giác MPQ .
d) Gọi C là giao điểm của 2 đường phân giác góc 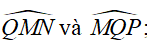
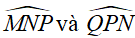
Câu 5 :
a) Cho a , b , c > 0 thỏa mãn a2020 + b2020 + c2020 = a1010b1010 + b1010c1010 + c1010a1010 . Tính giá trị của biểu thức sau A = (a - b)20 +(b - c)33 + (c - a)2020
b) Chúng minh rằng với mọi x ∈ Q thì giá trị của biểu thức A = (x + 1)(x + 2)(x + 3)(x + 4) + 1 là bình phương của một số hữu tỷ?
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 5)
Câu 1 : Phân tích các đa thức sau thành nhân tử:
Câu 2 : Tìm x , biết:
Câu 3 :
a) Thực hiện phép tính chia đa thức sau:
f(x) = 2x4 - 3x3 + 3x -2 cho đa thức g(x) = x2 -1
b) Cho hai đa thức A(x) = 2x3 + 3x2 - x + m và B(x) = 2x + 1
Tìm m để A(x) chia hết cho B(x) .
Câu 4 : Cho tam giác ABC có ba góc nhọn (AB < AC) , đường cao AH Gọi M,N,P lần lượt là trung điểm của các cạnh AB, AC, BC, MN, cắt AH tại I
a) Chứng minh I là trung điểm của AH
b) Lấy điểm Q đối xứng với P qua N Chứng minh tứ giác ABPQ là hình bình hành.
c) Xác định dạng của tứ giác MHPN
d) Gọi K là trung điểm của MN , O là giao điểm của CK và PQ , F là giao điểm của MN và QC Chứng minh B,O,F thẳng hàng.
Câu 5 : Cho các số x,y thỏa mãn điều kiện
Tính giá trị biểu thức
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 6)
I. PHẦN TRẮC NGHIỆM (2 ĐIỂM)
Câu 1. Khai tiển biểu thức x3-8x3 ta được kết quả là:
A. (x-2y)3
B. x3-2y3
C. (x-2y)(x2+2xy+4y2)
D. x3-6x2y + 12xy2-8y3
Câu 2. Kết quả phép tính -x2(3-2x)là:
A. 3x2-2x3
B.2x3-3x2
C.-3x3+2x2
D.-4x2
Câu 3. Để 4y2-12y + trở thành một hằng đảng thức. Giá trị trong ô vuông là:
trở thành một hằng đảng thức. Giá trị trong ô vuông là:
A. 6
B. 9
C. – 9
D. Một kết quả khác
Câu 4. Biểu thức 1012 – 1 có giá trị bằng
A. 100
B. 1002
C. 102000
D. Một kết quả khác
Câu 5. Giá trị của biểu thức x2+2xy+y2 tại x = - 1 và y = - 3 bằng
A. 16
B. – 4
C. 8
D. Một kết quả khác
Câu 6. Biết 4x(x2-25)=0, các số x tìm được là:
A. 0; 4; 5
B. 0; 4
C. -5; 0; 5
D. Một kết quả khác
Câu 7.
A. -2x +4 =2(2-x)
B. -2x+4 = -2(2-x)
C. -2x +4= -2(x+2)
D. -2x+4= 2(x-2)
Câu 8. Thực hiện phép nhân x(x-y)
A.x2-y
B.x-xy
C.x-x2
D.x2-xy
II. PHẦN TỰ LUẬN (8 ĐIỂM)
Bài 1 (1,5đ): Phân tích các đa thức sau thành nhân tử
a. 36a4-y2
b. 6x2 +x -2
Bài 2 (1,5đ). Tìm x, biết:
a. x( x-4)+1 = 3x-5
b. 2x3-3x2-2x+3= 0
Bài 3 (1,5đ).
a. Cho biểu thức A= x3-9x2+27x -27 . Tính giá trị của A khi x = 1.
b. Tìm đa thức thương và đa thức dư trong phép chia đa thức A (x) cho B (x). Biết:
A(x)= 2x3+x2-x+ a và B(x) = x-2
Bài 4 (3,0đ). Cho hình bình hành ABCD có AB > BC. Đường phân giác của góc cắt AB tại M, đường phân giác của góc cắt CD tại N.
a. Chứng minh AM = CN.
b. Chứng minh tứ giác DMBN là hình bình hành.
c. Gọi H, K lần lượt là hình chiếu của N và N trên BN và DM. Chứng minh hai đoạn thẳng AC và MN cắt nhau tại trung điểm của mỗi đường.
Bài 5 (0,5đ). Tìm giá trị lớn nhất của biểu thức:
A = -2x2 -10y2 +4xy +4x+ 4y +2016
Đáp án đề thi Giữa kì 1 môn Toán 8 - Đề số 6
I. PHẦN TRẮC NGHIỆM
Câu 1: C (0,25đ)
Câu 2: B (0,25đ)
Câu 3: B (0,25đ)
Câu 4: C (0,25đ)
Câu 5: A (0,25đ)
Câu 6: C (0,25đ)
Câu 7: A (0,25đ)
Câu 8: D (0,25đ)
II. PHẦN TỰ LUẬN (8 ĐIỂM)
Bài 1
a. 36a4-y2= (6a)2-y2= (6a-y)(6a+y)
b.6x2 +x -2 = 6x2+4x -3x -2
= 2x( 3x+2) - (3x+2) = (2x-1)(3x+2)
Bài 2
a. x(x-4) +1 = 3x-5
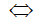 x(x-1) - 6(x-1)=0 (0,25đ)
x(x-1) - 6(x-1)=0 (0,25đ)
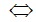 (x-1)(x-6)=0 (0,25đ)
(x-1)(x-6)=0 (0,25đ)
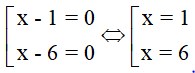
Vậy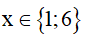 là giá trị cần tìm.
là giá trị cần tìm.
b. 2x3-3x2-2x+3= 0
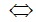 x2( 2x-3) -(2x-3) =0
x2( 2x-3) -(2x-3) =0
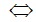 (2x-3)(x2-1) =0
(2x-3)(x2-1) =0
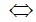 (2x-3)(x-1)(x+1)=0
(2x-3)(x-1)(x+1)=0
 .....
.....
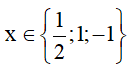
Vậy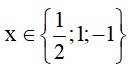 là giá trị cần tìm.
là giá trị cần tìm.
Bài 3
a. Xét biểu thức:
A= x3-9x2+27x -27
= x3 -3.x2.3 +3.x.32- 33
=(x-3)3
Với x = 1 biểu thức A được viết lại như sau:
A=(1-3)3 = -8
Vậy A = - 8 khi x = 1
b.Thực hiện đúng được phép chia A(x)= 2x3+x2-x+ a cho B(x) = x-2, tìm được thương bằng:2x2+5x +9 và dư bằng a + 18. (1,0đ)
Bài 4
Vẽ đúng hình
a. Chứng minh được AM = CN
b. Chứng minh được tứ giác DMBN là hình bình hành
c. Lập luận chặt chẽ chỉ ra được hai đoạn thẳng AC và MN cắt nhau tại trung điểm của mỗi đường
Bài 5
A = -2x2 -10y2 +4xy +4x+ 4y +2016
=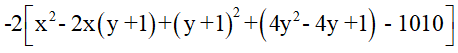
= -2( x-y-1)2 -2(2y-1)2 +2020
GTLN của A bằng 2020 khi 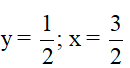
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 7)
A. TRẮC NGHIỆM (3 điểm).
1) Tích của đơn thức x2 và đa thức 5x3 -x-1 là:
A. 5x6-x3-x2
B. -5x5+ x3 +x2
C. 5x5-x3-x2
D. 5x5-x-1
2) Đa thức 3x2-12 được phân tích thành nhân tử là:
A. 3x(x-2)2
B. 3x( x2+4)
C. 3(x - 2)(x + 2)
D. x(3x - 2)(3x + 2)
3) Cho tứ giác ABCD biết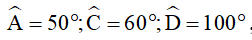 khi đó số đo góc B là
khi đó số đo góc B là
A. 1500
B. 1050
C. 750
D. 300
4) Đa thức x4-3x3+6x2-7x+m chia hết cho đa thức x - 1 khi m bằng
A. 0
B. - 3
C. 3
D. 1
5) Giá trị nhỏ nhất của đa thức A= x2+4x+11 là
A. 7
B. - 2
C. - 4
D. 11
6) Cho tam giác ABC vuông tại A, O là trung điểm của BC. D là điểm đối xứng với A qua O. Đẳng thức nào sai trong các đẳng thức sau?
A.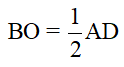
B.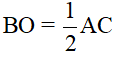
C. AB = CD
D. AD = BCB. TỰ LUẬN
Câu 1 (2 điểm)
1) Tìm x biết x(x – 1) + x – 1 = 0
2) Tính giá trị biểu thức: A= (x-y)(x2+xy+y2) +2y2tại 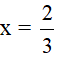 và
và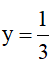
Câu 2 (2 điểm) Cho đa thức A= 2x4 + 3x3 - 4x2 -3x +2 và đa thức B = x + 2
1) Làm tính chia đa thức A cho đa thức B.
2) Hãy phân tích đa thức thương của phép chia đa thức A cho đa thức B thành nhân tử.
Câu 3 (2,5 điểm) Cho hình bình hành ABCD trong đó có BC = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.
1) Chứng minh rằng tứ giác MNDC là hình bình hành.
2) Kẻ DE vuông góc với AB tại E, DE cắt MN tại F. Chứng minh F là trung điểm của DE.
3) Chứng minh rằng: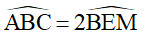
Câu 4 (0,5 điểm) Cho các số x, y, z thỏa mãn đồng thời:
x+ y+ z= 1; x2+y2+z2= 1; x3 + y3+z3 =1
Tính giá trị của biểu thức: M= x8+y11+ z2018
Đáp án đề thi Giữa kì 1 môn Toán 8 - Đề số 7
A. TRẮC NGHIỆM (3 ĐIỂM)
Câu 1: C (0,5đ)
Câu 2: C (0,5đ)
Câu 3: A (0,5đ)
Câu 4: C (0,5đ)
Câu 5: A (0,5đ)
Câu 6: B (0,5đ)
B. TỰ LUẬN (7 điểm)
Câu 1
1) x(x – 1) + x – 1 = 0
=> (x - 1)(x + 1) = 0
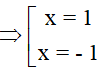
Vậy 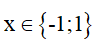
2) A= (x-y)(x2+xy+y2) +2y2
= x3 + y3
Tại 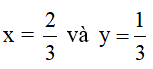 biểu thức A có giá trị là
biểu thức A có giá trị là 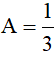
Câu 2. Thực hiện được đúng phép chia A= 2x4 + 3x3 - 4x2 -3x +2 và đa thức B = x + 2
1) (2x4 + 3x3 - 4x2 -3x +2) : (x+2) = 2x3-x2-2x + 1
2) 2x3-x2-2x + 1= 2x( x2-1)-(x2-1) = (x2 - 1)(2x-1) =(x-1)(x+1)(2x-1)
Câu 3
1) Chỉ ra được MC // ND
Do đó tứ giác MNDC là hình bình hành
2) Chỉ ra được NF // AE
và N là trung điểm cạnh AD của tan giác DAE
→ F là trung điểm của DE
3) Ta có: 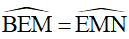 (cặp góc so le trong)
(cặp góc so le trong)
Chỉ ra được tam giác MED cân tại M 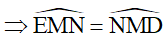
Chỉ ra được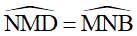
Do đó 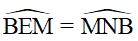
Mặt khác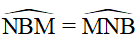 (tam giác BMN cân tại M)
(tam giác BMN cân tại M)
Và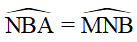 (cặp góc so le trong)
(cặp góc so le trong)
Vậy 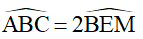
Câu 4.
Ta có: (x+y+z)3 = x3+y3+z3 + 3(x+y)(y+z)(z+x)
Kết hợp với các điều kiện đã cho, ta có:(x+y)(y+z)(z+x)= 0
→ Một trong các thừa số của tích(x+y)(y+z)(z+x) phải bằng 0
Giả sử (x + y) = 0, kết hợp với điều kiện: x + y + z = 1 → z = 1
Kết hợp với điều kiện: x2+y2+z2= 1→ x = y = 0
Vậy trong 3 số x, y, z phải có 2 số bằng 0 và 1 số bằng 1.
Vậy S = 1
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 8)
Bài 1. (2 điểm) Thực hiện phép tính:
a) 3x2( 2x2-5x -4)
b) (x+1)2 + (x-2)(x+3) -4x
Bài 2. (2,0 điểm) Phân tích đa thức thành nhân tử
a) 7x2 + 14xy
b)3( x+4) -x2- 4x
c) x2-2xy + y2 -z2
d) x2-2x -15
Bài 3. (2,0 điểm) Tìm x:
a) 7x2 + 2x
b) x( x+4)- x2- 6x =10
c) x( x-1) + 2x -2 =0
d) ( 3x-1)2 - ( x+5)2 = 0
Bài 4. (3,5 điểm)
Cho tam giác ABC có 3 góc nhọn và AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Trên tia đối của MH lấy điểm K sao cho HM = MK.
a) Chứng minh: Tứ giác BHCK là hình bình hành.
b) Chứng minh: BK ⊥ AB và CK ⊥ AC
c) Gọi I là điểm đối xứng với H qua BC. Chứng minh: Tứ giác BIKC là hình thang cân.
d) BK cắt HI tại G. Tam giác ABC phải có thêm điều kiện gì đề tứ giác GHCK là hình thang cân.
Bài 5. (0,5 điểm)
Chứng minh rằng: 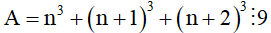 với mọi
với mọi 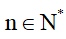
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 9)
I. TRẮC NGHIỆM
Câu 1 : Với giá trị nào của a thì biểu thức 16x2+ 24x + a viết được dưới dạng bình phương của một tổng ?
A. a = 1
B. a = 9
C. a = 16
D. a = 25
Câu 2 : Phân tích đa thức 4x2 - 9y2 + 4x – 6y thành nhân tử ta được :
A. (2x - 3y)(2x + 3y – 2)
B. (2x + 3y)(2x - 3y – 2)
C. (2x - 3y)(2x + 3y + 2)
D .(2x + 3y)(2x - 3y + 2)
Câu 3 : Cho hình thang ABCD (AB // CD), các tia phân giác của góc A và B cắt nhau tại điểm E trên cạnh CD . Ta có
A. AB = CD + BC
B . AB = DC + AD
C. DC = AD + BC
D. DC = AB – BC
Bài 2 : Các khẳng định sau đúng hay sai ?
a) Hai điểm đối xứng với nhau qua điểm O khi điểm O cách đều 2 đầu đoạn thẳng nối 2 điểm đó.
b) Tứ giác có 2 cạnh đối bằng nhau là hình bình hành
c) Đơn thức A thỏa mãn 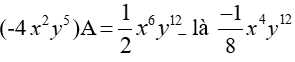
II. Tự luận (8,5 điểm)
Bài 1 : (1,5 điểm) . Cho biểu thức : A =(x-2)3 – x2(x – 4) + 8
B = ( x2– 6x + 9):(x – 3) – x(x + 7) – 9
a. Thu gọn biểu thức A và B với x≠3
b. Tính giá trị của biểu thức A tại x = -1
c. Biết C = A + B. Chứng minh C luôn âm với mọi giá trị của x ≠ 3
Bài 2 : (1,5 điểm) Phân tích các đa thức sau thành nhân tử:
a) x2(x – y) + 2x – 2y
b) (5x – 2y)(5x + 2y) + 4y - 1
c) x2(xy + 1) + 2y – x – 3xy
Bài 3 : (1,5 điểm) Tìm x biết:
a, x2(2x-3) - 2(3-2x) = 0
b. (x + 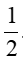 )2 - (x+
)2 - (x+ 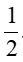 )(x+6) =8
)(x+6) =8
c. (x2+2x)2 - 2x2-4x =3
Bài 4 : (3,5 điểm) Cho tam giác ABC vuông cân tại A. Trên đoạn thẳng AB lấy điểm E, trên tia đối của tia CA lấy điểm F sao cho BE = CF . Vẽ hình bình hành BEFD. Gọi I là giao điểm của EF và BC. Qua E kẻ đường thẳng vuông góc với AB cắt BI tại K.
a)Chứng minh rằng : Tứ giác EKFC là hình bình hành
b) Qua I kẻ đường thẳng vuông góc với AF cắt BD tại M. CMR : AI = BM
c) CMR : C đối xứng với D qua MF
d) Tìm vị trí của E trên AB để A, I, D thẳng hàng.
Bài 5 :(0,5 điểm)Cho x, y, z là các số thực khác 0 thỏa mãn x + y + z = 3 và x2 + y2 + z2 = 9
Tính giá trị biểu thức P = 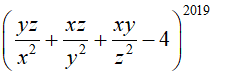
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 10)
Bài 1: Làm tính nhân:
a, 2x(2xy – 5x2 + 4)
b) ( 2x2+ 5x2y - 3xy)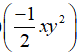
Bài 2 : (1,5đ) Tìm x,y biết:
a) x2 – 16x = 0
b) 9 x2+ 6x + 4y2 – 8y +5 = 0
Bài 3 :(2đ) Phân tích đa thức thành nhân tử :
a, x2-2xy + x- 2y
b) x2 -5x +6
c. x2 - y2 + 2x2 +2xy
d) x5 + x+ 1
Bài 4 : (1 đ) Cho A = 3x3 -2x2 + ax - a – 5 và B = x – 2. Tìm a để A⋮B
Bài 5 : ( 3,5đ)
Cho hình chữ nhật MNPQ. Gọi A là chân đường vuông góc hạ từ P đến NQ. Gọi B;C; D lần lượt là trung điểm của PA; AQ; MN.
a, Chứng minh rằng : BC//MN
b,Chứng minh rằng tứ giác CDNB là hình bình hành
c. Gọi E là giao điểm của NB và PC, gọi F là chân đường vuông góc hạ từ D đến NB. Chứng minh rằng tứ giác FDCE là hình chữ nhật
d,Hạ CG vuông góc với MN tại G; BC cắt NP tại H, chứng minh rằng DB cắt GH tại trung điểm mỗi đường.
Bài 6 : (0,5đ) Cho x,y là hai số thực thỏa mãn x2+ y2– 4x + 3 = 0 Tìm giá trị lớn nhất, nhỏ nhất của M = x2+ y2
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 11)
Bài 1: Thực hiện các phép tính:
a) -7x2(3x - 4y)
b) (x - 3)(5x - 4)
c) (2x - 1)2
d) (x + 3)(x - 3)
Bài 2: Phân tích đa thức thành nhân tử:
a) 2x3 - 3x2
b) x2 + 5xy + x + 5y
c) x2 - 36 + 4xy + 4y2
Bài 3: Tìm, biết: x2 - 5x + 6 = 0
Bài 4: Có 10 túi đựng tiền vàng hình dạng giống hệt nhau. Trong đó, có một túi đựng tiền giả. Những đồng tiền giả nhẹ hơn một gam so với đồng tiền thật nặng 10 gam. Bằng một chiếc cân đồng hồ và với chỉ một lần cân, hãy tìm ra túi đựng tiền giả?
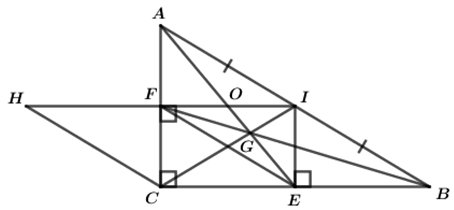
Bài 5: Cho ΔABC vuông tại C (AC < BC), gọi I là trung điểm của AB. Kẻ IE ⊥ BC tại E, kẻ IF ⊥ BC tại F.
a. Chứng minh tứ giác CEIF là hình chữ nhật.
b. Gọi H là điểm đối xứng của I qua F. Chứng minh rằng tứ giác CHFE là hình bình hành.
CI cắt BF tại G, O là trung điểm của FI. Chứng minh ba điểm A, O, G thẳng hàng.
Bài 6:
Tìm các số a,b,c ∈ Q biết a2 + b2 + c2 = ab + bc + ac và a + b + c = 2019.
Đáp án đề thi giữa kì 1 môn Toán 8 - Đề số 11
Bài 1:
a)
-7x2(3x - 4y)
= -7x2.3x + 7x2.4y
= -21x3 + 28x2y
b)
(x - 3)(5x - 4)
= x.5x - x.4 - 3.5x + 3.4
= 5x2 - 4x - 15x + 12
= 5x2 - 19x + 12
c)
(2x - 1)2 = 4x2 - 4x + 1
d)
(x + 3)(x - 3) = x2 - 32 = x2 - 9
Bài 2:
a) 2x3 - 3x2 = x2(2x - 3)
b)
x2 + 5xy + x + 5y
= x(x + 5y) + (x + 5y)
= (x + 1)(x + 5y)
c)
x2 - 36 + 4xy + 4y2
= (x2 + 4xy + 4y2) - 36
= (x + 2y)2 - 62
= (x + 2y - 6)(x + 2y + 6)
Bài 3:
x2 - 5x + 6 = 0
x2 - 2x - 3x + 6 = 0
(x2 - 2x) - (3x - 6) = 0
(x - 3)(x - 2 = 0)
Trường hợp 1: x - 3 = 0 ⇒ x = 3
Trường hợp 2: x - 2 = 0 ⇒ x = 2
Vậy x ∈ {2, 3}
Bài 4:
Đánh số 10 ví theo thứ tự 1, 2, 3, ..., 10.
Lấy từ ví 1 - 1 đồng
Lấy từ ví 2 - 2 đồng
...
Lấy từ ví 10 - 10 đồng
⇒ Ta lấy được tất cả 55 đồng.
Khi đó, 55 đồng này sẽ cân nặng a gam (a > 0)
Giả sử 55 đồng này đều là tiền thật thì chúng có cân nặng là: 10.55 = 550(gam)
Mà tiền giả nhẹ hơn một gam so với tiền thật nên a < 550
Sau khi cân, thực hiện phép tính 550 - a
Nếu 550 - a = 9 thì ví 1 là ví đựng tiền giả.
Nếu 550 - a = 9.2 thì ví 2 là ví đựng tiền giả.
...
Bài 5:
a.
Vì ΔABC vuông tại C nên ∠C = 90o
Ta lại có: IE ⊥ BC tại E và IF ⊥ AC tại F.
⇒ ∠E = 90o, ∠F = 90o
Xét tứ giác IFCE ta có: ∠C = ∠E = ∠F = 90o
⇒ Tứ giác IFCE là hình chữ nhật (dấu hiệu nhận biết).
b.
Vì tứ giác IFCE là hình chữ nhật nên IF = CE và IF // CE.
Vì H là điểm đối xứng của I qua F nên IF = HF và H, F, I thẳng hàng.
⇒ CE = HF và CE // HF
⇒ Tứ giác CHFE là hình bình hàng (dấu hiệu nhận biết hình bình hành)
c.
*) Chứng minh A, G, E thẳng hàng
Giả sử BF ∩ CI = {G}
Xét tam giác ABC ta có:
IA = IB
IF // BC
⇒ F là trung điểm AC.
Tương tự, E là trung điểm của BC
⇒ BF là đường trung tuyến của ΔABC; AE là là đường trung tuyến của ΔABC
Mà CI là là đường trung tuyến của ΔABC và BF ∩ CI = {G}
⇒ G là trọng tâm của ΔABC
⇒ A, G, E thẳng hàng (1)
*) Chứng minh A, O, E thẳng hàng
Ta có:
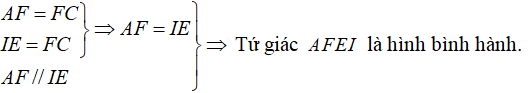
Mà O là trung điểm của IF nên O là trung điểm của AE.
⇒ A, O, E thẳng hàng (2)
Từ (1) và (2) suy ra A, O, G thẳng hàng.
Bài 6:
Theo giả thiết, ta có:
a2 + b2 + c2 = ab + bc + ac
2(a2 + b2 + c2) = 2(ab + bc + ac)
2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ac
2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac = 0
a2 -2ab + b2 + a2 - 2ac + c2 + b2 - 2bc + c2 = 0
(a - b)2 + (a - c)2 + (b - c)2 = 0
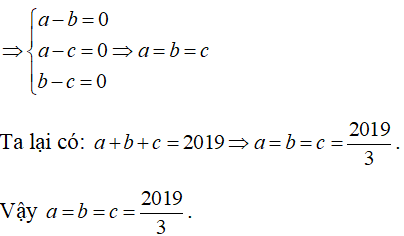
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 12)
PHẦN I: TRẮC NGHIỆM
Câu 1: Kết quả phép tính x(x - y) + y(x + y) tại x = -3 và y = 4 là:
A. 1
B. 7
C. -25
Câu 2: Khai triển biểu thức (x - 2y)3 ta được kết quả là:
A. x3 - 8y3
B. x3 - 2y3
C. x3 - 6x2y + 6xy2 - 2y3
D. x3 - 6x2y + 12xy2 - 8y3
Câu 3: Giá trị biểu thức 20092 - 2018.2009 + 10092 có bao nhiêu chữ số 0 ?
A. 6
B. 2
C. 4
Câu 4: Đa thức 4x2 - 12x + 9 phân tích thành nhân tử là:
A. (2x - 3)2
B. 2x + 3
C. 4x - 9
Câu 5: Hình nào sau đây là tứ giác có hai đường chéo bằng nhau?
A. Hình thang
B. Hình thang cân
C. Hình thang vuông
D. Hình bình hành
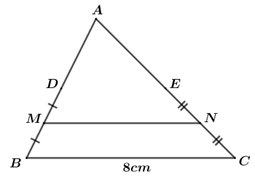
Câu 6: Cho tam giác ABC có cạnh BC = 8cm và D, E, M, N lần lượt là trung điểm của AB, AC, BD và CE (như hình vẽ). Khi đó, độ dài của MN là
A. 7cm
B. 5cm
C. 6cm
D. 4cm
Câu 7: Cho hình bình hành ABCD có ∠A = 60o. Khi đó, hệ thức nào sau đây là không đúng?

Câu 8: Hình chữ nhật có độ dài cạnh 5cm và 12cm thì khoảng cách từ giao điểm hai đường chéo đến mỗi đỉnh là
A. 17cm
B. 8,5cm
C. 6,5cm
D. 13cm
PHẦN II: TỰ LUẬN (8 điểm)
Câu 1 (VD) (2,25 điểm)
Rút gọn các biểu thức sau:
a. 2x(3x + 2) - 3x(2x + 3)
b. (x + 2)3 + (x - 3)2 - x2(x + 5)
c. (3x3 - 4x2 + 6x) : 3x
Câu 2 (VD) (0,75 điểm)
Phân tích đa thức sau thành nhân tử: 2x3 - 12x2 + 18x
Câu 3 (VD) (1,0 điểm)
Tìm x, biết: 3x(x - 5) - x2 + 25 = 0
Câu 4 (VD) (3,0 điểm) Cho hình bình hành ABCD (AB > AD). Gọi E và K lần lượt là trung điểm của CD và AB. BD cắt AE, AC, CK lần lượt tại N, O và I. Chứng minh rằng:
a. Tứ giắc AECK là hình bình hành.
b. Ba điểm E, O, K thẳng hàng.
c. DN = NI = IB
d. AE = 3KI
Câu 5 (VDC) (1,0 điểm) Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:
P = x2 + 5y2 + 4xy + 6x + 16y + 32
Đáp án đề thi giũa kì 1 môn Toán 8 - Đề số 12
A. PHẦN TRẮC NGHIỆM
Câu 1:
Thay x = -3 và y = -4 vào biểu thức x(x - y) + y(x + y) ta được:
(-3)(-3 - 4) + 4(-3 + 4) = 21 + 4 = 25
Chọn D.
Câu 2:
Ta có:
(x - 2y3 = x3 - 3x2.2y + 3x.(2y)2 + (2y)3 = x3 - 6x2y + 12xy2 - 8y3
Chọn D.
Câu 3:
20092 - 2018.2009 + 10092
20092 - 2.2009.1009 + 10092
= (2009 - 1009)2
= 10002
= 1000000
Vậy giá trị của biểu thức 20092 - 2018.2009 + 10092 có 6 chữ số 0.
Chọn A.
Câu 4:
4x2 - 12x + 9 = (2x)2 - 2.2x.3 + 32 = (2x - 3)2
Chọn A.
Câu 5:
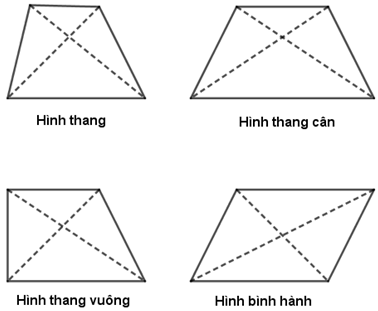
Quan sát hình vẽ, và áp dụng tính chất của các hình ta có: Hình thang cân là hình có hai đường chéo bằng nhau.
Chọn B.
Câu 6:

Chọn D.
Câu 7:
Vì ABCD là hình bình hành nên ta có: ∠A = ∠C, ∠B = ∠D và AB // CD, AD // BC
Mà ∠A = 60o ⇒ ∠C = 60o
⇒ Đáp án C đúng.
Vì AD // BC mà ∠A và ∠B ở vị trí trong cùng phía nên ta có: ∠A + ∠B = 180o ⇒ ∠B = 120o
⇒ ∠B = 2∠C ⇒ Đáp án B đúng.
⇒ ∠A = ∠B/2 ⇒ Đáp án D đúng.
Vì AB // CD mà ∠A và ∠D ở vị trí trong cùng phía nên ta có: ∠A + ∠D = 180o ⇒ ∠D = 120o
⇒ Đáp án A sai.
Chọn A.
Câu 8:
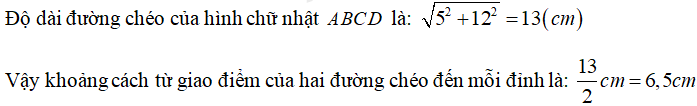
Chọn C.
PHẦN II: TỰ LUẬN
Bài 1.
a.
2x(3x + 2) - 3x(2x + 3)
= 2x.3x + 2x.2 - 3x.2x - 3x.3
= 6x2 + 4x - 6x2 - 9x
= -5x
b.
(x + 2)3 + (x - 3)3 - x2(x + 5)
= (x3 + 6x2 + 12x + 8) + (x2 - 6x + 9) - (x3 + 5x2)
= x3 + 6x2 + 12x + 8 + x2 - 6x + 9 - x3 - 5x2
= (x3 - x3) + (6x2 + x2 - 5x2) + (12x - 6x) + 9
= 2x2 + 6x + 9
c.
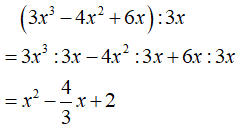
Bài 2.
2x3 - 12x2 + 18x
= 2x(x2 - 6x + 9)
= 2x(x - 3)2
Bài 3.
3x(x - 5) - x2 + 25 = 0
3x(x - 5) - (x2 + 25) = 0
3x(x - 5) - (x + 5)(x - 5) = 0
(3x - x - 5)(x - 5) = 0
(2x - 5)(x - 5) = 0
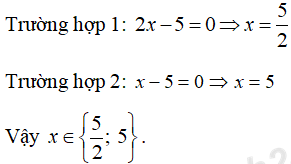
Bài 4.
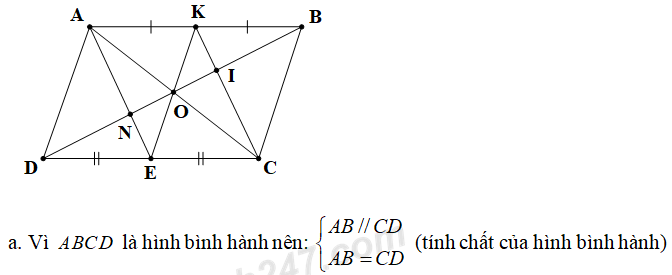
Mà E, K lần lượt là trung điểm của CD và AB nên AK = EC VÀ AK // EC.
⇒ Tứ giác AECK là hình bình hành (dấu hiệu nhận biết)
b. Trong hình bình hành ABCD có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD (tính chất của hình bình hành)
Mà AECK là hình bình hành nên O là trung điểm của EK.
⇒ Ba điểm E, O, K thẳng hàng.

Bài 5.
P = x2 + 5y2 + 4xy + 6x + 16y + 32
⇒ P = x2 + (4xy + 6x) + 5y2 + 16y + 32
⇒ P = x2 + 2x(2y + 3) + (2y + 3)2 - (2y + 3)2 + 5y2 + 16y + 32
⇒ P = [x + (2y + 3)]2 - 4y2 - 12y - 9 + 5y2 + 16y + 32
⇒ P = (x + 2y + 3)2 + y2 + 4y + 23
⇒ P = (x + 2y + 3)2 + (y + 2)2 + 19
Vì (x + 2y + 3)2 ≥ 0 với mọi x, y ∈ R
(y + 2)2 ≥ 0 với mọi y ∈ R
⇒ P = (x + 2y + 3)2 + (y + 2)2 + 19 ≥ 19 với mọi x, y ∈ R
Dấu "=" xảy ra khi và chỉ khi x + 2y + 3 = 0 và y + 2 =0
Suy ra, x = 1 và y = -2
Vậy P đạt giá trị nhỏ nhất bằng 19 tại x = 1 và y = -2.
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 13)
Bài 1 (4,5 điểm). Phân tích các đa thức sau thành nhân tử:
a) 4x2 + 4x3 -x2 -x
b) 1 - 2a + 2bc + a2 -b2 - c2
c) ( x - 7)( x - 5)(x - 4)(x - 2) - 72
Bài 2 (1,5 điểm). Tìm x sao cho:
(x + 5)(4 - 3x)- (3x+ 2)2 + (2x + 1)3 = (2x - 1)(4x2 + 2x + 1)
Bài 3 (3 điểm). Cho có M và N lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia MN lấy điểm D sao cho NM = ND. Gọi I là trung điểm của đoạn thẳng AM.
a) Tứ giác ADCM là hình gì? vì sao?
b) Chứng minh rằng: B, I, D thẳng hàng.
c) Qua điểm D kẻ đường thẳng song song với AC, cắt đường thẳng BC tại E. Đường thẳng IN cắt DE tại F. Tìm điều kiện của để tứ giác MNFE là hình thang cân.
Bài 4 (1 điểm).
a) Tìm giá trị nhỏ nhất của biểu thức A = 2x2 - x + 2017
b) (Dành riêng cho lớp 8A)
Cho ba số nguyên a, b, c có tổng chia hết cho 6
Chứng minh rằng biểu thức M= (a+b)(b+c)(c+a) - 2abc chia hết cho 6
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 14)
PHẦN I. TRẮC NGHIỆM
Câu 1. Kết quả rút gọn biểu thức: (3x + 2)(3x - 2) là:
A) 3x2 + 4
B) 3x2 - 4
C) 9x2 + 4
D) 9x2 -4
Câu 2. Đơn thức 12x2y3z chia hết cho đơn thức nào sau đây?
A) 3x3yz
B) 4xy2z2
C) -5xy2
D) 3xyz2
Câu 3. Khẳng định nào sau đây là đúng?
A. Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.
B. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
C. Hình thang có một góc vuông là hình chữ nhật
D. Hình thang cân có hai đường chéo bằng nhau là hình chữ nhật.
Câu 4. Hình nào dưới đây luôn có tâm đối xứng?
A. Hình thang
B. Hình thang cân
C. Hình bình hành
D. Cả A, B, C
PHẦN II. TỰ LUẬN
Bài 1. Phân tích các đa thức sau thành nhân tử.
a) 2xy + 3z + 6y +xz
b) 16x2 -(x +1)2
c) x2 - 6x -7
d) x3 - 2x2 + 2x -1
Bài 2.Tìm x, biết:
a) x(x - 2) - x + 2= 0
b) x2 - 25 - (x + 5) = 0
c) (10x + 9)x - (5x - 1)(2x + 3)=0
Bài 3
a) Rút gọn rồi tính giá trị của biểu thức sau:
(x - y)(x2 + xy + y2 ) + 2y3 tại 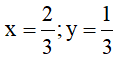
b) Làm tính chia: ( 30x4y3 - 20x2y3 + 6x4y4) : 5x2y3
Bài 4 . Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OB, OD.
a) Tứ giác AECF là hình gì? Vì sao?
b) Gọi H là giao điểm của AF và DC, K là giao điểm của CE và AB. Chứng minh AH = CK
c) Qua O kẻ đường thẳng song song với CK cắt DC tại I.
Chứng minh rằng: DI = 2CI
Bài 5 . Ông Văn có 24m hàng rào rất đẹp, ông muốn rào một sân vườn hình chữ nhật để đạt được diện tích lớn nhất. Vườn ngay sát tường nhà để một chiều không phải rào. Hỏi kích thước sân vườn đó là bao nhiêu?
__________________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 1
Năm học 2022 - 2023
Môn: Toán 8
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán lớp 8 có đáp án - (Đề số 15)
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Câu 1: Kết quả của phép tính (x+2y)(y+2x)= ?
A. 2x2 +5xy +2y2
B. 2x3 +2y2
C. x2 +4xy +4y2
D. 2x2 +4xy +2y2
Câu 2: Kết quả của phép chia (2x3 + x2 -2x +1): (x2 +1)
A. 2x+1
B.-2x-1
C. 1-2x
D. 2x - 1
Câu 3: Giá trị của biểu thức: x2-4x +4 tại x=-1 là:
A. -1
B. 1
C. -9
D. 9
Câu 4: Biết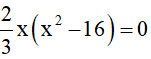 . Các số x tìm được là:
. Các số x tìm được là:
A. 0; 4; -4
B. 0; 16; -16
C. 0; 4
D. 4; -4
Câu 5: Hình thang ABCD (AB // CD), M là trung điểm AD, N là trung điểm BC. Biết:
CD= 8cm; MN=6cm. Độ dài đoạn AB là:
A. 2cm
B.4cm
C.6cm
D. 8cm
Câu 6. Tứ giác ABCD là hình bình hành nếu có:
A. ∠A = ∠C
B. AB // CD
C. AB = CD; AD = BC
D. BC = AD
II. TỰ LUẬN (7 điểm)
Câu 1: (1,5điểm) Cho biểu thức sau:
A= (x-1)(x+1) + (x-2)(x2 +2x +4) -x(x2 +x-2)
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức A tại 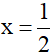 .
.
Câu 2: (1,5 điểm) Phân tích đa thức thành
a) x2 – 2xy + x – 2y
b) x3 – y3 + 2x2 + 2xy
c) x5 + x + 1
Câu 3: (3,5 điểm) Cho hình chữ nhật MNPQ. Gọi A là chân đường vuông góc hạ từ P đến NQ. Gọi B; C; D lần lượt là trung điểm của PA; AQ; MN.
a) Chứng minh rằng: BC//MN
b) Chứng minh rằng tứ giác CDNB là hình bình hành
c) Gọi E là giao điểm của NB và PC, gọi F là chân đường vuông góc hạ từ D đến NB. Chứng minh rằng tứ giác FDCE là hình chữ nhật
d) Hạ CG vuông góc với MN tại G; BC cắt NP tại H, chứng minh rằng DB cắt GH tại trung điểm mỗi đường.
Câu 4: (0,5 điểm)
Cho x,y là hai số thực thỏa mãn: x2 + y2 – 4x + 3 = 0
Tìm giá trị lớn nhất, nhỏ nhất của M = x2 + y2