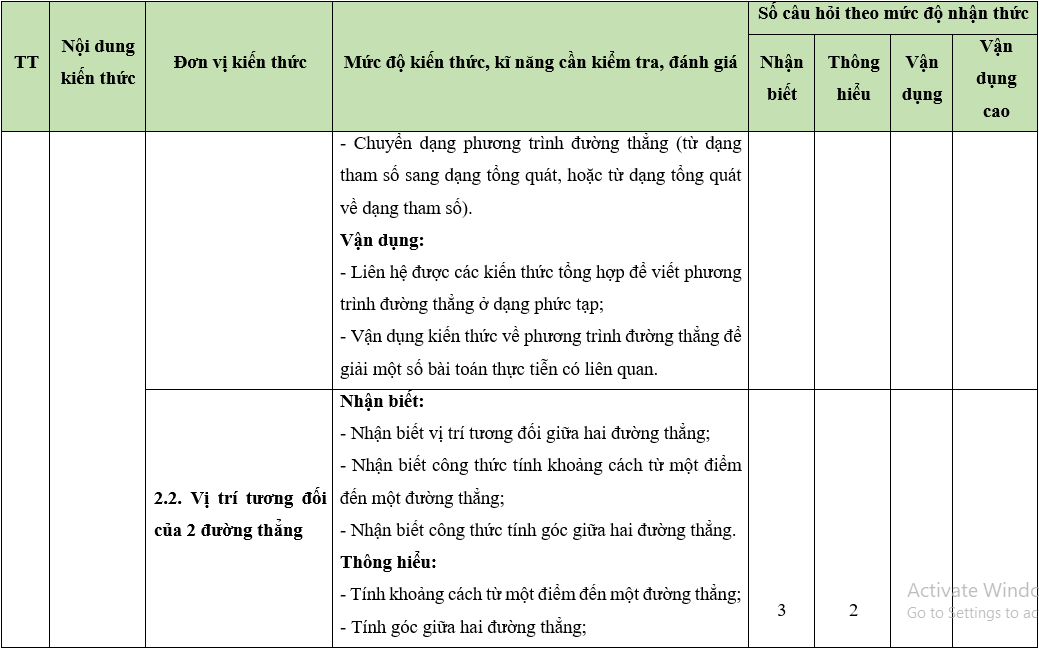
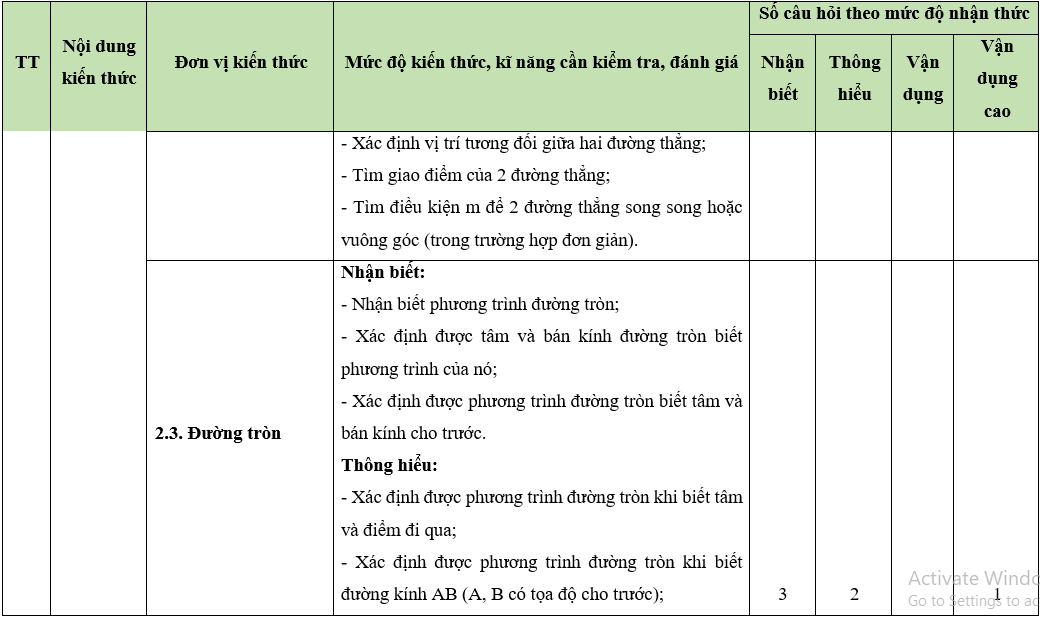
Bộ 30 đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức có đáp án
Bộ 30 đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức có đáp án giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 10 Giữa học kì 2. Mời các bạn cùng đón xem:
[Năm 2023] Đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức có đáp án
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 10
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức có đáp án - (Đề số 1)
I. Trắc nghiệm (7 điểm)
Câu 1. Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?
A. 2x + y = 5;
B. + y = 5;
C. ;
D. 2x2 – 3y2 = 0.
Câu 2. Cho hàm số dưới dạng bảng như sau:
|
x |
0 |
1 |
2 |
3 |
4 |
|
y |
0 |
1 |
4 |
9 |
16 |
Giá trị của hàm số y tại x = 1 là
A. 1;
B. 4;
C. 9;
D. 16.
Câu 3. Cho hàm số y = f(x) có đồ thị như hình dưới.
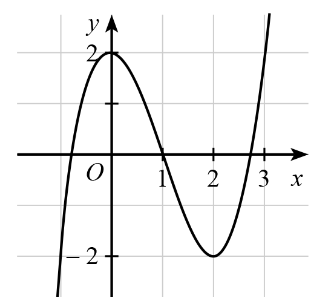
Hàm số trên nghịch biến trên khoảng
A. (– ∞; 2);
B. (2; + ∞);
C. (0; 2);
D. (– ∞; 0).
Câu 4. Hàm số có tập xác định là
A. (– 2; 5);
B. [– 2; 5];
C. (– ∞; – 2] ∪ [5; + ∞);
D. ℝ \ {– 2; 5}.
Câu 5. Cho hàm số . Giá trị của hàm số tại x = 5 là
A. – 1998;
B. 0;
C. 1;
D. Không tồn tại.
Câu 6. Trong các hàm số sau, hàm số nào không phải là hàm số bậc hai?
A. y = x2 – 2x + 1;
B. y = (x2)2 – 3x2 + 6;
C. y = x2 + 5x + 9;
D. y = 10 – 4x – x2.
Câu 7. Cho đồ thị hàm số bậc hai y = ax2 + bx + c (a ≠ 0) như hình vẽ sau.
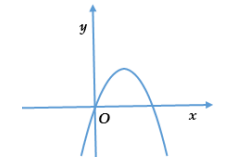
Điều kiện của hệ số a của hàm số bậc hai này là
A. a = 1;
B. a > 1;
C. a > 0;
D. a < 0.
Câu 8. Đồ thị của hàm số bậc hai y = – x2 + 5 + 3x có trục đối xứng là
A. ;
B. ;
C. x = 3;
D. x = 5.
Câu 9. Cho hàm số bậc hai f(x) = – 2x2 – x + 1. Giá trị lớn nhất của hàm số là
A. ;
B. ;
C. ;
D. Không tồn tại.
Câu 10. Cho hàm số bậc hai có bảng biến thiên như sau:
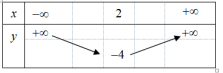 Công thức hàm số bậc hai trên là
Công thức hàm số bậc hai trên là
A. y = – x2 + 4x;
B. y = x2 + 4x;
C. y = x2 – 4x;
D. y = – x2 – 4x.
Câu 11. Biểu thức nào dưới đây không phải là tam thức bậc hai?
A. f(x) = 2x2 + 5x – 3;
B. f(x) = x2 – 9;
C. f(x) = 32x2 + 3x + 4;
D. f(x) = x4 – 2x2 + 5.
Câu 12. Cho tam thức bậc hai f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Mệnh đề nào sau đây đúng?
A. Nếu ∆ > 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ;
B. Nếu ∆ < 0 thì f(x) luôn trái dấu với hệ số a, với mọi x ∈ ℝ;
C. Nếu ∆ = 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ \ ;
D. Nếu ∆ < 0 thì f(x) luôn cùng dấu với hệ số b, với mọi x ∈ ℝ.
Câu 13. Cho hàm số y = f(x) có đồ thị như hình dưới đây.
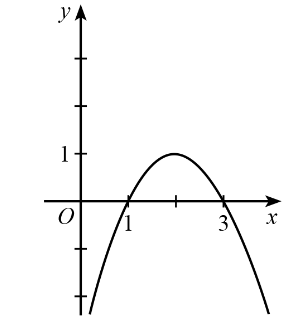 Trong các phát biểu sau, phát biểu nào sai?
Trong các phát biểu sau, phát biểu nào sai?
A. f(x) < 0 khi và chỉ khi x ∈ (1; 3);
B. f(x) ≤ 0 khi và chỉ khi x ∈ (– ∞; 1] ∪ [3; + ∞);
C. f(x) > 0 khi và chỉ khi x ∈ (1; 3);
D. f(x) ≥ 0 khi và chỉ khi x ∈ [1; 3].
Câu 14. Tam thức nào sau đây luôn dương với mọi giá trị của x?
A. x2 – 10x + 2;
B. x2 – 2x – 10;
C. x2 – 2x + 10;
D. – x2 + 2x + 10.
Câu 15. Gọi S là tập nghiệm của bất phương trình x2 – 8x + 7 ≥ 0. Tromg các tập hợp sau, tập nào không là tập con của S?
A. (– ∞; 0];
B. [6; + ∞);
C. [8; + ∞];
D. (– ∞; – 1].
Câu 16. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình là tập nghiệm của phương trình ax2 + bx + c = (dx + e)2;
B. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình dx + e ≥ 0;
C. Mọi nghiệm của phương trình ax2 + bx + c = (dx + e)2 đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình ax2 + bx + c ≥ 0.
Câu 17. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình là tập nghiệm của phương trình ax2 + bx + c = dx2 + ex + f;
B. Tập nghiệm của phương trình là tập nghiệm của phương trình (ax2 + bx + c)2 = (dx2 + ex + f)2;
C. Mọi nghiệm của phương trình ax2 + bx + c = dx2 + ex + f đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = dx2 + ex + f thỏa mãn bất phương trình ax2 + bx + c ≥ 0 (hoặc dx2 + ex + f ≥ 0).
Câu 18. Phương trình có số nghiệm là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 19. Cho phương trình (1). Để phương trình (1) có nghiệm thì m ∈ [a; b]. Giá trị a2 + b2 bằng
A. 2;
B. 4;
C. 1;
D. 3.
Câu 20. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng d là
A. ;
B. ;
C. ;
D. .
Câu 21. Điểm nào dưới đây không thuộc đường thẳng d: 2x – 5y + 3 = 0?
A. A (1; 1);
B. B ;
C. C ;
D. D (2; 3).
Câu 22. Phương trình tham số của đường thẳng ∆ đi qua điểm A(– 4; 2) và nhận làm vectơ chỉ phương là
A. ;
B. ;
C. ;
D. .
Câu 23. Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận làm vectơ pháp tuyến là
A. 2x – 7y + 23 = 0;
B. – 2x + 7y – 23 = 0;
C. 2x – 7y – 23 = 0;
D. – 2x – 7y + 23 = 0.
Câu 24. Cho đường thẳng d có phương trình tổng quát: x + 2y – 3 = 0. Phương trình tham số của đường thẳng d là
A. ;
B. ;
C. ;
D. .
Câu 25. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
A. ;
B. ;
C. ;
D. .
Câu 26. Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: (*).
Khi đó, ∆1 trùng với ∆2 khi và chỉ khi
A. hệ (*) có vô số nghiệm;
B. hệ (*) vô nghiệm;
C. hệ (*) có nghiệm duy nhất;
D. hệ (*) có hai nghiệm.
Câu 27. Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0. Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức
A. ;
B. ;
C. ;
D. .
Câu 28. Trong mặt phẳng tọa độ, cho hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0,
với các vectơ pháp tuyến và tương ứng. Khi đó góc φ giữa hai đường thẳng đó được xác định bởi công thức
A. ;
B. ;
C. ;
D. .
Câu 29. Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
A. ;
B. ;
C. 26;
D. .
Câu 30. Góc giữa hai đường thẳng a: 6x – 5y + 15 = 0 và b: bằng
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Câu 31. Phương trình nào sau đây là phương trình đường tròn?
A. x2 + 2y2 – 4x – 8y + 1 = 0;
B. x2 + y2 – 4x + 6y – 12 = 0;
C. x2 + y2 – 2x – 8y + 20 = 0;
D. 4x2 + y2 – 10x – 6y – 2 = 0.
Câu 32. Đường tròn (x + 3)2 + (y – 4)2 = 16 có tâm là
A. I(3; 4);
B. I(3; – 4);
C. I(– 3; 4);
D. I(– 3; – 4).
Câu 33. Phương trình nào sau đây là phương trình của đường tròn tâm I(1; 2), bán kính bằng 5?
A. x2 + y2 – 2x – 4y – 20 = 0;
B. x2 + y2 + 2x + 4 + 20 = 0;
C. x2 + y2 + 2x + 4y – 20 = 0;
D. x2 + y2 – 2x – 4y + 20 = 0.
Câu 34. Phương trình đường tròn đường kính AB với A(1; 3) và B(5; – 1) là
A. (x + 3)2 + (y – 1)2 = 8;
B. (x + 3)2 + (y + 1)2 = 8;
C. (x – 3)2 + (y + 1)2 = 8;
D. (x – 3)2 + (y – 1)2 = 8.
Câu 35. Trong mặt phẳng tọa độ, cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0 và điểm A(1; 5). Tiếp tuyến của đường tròn (C) tại điểm A có phương trình là
A. y – 5 = 0;
B. y + 5 = 0;
C. x + y – 5 = 0;
D. x – y – 5 = 0.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Giải các phương trình sau:
a) ;
b) .
Bài 2. (1 điểm) Viết phương trình tổng quát của đường thẳng
a) đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
b) đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.
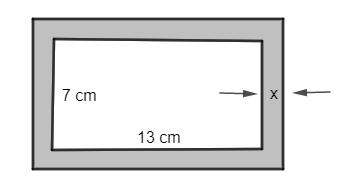
Bài 3. (1 điểm) Hà dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 7 cm × 13 cm, độ rộng viền xung quanh là x cm (như hình vẽ). Diện tích của viền khung ảnh không vượt quá 44 cm2. Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu xen-ti-mét?
Đáp án đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức - Đề số 1
I. Bảng đáp án trắc nghiệm
|
1. D |
2. A |
3. C |
4. B |
5. C |
6. B |
7. D |
|
8. A |
9. C |
10. C |
11. D |
12. C |
13. A |
14. C |
|
15. B |
16. B |
17. D |
18. B |
19. C |
20. B |
21. D |
|
22. B |
23. C |
24. A |
25. B |
26. A |
27. A |
28. C |
|
29. A |
30. B |
31. B |
32. C |
33. A |
34. D |
35. A |
II. Hướng dẫn giải một số câu trắc nghiệm
Câu 3.
Đáp án đúng là: C
Từ hình vẽ ta thấy đồ thị hàm số y = f(x) đi xuống từ trái sang phải trên khoảng (0; 2). Vậy hàm số này nghịch biến trên khoảng (0; 2).
Câu 4.
Đáp án đúng là: B
Biểu thức có nghĩa khi
Vậy tập xác định của hàm số là D = [– 2; 5].
Câu 5.
Đáp án đúng là: C
Vì x = 5 > 0 nên y (5) = 1.
Câu 9.
Đáp án đúng là: C
Vì hệ số a = – 2 > 0 nên hàm số f(x) đạt giá trị lớn nhất tại đỉnh.
Do đó, giá trị lớn nhất của hàm số chính là tung độ đỉnh của đồ thị hàm số và là
.
Câu 10.
Đáp án đúng là: C
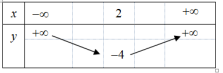
Từ bảng biến thiên suy ra hệ số a > 0, loại đáp án A và D.
Tọa độ đỉnh của đồ thị hàm số bậc hai là I(2; – 4), thay vào từng đáp án B và C, ta thấy đáp án C thỏa mãn.
Vậy công thức hàm số bậc hai có bảng biến thiên như hình vẽ là y = x2 – 4x.
Câu 15.
Đáp án đúng là: B
Ta có: x2 – 8x + 7 ≥ 0 ⇔ .
Suy ra tập nghiệm của bất phương trình là S = (– ∞; 1] ∪ [7; + ∞].
Do đó, [6; + ∞) ⊄ S.
Câu 18.
Đáp án đúng là: B
Bình phương hai vế của phương trình ta được
– x2 + 4x = 4x2 – 8x + 4.
Sau khi thu gọn ta được 5x2 – 12x + 4 = 0. Từ đó tìm được x = 2 hoặc .
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 19.
Đáp án đúng là: C
Ta có:
Để phương trình (1) có nghiệm thì 1 ≤ 2m + 3 ≤ 3 ⇔ – 1 ≤ m ≤ 0 ⇒ m ∈ [– 1; 0].
Suy ra a = – 1, b = 0, do đó a2 + b2 = 1.
Câu 24.
Đáp án đúng là: A
Đường thẳng d: x + 2y – 3 = 0 có một vectơ pháp tuyến là , do đó nó có một vectơ chỉ phương là , suy ra loại đáp án B và D.
Ở đáp án C, ta thấy khi t = 0 thì x = 2 và y = 1, thay vào phương trình d ta thấy không thỏa mãn nên loại đáp án C, vậy chọn đáp án A.
Câu 25.
Đáp án đúng là: B
Cách 1. Thay tọa độ các điểm A, B lần lượt vào các phương trình trong các đáp án thì thấy đáp án B không thỏa mãn.
Cách 2. Nhận thấy rằng các phương trình ở các đáp án A, C, D thì vectơ chỉ phương của các đường thẳng đó cùng phương, riêng chủ có đáp án B thì không. Do đó chọn đáp án B.
Câu 29.
Đáp án đúng là: A
Khoảng cách từ điểm M(5; – 1) đến d: 3x + 2y + 13 = 0 là
.
Câu 30.
Đáp án đúng là: B
Đường thẳng a có một vectơ pháp tuyến là ;
Đường thẳng b có một vectơ chỉ phương là nên nó có một vectơ pháp tuyến là .
Ta thấy: .
Suy ra góc giữa hai đường thẳng bằng 90°.
Câu 34.
Đáp án đúng là: D
Đường tròn đường kính AB có tâm là trung điểm I của AB và có bán kính bằng nửa độ dài đoạn AB.
Ta có , suy ra .
Suy ra bán kính đường tròn là .
Tọa độ tâm là . Suy ra I(3; 1).
Phương trình đường tròn cần lập là: (x – 3)2 + (y – 1)2 = 8.
Câu 35.
Đáp án đúng là: A
Ta có: 12 + 52 – 2 . 1 – 4 . 5 – 4 = 0, do đó A thuộc đường tròn (C).
Đường tròn (C) có tâm là I(1; 2). Tiếp tuyến của (C) tại A(1; 5) có vectơ pháp tuyến , nên có phương trình
0(x – 1) – 3(y – 5) = 0 hay y – 5 = 0.
III. Hướng dẫn giải tự luận
Bài 1. (1 điểm)
a) Bình phương hai vế của phương trình ta được:
3x2 – 4x + 5 = 2x2 – 3x + 11.
Sau khi thu gọn ta được x2 – x – 6 = 0. Từ đó tìm được x = 3 hoặc x = – 2.
Thay lần lượt các giá trị của x vừa tìm được vào phương trình đã cho ta thấy cả hai giá trị này đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S = {– 2; 3}.
b) Bình phương hai vế của phương trình ta được:
2x2 – 13x + 21 = x2 – 6x + 9.
Sau khi thu gọn ta được x2 – 7x + 12 = 0. Từ đó tìm được x = 4 hoặc x = 3.
Thay lần lượt các giá trị của x vừa tìm được vào phương trình đã cho ta thấy cả hai giá trị này đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S = {3; 4}.
Bài 2. (1 điểm)
a) Gọi đường thẳng cần lập là d.
Vectơ pháp tuyến của đường thẳng 3x + 5y – 2 = 0 cũng là một vectơ pháp tuyến của đường thẳng d nên phương trình đường thẳng d có dạng 3x + 5y + c = 0 (c ≠ – 2).
Vì d đi qua điểm M(– 1; – 4) nên 3 . (– 1) + 5 . (– 4) + c = 0. Suy ra c = 23 (t/m).
Vậy phương trình tổng quát của đường thẳng d là 3x + 5y + 23 = 0.
b) Gọi đường thẳng cần lập là a.
Đường thẳng a vuông góc với đường thẳng 2x + 3y + 7 nên lấy vectơ pháp tuyến của đường thẳng 2x + 3y + 7 là vectơ chỉ phương của đường thẳng a. Khi đó, một vectơ pháp tuyến của đường thẳng a là .
Đường thẳng a đi qua điểm N(1; 1) và có vectơ pháp tuyến là nên có phương trình là 3(x – 1) – 2(y – 1) = 0 hay 3x – 2y – 1 = 0.
Bài 3. (1 điểm)
Diện tích hình chữ nhật bên trong khung ảnh (không bao gồm viền) là 7 . 13 = 91 (cm2).
Vì độ rộng viền xung quanh là x cm nên x > 0 và kích thước của khung ảnh là (7 + 2x) cm × (13 + 2x) cm.
Diện tích viền khung ảnh là: (7 + 2x)(13 + 2x) – 91 = 4x2 + 40x (cm2).
Theo bài ra ta có: 4x2 + 40x ≤ 44.
Giải bất phương trình trên ta được x ∈ [– 11; 1]. Do x > 0 nên x ∈ (0; 1].
Vậy độ rộng viền khung ảnh lớn nhất là 1 cm.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 10
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức có đáp án - (Đề số 2)
I. Trắc nghiệm (7 điểm)
Câu 1. Trong các công thức sau, công thức nào biểu diễn y là hàm số của x?
A. x2 + 2y2 = 4;
B. (x – 1)2 + y2 = 25;
C. ;
D. 3x – y = 2023.
Câu 2. Cho hàm số y = f(x) có đồ thị như hình dưới.
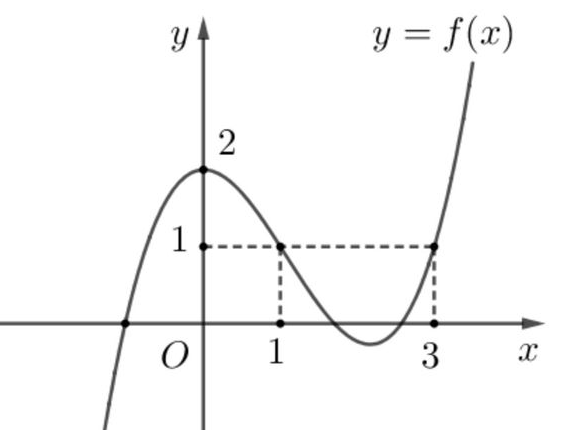
Hàm số trên đồng biến trên khoảng
A. (– ∞; 2);
B. (2; + ∞);
C. (1; 3);
D. (– ∞; 0).
Câu 3. Hàm số có tập xác định là
A. (3; + ∞);
B. [– 3; +∞);
C. (– ∞; 3);
D. ℝ \ {– 3}.
Câu 4. Trong các hàm số sau, hàm số nào là hàm số bậc hai?
A. y = 2x3 – 3x2 + x;
B. y = (2x2)2 – x + 8;
C. y = x3 + x2 + 4x – x3;
D. y = 15 – 4x4 – x2.
Câu 5. Đồ thị của hàm số bậc hai y = x2 + 2x + 8 có trục đối xứng là
A. x = 1;
B. x = – 1;
C. x = 4;
D. x = – 4.
Câu 6. Cho hàm số bậc hai f(x) = 2x2 + 5x + 9. Giá trị nhỏ nhất của hàm số là
A. ;
B. ;
C. ;
D. Không tồn tại.
Câu 7. Biểu thức nào dưới đây không phải là tam thức bậc hai?
A. f(x) = x2 + 8x + 9;
B. f(x) = 3x2 + 10;
C. f(x) = 3x – 1 + x2;
D. f(x) = (x2)2 – x2 + 4.
Câu 8. Cho tam thức bậc hai f(x) = – 2x2 + 8x – 8. Mệnh đề nào sau đây đúng?
A. f(x) < 0 với mọi x ∈ ℝ;
B. f(x) ≥ 0 với mọi x ∈ ℝ;
C. f(x) ≤ 0 với mọi x ∈ ℝ;
D. f(x) > 0 với mọi x ∈ ℝ.
Câu 9. Bất phương trình – x2 + 2x + 3 > 0 có tập nghiệm là
A. (– ∞; – 1) ∪ (3; + ∞);
B. (– 1; 3);
C. [– 1; 3];
D. (– 3; 1).
Câu 10. Phương trình có nghiệm là
A. x = 1;
B. x = 2;
C. x = 3;
D. x = 4.
Câu 11. Số nghiệm của phương trình là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 12. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – 2x + 3y + 10 = 0. Một vectơ chỉ phương của đường thẳng d là
A. ;
B. ;
C. ;
D. .
Câu 13. Phương trình tham số của đường thẳng đi qua hai điểm M(1; – 2) và N(4; 3) là
A. ;
B. ;
C. ;
D. .
Câu 14. Cho đường thẳng d có phương trình tham số: . Phương trình tổng quát của đường thẳng d là
A. 4x – 5y – 7 = 0;
B. 4x + 5y – 17 = 0;
C. 4x – 5y – 17 = 0;
D. 4x + 5y + 17 = 0.
Câu 15. Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
A. ;
B. (– 27; 17);
C. ;
D. (27; – 17).
Câu 16. Với giá trị nào của m thì hai đường thẳng d1: 2x – 3y – 10 = 0 và d2: vuông góc?
A. ;
B. ;
C. ;
D. .
Câu 17. Khoảng cách từ điểm A(– 3; 2) đến đường thẳng ∆: 3x – y + 1 = 0 là
A. ;
B. ;
C. ;
D. .
Câu 18. Góc giữa hai đường thẳng a: 2x + 5y – 2 = 0 và b: 3x – 7y + 3 = 0 bằng
A. 30°;
B. 135°;
C. 60°;
D. 45°.
Câu 19. Phương trình nào sau đây là phương trình đường tròn?
A. x2 + y2 – 4xy + 2x + 8y – 3 = 0;
B. x2 + 2y2 – 4x + 5y – 1 = 0;
C. x2 + y2 – 14x + 2y + 2018 = 0;
D. x2 + y2 – 4x + 5y + 2 = 0.
Câu 20. Đường tròn x2 + y2 – 10y – 24 = 0 có bán kính bằng
A. 49;
B. 7;
C. 1;
D. .
Câu 21. Phương trình đường có tâm là gốc tọa độ O và tiếp xúc với đường thẳng ∆: x + y – 2 = 0 là
A. x2 + y2 = 2;
B. x2 + y2 = ;
C. (x – 1)2 + (y – 1)2 = ;
D. (x – 1)2 + (y – 1)2 = 2.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt đầu ném ra được cho bởi công thức h(t) = – t2 + 2t + 3 (tính bằng mét), t là thời gian (tính bằng giây, t ≥ 0).
a) Tính chiều cao lớn nhất quả bóng đạt được.
b) Hãy tính xem sau bao lâu quả bóng sẽ rơi xuống mặt đất?
Bài 2. (1 điểm) Tìm tất cả các giá trị của tham số m để bất phương trình x2 – 2x + 1 – m2 ≤ 0 nghiệm đúng với mọi x ∈ [1; 2].
Bài 3. (1 điểm) Cho đường tròn (C) có phương trình x2 + y2 – 6x + 2y + 6 = 0 và hai điểm A(1; – 1), B(1; 3).
a) Chứng minh rằng điểm A thuộc đường tròn và điểm B nằm ngoài đường tròn.
b) Viết phương trình tiếp tuyến của (C) tại điểm A.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 10
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức có đáp án - (Đề số 3)
I. Trắc nghiệm (7 điểm)
Câu 1. Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?
A. x + 3y = 7;
B. x2 + y2 = 5;
C. ;
D. .
Câu 2. Cho hàm số dưới dạng bảng như sau:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
1 |
3 |
5 |
7 |
9 |
Giá trị của hàm số y tại x = 3 là
A. 2;
B. 3;
C. 5;
D. 7.
Câu 3. Cho hàm số y = f(x) có đồ thị như hình dưới.
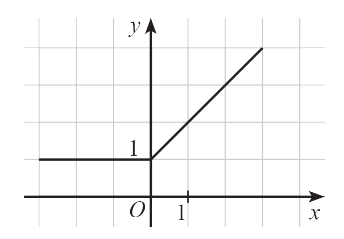
Hàm số trên đồng biến trên khoảng
A. (0; 1);
B. (1; + ∞);
C. (0; + ∞);
D. (– ∞; 0).
Câu 4. Hàm số có tập xác định là
A. (1; 2);
B. [1; 2];
C. {1; 2};
D. ℝ \ {1; 2}.
Câu 5. Cho hàm số . Giá trị của hàm số tại x = 10 là
A. 20;
B. ;
C. ;
D. Không tồn tại.
Câu 6. Trong các hàm số sau, hàm số nào không phải là hàm số bậc hai?
A. y = x2 – 5x + 3;
B. y = 1 – 2x2 + 4x;
C. y = x(x2 + x + 1);
D. y = 7 – x2.
Câu 7. Cho hàm số bậc hai y = 2x2 + 3x – 8. Hoành độ đỉnh của đồ thị hàm số bậc hai này là
A. ;
B. ;
C. ;
D. .
Câu 8. Hàm số bậc hai y = 2 – 3x2 + 4x có hệ số tự do là
A. 2;
B. – 3;
C. 4;
D. – 2.
Câu 9. Cho hàm số bậc hai f(x) = 2x2 – 8x + 7. Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (– ∞; 2), nghịch biến trên khoảng (2; + ∞);
B. Hàm số đồng biến trên khoảng (– ∞; 4), nghịch biến trên khoảng (4; + ∞);
C. Hàm số đồng biến trên khoảng (4; + ∞), nghịch biến trên khoảng (– ∞; 4);
D. Hàm số đồng biến trên khoảng (2; + ∞), nghịch biến trên khoảng (– ∞; 2).
Câu 10. Xác định parabol y = ax2 + c, biết rằng parabol này đi qua hai điểm A(1; 1) và B(2; – 2).
A. y = – x2 + 2;
B. y = x2 + 2;
C. y = 2x2 – 1;
D. y = 2x2 + 1.
Câu 11. Tìm khẳng định đúng trong các khẳng định sau.
A. f(x) = 3x2 + x – 4 là tam thức bậc hai;
B. f(x) = 3x – 5 là tam thức bậc hai;
C. f(x) = 2x3 + 3x – 2 là tam thức bậc hai;
D. f(x) = (x2)2 – x2 + 3 là tam thức bậc hai.
Câu 12. Cho hàm số f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Cho biết dấu của ∆ khi f(x) luôn cùng dấu với hệ số a với mọi x ∈ ℝ.
A. ∆ ≤ 0;
B. ∆ = 0;
C. ∆ > 0;
D. ∆ < 0.
Câu 13. Cho tam thức f(x) = x2 – 8x + 16. Khẳng định nào sau đây là đúng?
A. Phương trình f(x) = 0 vô nghiệm;
B. f(x) > 0 với mọi x ∈ ℝ;
C. f(x) ≥ 0 với mọi x ∈ ℝ;
D. f(x) < 0 khi x < 4.
Câu 14. Trong các phát biểu sau, phát biểu nào sai?
A. x2 – 3x + 2 > 0 khi x ∈ (– ∞; 1) ∪ (2; + ∞);
B. x2 – 3x + 2 ≤ 0 khi x ∈ [1; 2];
C. x2 – 3x + 2 < 0 khi x ∈ [1; 2);
D. x2 – 3x + 2 ≥ 0 khi x ∈ (– ∞; 1] ∪ [2; + ∞).
Câu 15. Tập nghiệm của bất phương trình x2 – 7x + 10 < 0 là
A. S = (– ∞; 2] ∪ [5; + ∞);
C. S = [2; 5];
D. S = (2; 5).
Câu 16. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình là tập nghiệm của phương trình ax2 + bx + c = (dx + e)2;
B. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình dx + e ≥ 0;
C. Mọi nghiệm của phương trình ax2 + bx + c = (dx + e)2 đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình ax2 + bx + c ≥ 0.
Câu 17. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình là tập nghiệm của phương trình ax2 + bx + c = dx2 + ex + f;
B. Tập nghiệm của phương trình là tập nghiệm của phương trình (ax2 + bx + c)2 = (dx2 + ex + f)2;
C. Mọi nghiệm của phương trình ax2 + bx + c = dx2 + ex + f đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình ax2 + bx + c = dx2 + ex + f thỏa mãn bất phương trình ax2 + bx + c ≥ 0 (hoặc dx2 + ex + f ≥ 0).
Câu 18. Số nghiệm của phương trình là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 19. Giá trị nào sau đây là một nghiệm của phương trình?
A. 2;
B. 4;
C. 12;
D. 20.
Câu 20. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
A. ;
B. ;
C. ;
D. .
Câu 21. Điểm nào dưới đây thuộc đường thẳng d: 3x – 2y + 4 = 0?
A. A(1; 2);
B. B(0; 2);
C. C(2; 0);
D. D(2; 1).
Câu 22. Phương trình tham số của đường thẳng ∆ đi qua điểm A(3; 1) và nhận làm vectơ chỉ phương là
A. ;
B. ;
C. ;
D. .
Câu 23. Phương trình tổng quát của đường thẳng d đi qua điểm A(2; – 2) và nhận làm vectơ pháp tuyến là
A. x – y + 2 = 0;
B. – 3x + y + 4 = 0;
C. x – 3y + 4 = 0;
D. x + 3y + 4 = 0.
Câu 24. Cho đường thẳng d có phương trình tham số . Phương trình tổng quát của đường thẳng d là
A. 2x + y – 1 = 0;
B. – 2x + y – 1 = 0;
C. x + 2y + 1 = 0;
D. 2x + 3y – 1 = 0.
Câu 25. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(– 2; 3) và B(4; – 1). Phương trình nào sau đây là phương trình đường thẳng AB?
A. x + y – 3 = 0;
B. y = 2x + 2;
C. ;
D. .
Câu 26. Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: (*).
Khi đó, ∆1 song song với ∆2 khi và chỉ khi
A. hệ (*) có vô số nghiệm;
B. hệ (*) vô nghiệm;
C. hệ (*) có nghiệm duy nhất;
D. hệ (*) có hai nghiệm.
Câu 27. Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0. Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức
A. ;
B. ;
C. ;
D. .
Câu 28. Trong mặt phẳng tọa độ, cho hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0,
với các vectơ pháp tuyến và tương ứng. Khi đó góc φ giữa hai đường thẳng đó được xác định bởi công thức
A. ;
B. ;
C. ;
D. .
Câu 29. Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là
A. 13;
B. – 13;
C. – 1;
D. 1.
Câu 30. Góc giữa hai đường thẳng a: x – y + 7 = 0 và b: x – y – 2 = 0 là
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Câu 31. Phương trình nào sau đây là phương trình đường tròn?
A. 2x2 + y2 – 6x – 6y – 8 = 0;
B. x2 + 2y2 – 4x – 8y – 12 = 0;
C. x2 + y2 – 2x – 8y + 18 = 0;
D. 2x2 + 2y2 – 4x + 6y – 12 = 0.
Câu 32. Đường tròn (x + 1)2 + (y – 2)2 = 16 có bán kính bằng bao nhiêu?
A. 16;
B. 4;
C. 256;
D. 8.
Câu 33. Phương trình nào sau đây là phương trình của đường tròn tâm I(– 1; 2), có bán kính bằng 5?
A. (x – 1)2 + (y + 2)2 = 25;
B. (x + 1)2 + (y + 2)2 = 25;
C. (x + 1)2 + (y – 2)2 = 25;
D. (x – 1)2 + (y – 2)2 = 25.
Câu 34. Phương trình đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 là
A. (x – 3)2 + (y – 4)2 = 9;
B. (x + 3)2 + (y – 4)2 = 9;
C. (x – 3)2 + (y – 4)2 = 3;
D. (x + 3)2 + (y + 4)2 = 3.
Câu 35. Trong mặt phẳng tọa độ, cho đường tròn (C): (x – 2)2 + (y + 2)2 = 5. Tiếp tuyến tại điểm M(1; 0) thuộc đường tròn (C) có phương trình là
A. y = – 2;
B. x = 1;
C. x + 2y – 1 = 0;
D. x – 2y – 1 = 0.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây:
|
Thời gian (s) |
0 |
0,5 |
1 |
2 |
3 |
|
Độ cao (m) |
0 |
28 |
48 |
64 |
48 |
a) Xác định hàm số bậc hai biểu thị độ cao h(m) của quả bóng gofl tính theo thời gian t(s).
b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?
Bài 2. (1 điểm) Cho đường thẳng d1: 2x – y – 2 = 0; d2: x + y + 3 = 0 và điểm M(3; 0). Viết phương trình đường thẳng ∆ đi qua điểm M, cắt d1 và d2 lần lượt tại A và B sao cho M là trung điểm của đoạn AB.
Bài 3. (1 điểm) Cho đường tròn (C): (x – 1)2 + (y – 2)2 = 4 và đường thẳng d: x – y – 1 = 0. Viết phương trình đường tròn (C') đối xứng của (C) qua d. Tìm tọa độ giao điểm của (C), (C').
Đáp án đề thi Giữa học kì 2 Toán 10 Kết nối tri thức - Đề số 3
I. Bảng đáp án trắc nghiệm
|
1. B |
2. C |
3. C |
4. D |
5. B |
6. C |
7. A |
|
8. A |
9. D |
10. A |
11. A |
12. D |
13. C |
14. C |
|
15. D |
16. B |
17. D |
18. B |
19. A |
20. C |
21. B |
|
22. A |
23. D |
24. A |
25. D |
26. B |
27. A |
28. C |
|
29. D |
30. A |
31. D |
32. B |
33. C |
34. A |
35. D |
II. Hướng dẫn giải một số câu trắc nghiệm
Câu 3.
Đáp án đúng là: C
Từ hình vẽ ta thấy đồ thị hàm số y = f(x) đi lên từ trái sang phải trên khoảng (0; + ∞). Vậy hàm số này đồng biến trên khoảng (0; + ∞).
Câu 4.
Đáp án đúng là: D
Biểu thức có nghĩa khi x2 – 3x + 2 ≠ 0 ⇔ x ≠ 1 và x ≠ 2.
Vậy tập xác định của hàm số là D = ℝ \ {1; 2}.
Câu 5.
Đáp án đúng là: B
Ta có: .
Câu 9.
Đáp án đúng là: D
Ta có: .
Vì hệ số a = 2 > 0 nên hàm số f(x) đồng biến trên khoảng (2; + ∞), nghịch biến trên khoảng (– ∞; 2).
Câu 10.
Đáp án đúng là: C
Vì parabol đi qua hai điểm A(1; 1) và B(2; – 2) nên suy ra .
Vậy parabol có phương trình là: y = – x2 + 2.
Câu 18.
Đáp án đúng là: B
Bình phương hai vế của phương trình ta được
4 – 3x2 = 4x2 – 4x + 1.
Sau khi thu gọn ta được 7x2 – 4x – 3 = 0. Từ đó tìm được x = 1 hoặc .
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 1 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 1.
Câu 19.
Đáp án đúng là: A
Cách 1. Thay lần lượt các giá trị ở từng đáp án vào cho đến khi tìm được giá trị thỏa mãn.
Cách 2. Giải phương trình
Bình phương hai vế của phương trình ta được
3x2 – 6x + 1 = x2 – 3.
Rút gọn ta được x2 – 3x + 2 = 0. Từ đó ta tìm được x = 1 hoặc x = 2.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 24.
Đáp án đúng là: A
Đường thẳng d: ⇒ y = – 9 – 2 . (x – 5) ⇔ 2x + y – 1 = 0.
Câu 25.
Đáp án đúng là: D
Bốn phương trình đã cho đều là dạng của phương trình đường thẳng.
Thay lần lượt toa độ của A, B vào từng phương trình ta thấy tọa độ của A và B đều thỏa mãn phương trình ở đáp án D.
Câu 29.
Đáp án đúng là: D
Khoảng cách từ điểm A(1; 1) đến d: 5x – 12y – 6 = 0 là
.
Câu 30.
Đáp án đúng là: A
Đường thẳng a có một vectơ pháp tuyến là ;
Đường thẳng b có một vectơ pháp tuyến là .
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
.
Suy ra góc giữa hai đường thẳng bằng 30°.
Câu 34.
Đáp án đúng là: A
Đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 nên bán kính đường tròn chính là khoảng cách từ tâm I đến đường thẳng ∆.
Ta có: R = d(I, ∆) = .
Vậy phương trình đường tròn cần tìm là: (x – 3)2 + (y – 4)2 = 9.
Câu 35.
Đáp án đúng là: D
Đường tròn (C) có tâm là I(2; – 2). Tiếp tuyến của (C) tại M(1; 0) có vectơ pháp tuyến , nên có phương trình
1(x – 1) – 2(y – 0) = 0 hay x – 2y – 1 = 0.
III. Hướng dẫn giải tự luận
Bài 1. (1 điểm)
a) Xét hàm số bậc hai biểu thị độ cao h phụ thuộc thời gian t có dạng h(t) = at2 + bt + c, trong đó a ≠ 0. Theo đề bài:
Với t = 0, h = 0, ta có: c = 0 nên h(t) = at2 + bt. Khi đó:
+ Với t = 1, h = 48, ta có: a . 12 + b . 1 = 48 ⇔ a + b = 48.
+ Với t 2, h = 64, ta có: a . 22 + b . 2 = 64 ⇔ 4a + 2b = 64.
Giải hệ phương trình . Suy ra h(t) = – 16t2 + 64t.
Thay các giá trị tương ứng còn lại của bảng vào công thức trên, ta thấy phù hợp.
Vậy hàm số bậc hai cần tìm là h(t) = – 16t2 + 64t.
b) Bóng chạm đất khi h(t) = 0 ⇔ – 16t2 + 64t = 0.
Suy ra t = 0 hoặc t = 4.
Vậy sau 4 giây kể từ khi vận động viên đánh bóng thì bóng lại chạm đất.
Bài 2. (1 điểm)
Gọi tọa độ các điểm A, B và M là A(xA; yA); B(xB; yB) và M(xM; yM).
Vì A thuộc d1 nên 2xA – yA – 2 = 0. Suy ra yA = 2xA – 2.
Vì B thuộc d2 nên xB + yB + 3 = 0. Suy ra yB = – xB – 3.
Do M là trung điểm của đoạn AB nên
.
Suy ra .
Đường thẳng ∆ đi qua điểm A và điểm M.
Ta có: .
Đường thẳng ∆ đi qua M(3; 0) và có một vectơ pháp tuyến là nên có phương trình là
8(x – 3) – (y – 0) = 0 hay 8x – y – 24 = 0.
Bài 3. (1 điểm)
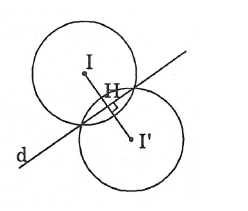
(C) có tâm I(1; 2), bán kính R = 2.
Phương trình đường thẳng ∆ đi qua I, vuông góc với d có dạng x + y + m = 0.
I (1; 2) ∈ ∆, suy ra 1 + 2 + m = 0 ⇒ m = – 3.
Do đó, phương trình đường thẳng ∆: x + y – 3 = 0.
Gọi H là giao điểm của ∆ và d. Tọa độ của H là nghiệm của hệ phương trình
Từ đó tìm được H(2; 1).
Chứng minh được H là trung điểm của II' với I' là tâm của (C'). Suy ra I'(3; 0)
Vì (C), (C') đối xứng nhau qua d nên R = R'.
Vậy phương trình (C'): (x – 3)2 + y2 = 4.
Tọa độ giao điểm của (C), (C') là nghiệm của hệ phương trình:
là giao điểm của (C), (C').
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 10
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 10 Kết nối tri thức có đáp án - (Đề số 4)
I. Trắc nghiệm (7 điểm)
Câu 1. Cho bảng giá trị sau:
|
x |
1 |
2 |
3 |
4 |
|
y |
6 |
9 |
15 |
21 |
Khẳng định nào sau đây là đúng?
A. y là hàm số của x, f(2) = 1;
B. y là hàm số của x, f(2) = 9;
C. x là hàm số của y, f(2) = 9;
D. x là hàm số của y, f(2) = 1.
Câu 2. Trong các hàm số sau, hàm số nào đồng biến trên ℝ?
A. y = 1 – 2x;
B. y = 3x + 2;
C. y = x2 + 2x – 1;
D. y = – 2(2x – 3).
Câu 3. Hàm số có tập xác định là
A. ;
B. (– 3; +∞);
C. ;
D. ℝ \ .
Câu 4. Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào trong các hàm số sau.
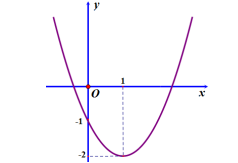
A. y = x2 + 2x – 1;
B. y = x2 + 2x – 2;
C. y = 2x2 – 4x – 2;
D. y = x2 – 2x – 1.
Câu 5. Cho parabol (P): y = 3x2 – 2x + 1. Điểm nào sau đây là đỉnh của (P)?
A. I(0; 1);
B. I;
C. I;
D. I.
Câu 6. Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao 1 m sau đó 1 giây nó đạt độ cao 10 m và 3,5 giây nó ở độ cao 6,25 m. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét?
A. 11 m;
B. 12 m;
C. 13 m;
D. 14 m.
Câu 7. Tam thức nào sau đây luôn dương với mọi giá trị của x?
A. x2 – 10x + 2;
B. x2 – 2x – 10;
C. x2 – 2x + 10;
D. – x2 + 2x + 10.
Câu 8. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0) và ∆ = b2 – 4ac. Cho biết dấu của ∆ khi f(x) luôn cùng dấu với hệ số a với mọi x ∈ ℝ.
A. ∆ < 0;
B. ∆ ≥ 0;
C. ∆ > 0;
D. ∆ = 0.
Câu 9. Số nghiệm nguyên của bất phương trình 2x2 – 3x – 15 ≤ 0 là
A. 5;
B. 6;
C. 7;
D. 8.
Câu 10. Phương trình có hai nghiệm là a và b. Khi đó giá trị của biểu thức T = a + b là
A. 32;
B. 38;
C. 35;
D. 3.
Câu 11. Số nghiệm của phương trình là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 12. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: . Một vectơ pháp tuyến của đường thẳng d là
A. ;
B. ;
C. ;
D. .
Câu 13. Phương trình tham số của đường thẳng đi qua hai điểm A(2; – 1) và B(2; 5) là
A. ;
B. ;
C. ;
D. .
Câu 14. Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 2). Gọi A và B là hình chiếu của M lên Ox, Oy. Phương trình đường thẳng AB là
A. x + 2y – 1 = 0;
B. 2x + y + 2 = 0;
C. 2x + y – 2 = 0;
D. x + y – 3 = 0.
Câu 15. Đường thẳng d: 51x – 30y + 11 = 0 đi qua điểm nào sau đây?
A. ;
B. ;
C. ;
D. .
Câu 16. Cho hai đường thẳng d1: 2x + 3y + 15 = 0 và d2: x – 2y – 3 = 0. Khẳng định nào sau đây đúng?
A. d1 và d2 cắt nhau và không vuông góc với nhau;
B. d1 và d2 song song với nhau;
C. d1 và d2 trùng nhau;
D. d1 và d2 vuông góc với nhau.
Câu 17. Khoảng cách giữa hai đường thẳng song song ∆1: 6x – 8y + 3 = 0 và ∆2: 3x – 4y – 6 = 0 bằng
A. ;
B. ;
C. 2;
D. .
Câu 18. Xác định tất cả các giá trị của a để góc tạo bởi đường thẳng và đường thẳng 3x + 4y – 2 = 0 bằng 45°.
A. a = 1, a = – 14;
B. a = , a = – 14;
C. a = – 2, a = – 14;
D. a = , a = 14.
Câu 19. Phương trình nào sau đây không là phương trình đường tròn?
A. x2 + y2 = 4;
B. 2x2 + 3y2 + 2x + 3y = 9;
C. x2 + y2 + 2x – 1 = 0;
D. x2 + y2 + 4y + 3 = 0.
Câu 20. Tọa độ tâm I và bán kính R của đường tròn (C): x2 + y2 – 2x + 4y + 1 = 0 là
A. I(– 1; 2), R = 4;
B. I(1; – 2), R = 2;
C. I(– 1; 2), R = ;
D. I(1; – 2), R = 4.
Câu 21. Cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0 và điểm A(1; 5). Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn (C) tại điểm A?
A. y – 5 = 0;
B. y + 5 = 0;
C. x + y – 5 = 0;
D. x – y – 5 = 0.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Giải các bất phương trình sau:
a) – x2 + 2x + 5 > 2;
b) (1 – 2x)(x2 – x – 1) > 0.
Bài 2. (1 điểm) Một cửa hàng bán bưởi Phúc Trạch của Hà Tĩnh với giá bán mỗi quả là 50 000 đồng. Với giá bán này thì mỗi ngày cửa hàng chỉ bán được 40 quả. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5 000 đồng thì số bưởi bán tăng thêm được 10 quả. Xác định giá bán để cửa hàng thu được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu cho mỗi quả là 30 000 đồng.
Bài 3. (1 điểm) Cho P(3; 0) và hai đường thẳng d1: 2x – y – 2 = 0 và d2: x + y + 3 = 0. Gọi d là đường thẳng qua P và cắt d1, d2 sao cho PA = PB. Viết phương trình đường thẳng d.
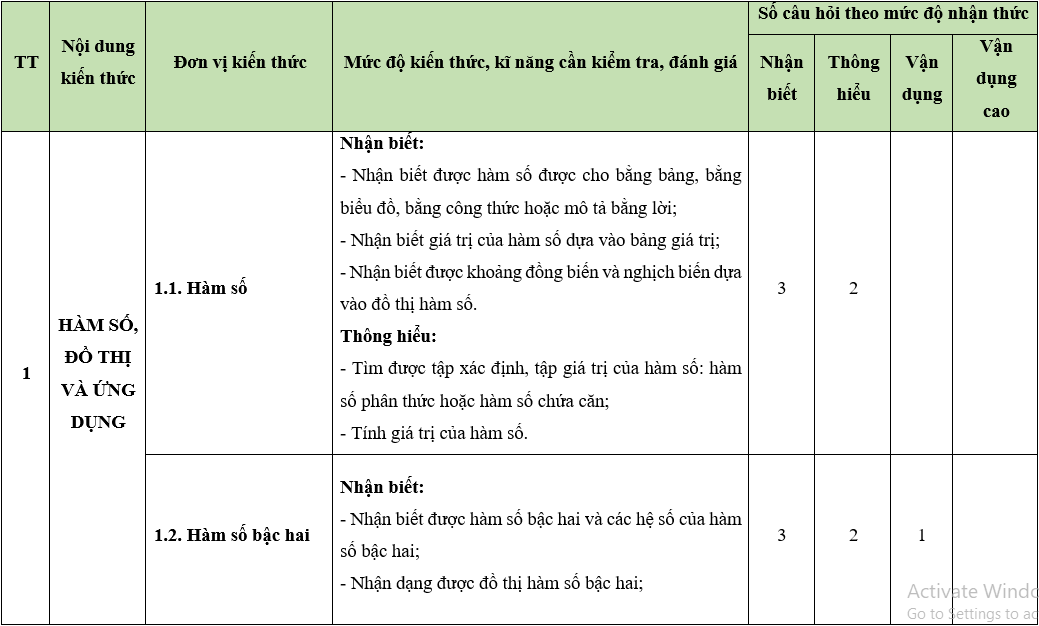
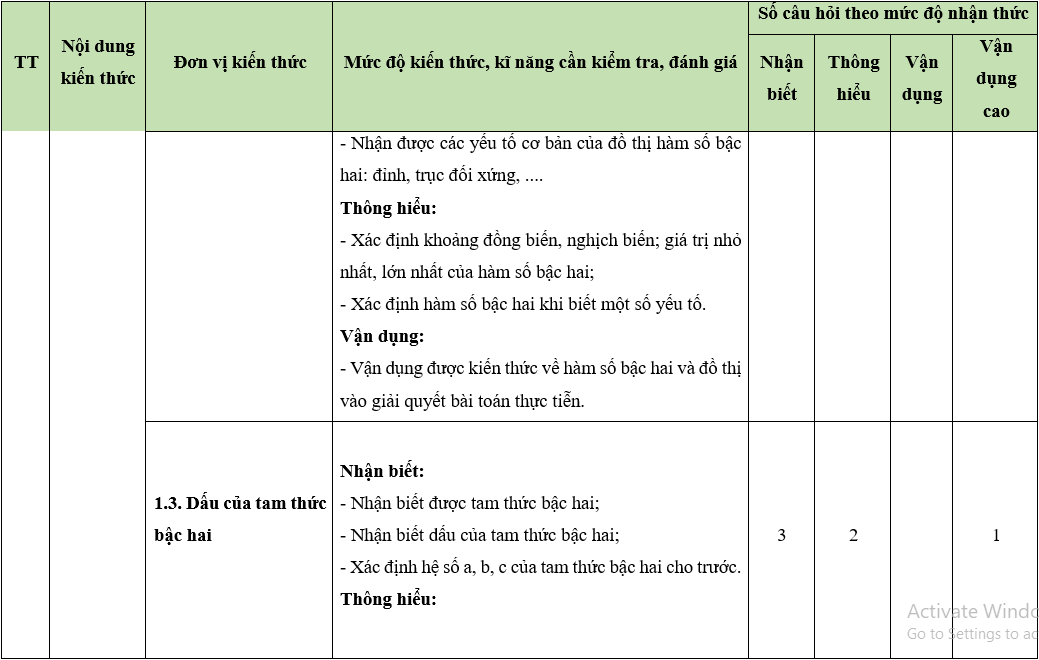
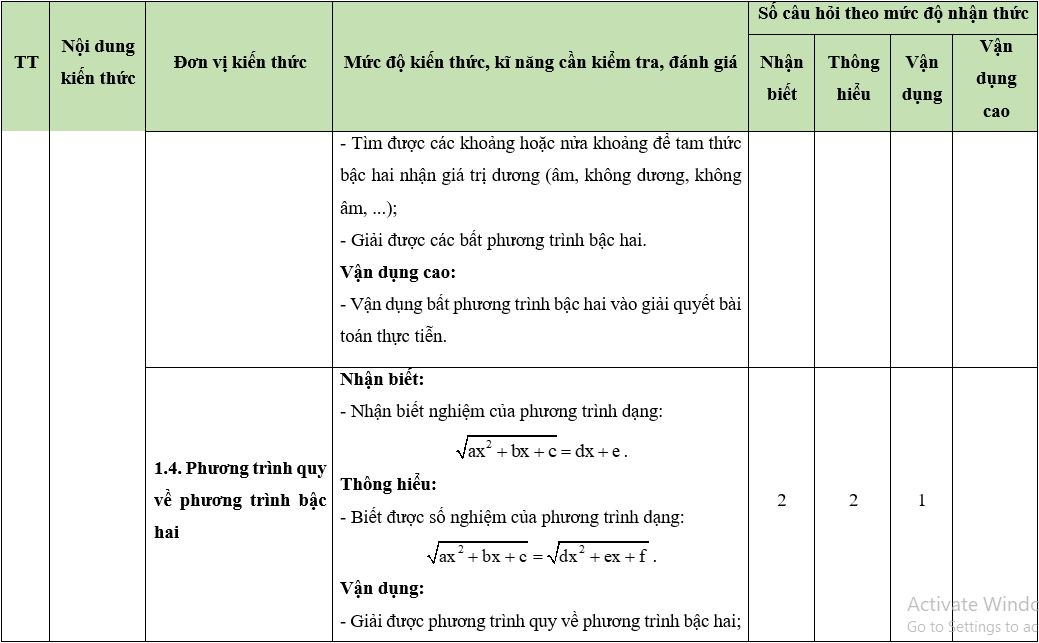
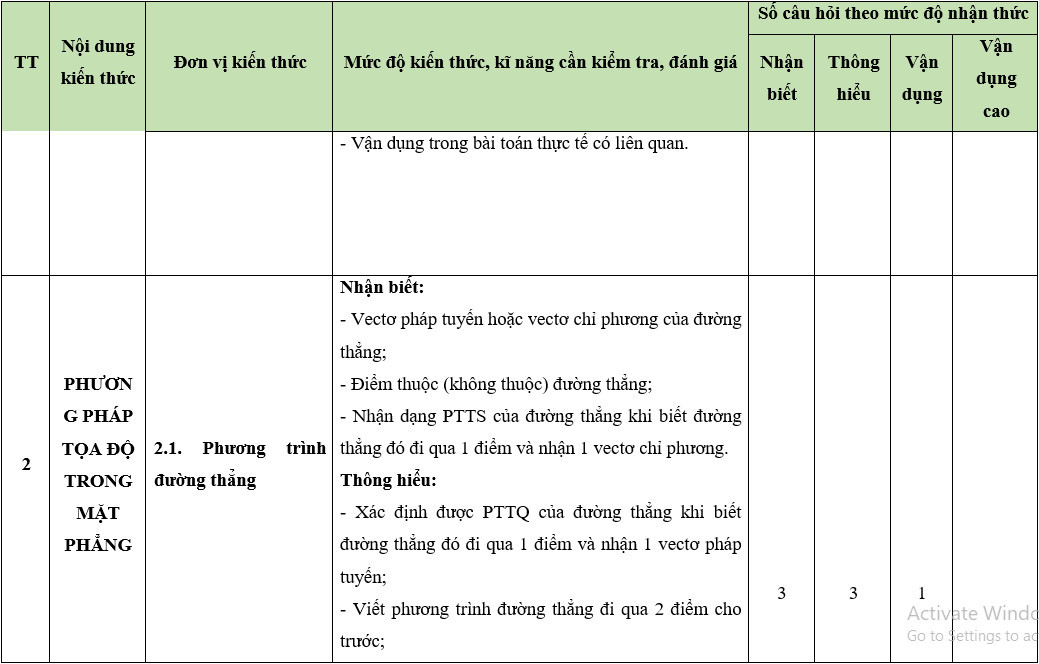
A. Ma trận đề thi giữa học kì 2
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 35 câu (70%)
Câu hỏi tự luận : 3 câu (30%)
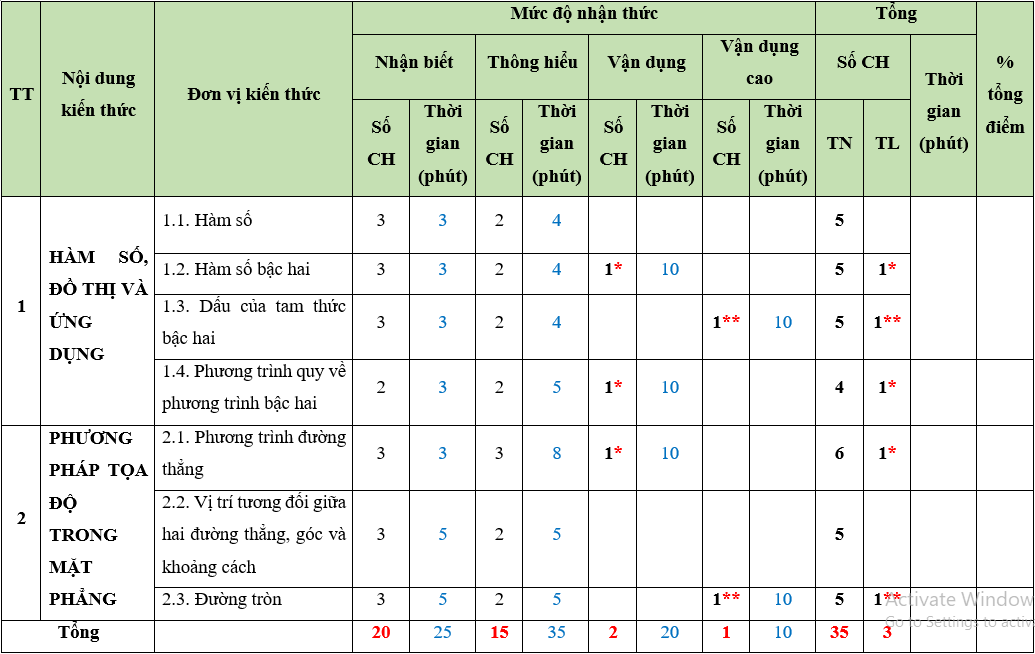
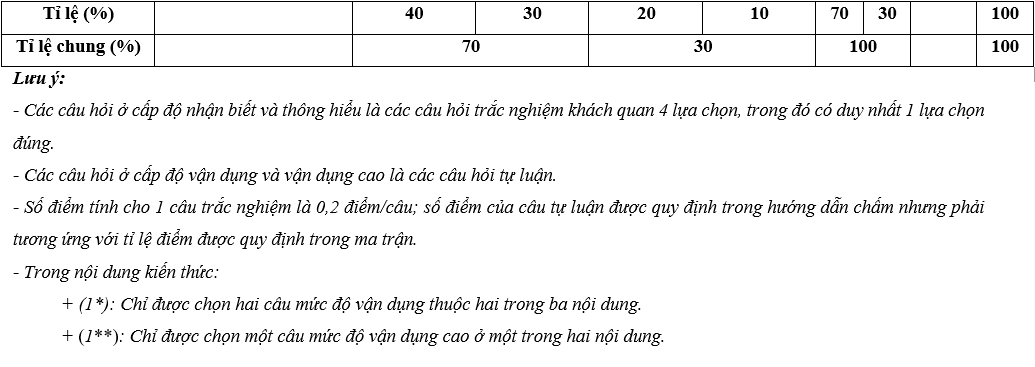
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA GIỮA HỌC KÌ 2
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 90 phút