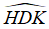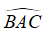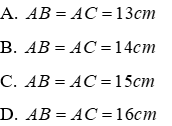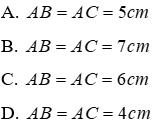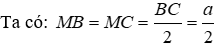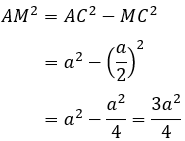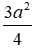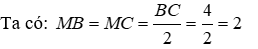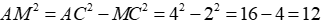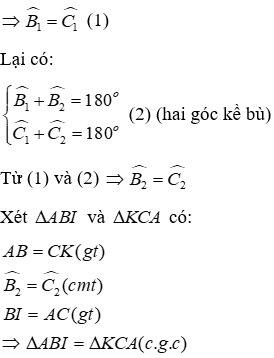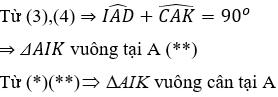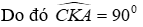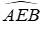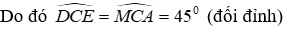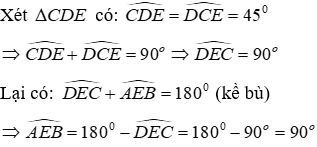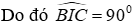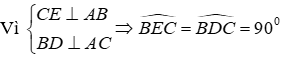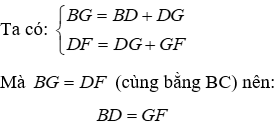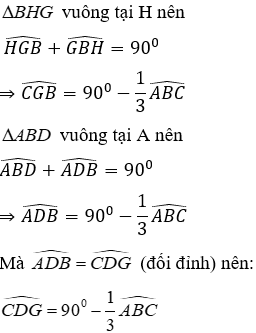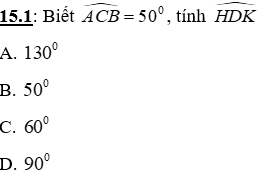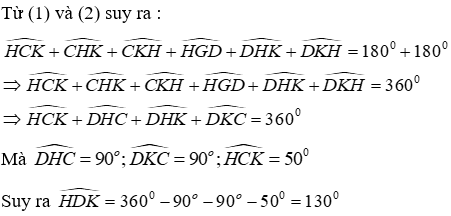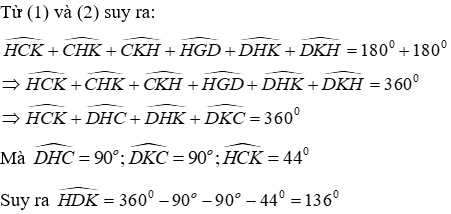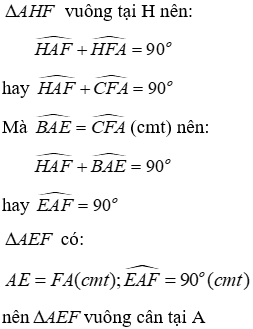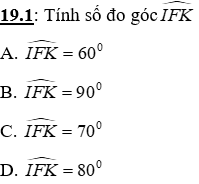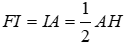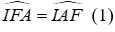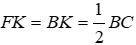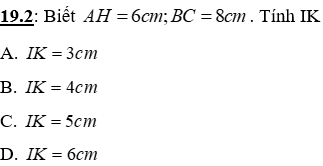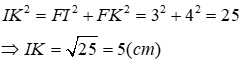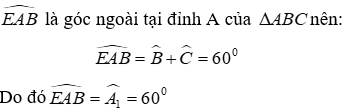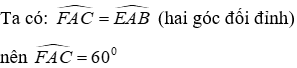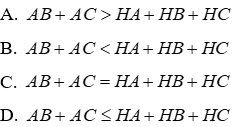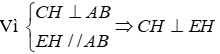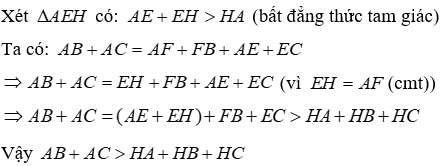Toán học 7 Bài 59: Tính chất ba đường cao của tam giác
Lý thuyết tổng hợp Toán học lớp 7 Bài 59: Tính chất ba đường cao của tam giác, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 59: Tính chất ba đường cao của tam giác
A. Lý thuyết
1. Đường cao của tam giác
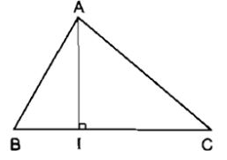
• Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.
Ví dụ: Đoạn thẳng AI là một đường cao của tam giác ABC, còn nói AI là đường cao xuất phát từ đỉnh A (của tam giác ABC).
• Mỗi tam giác có ba đường cao.
2. Tính chất ba đường cao của một tam giác
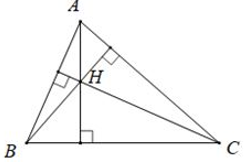
Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
Ví dụ: H là giao điểm ba đường cao của tam giác ABC. H là trực tâm của tam giác ABC
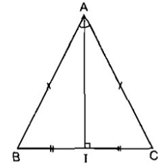
3. Về các đường cao, trung tuyến, trung trực, phân giác của tam giác cân
Tính chất của tam giác cân: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó.
Nhận xét:
Trong một tam giác, nếu hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này) trùng nhau thì tam giác đó là một tam giác cân
Đặc biệt đối với tam giác đều, từ tính chất trên suy ra: Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.
4. Ví dụ
Ví dụ :Cho tam giác nhọn ABC có hai đường cao AH và BK cắt nhau tại D. Biết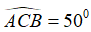 
, tính 
Hướng dẫn giải:
5. Bài tập vận dụng
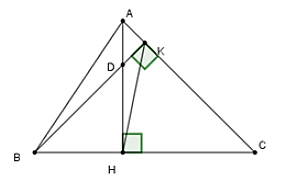
Bài 1: Cho hai đường thẳng xx' và yy' cắt nhau tại O. Trên Ox và Ox’ lần lượt lấy các điểm A và C; trên Oy và Oy’ lần lượt lấy các điểm B, D sao cho OA = OA, OC = OD. Gọi M, N lần lượt là trung điểm của AB, CD
Chứng minh M, O, N thẳng hàng.
Hướng dẫn giải:
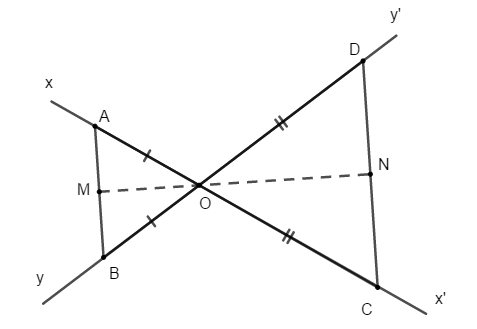
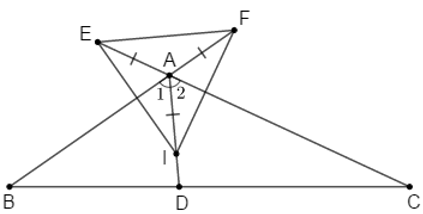
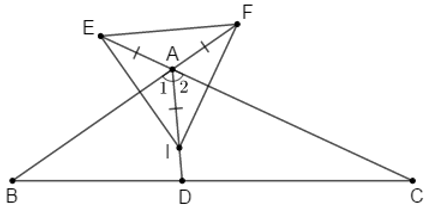
Bài 2:Cho tam giác ABC cân tại A. Qua A kẻ đường thẳng d song song với đáy BC. Các đường phân giác của góc B và góc C lần lượt cắt d tại E và F. Chứng minh rằng:
a) d là phân giác ngoài của góc A
b) AE = AF
Hướng dẫn giải:
b) Gọi I là giao điểm của hai tia phân giác CF và BE trong tam giác ABC
Nên I là giao điểm của ba đường phân giác trong tam giác ABC
Suy ra AI là tai phân giác của góc 
Mà tam giác ABC cân tại A
Nên AI là đường trung trực ứng với cạnh BC của tam giác ABC
B. Bài Tập
Câu 1: Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em chọn phát biểu đúng:
A. H là trọng tâm của ΔABC
B. H là tâm đường tròn nội tiếp ΔABC
C. CH là đường cao của ΔABC
D. CH là đường trung trực của ΔABC
Lời giải:
Vì hai đường cao AM và BN cắt nhau tại H nên CH là đường cao của ΔABC và H là trực tâm của tam giác ABC nên A, B, C sai, C đúng
Đáp án cần chọn là: C
Câu 2: Trực tâm của tam giác là:
A. ba đường trung tuyến.
B. ba đường phân giác.
C. ba đường cao.
D. ba đường trung trực.
Lời giải:
Trực tâm của tam giác là giao của ba đường cao.
Đáp án cần chọn là: C
Câu 3: Cho tam giác ABC cân tại A có AM là đường trung tuyến khi đó:
A. AM ⊥ BC
B. AM là đường trung trực của BC
C. AM là đường phân giác của góc BAC
D. Cả a, b, c đều đúng
Lời giải:
Vì tam giác ABC cân tại A có AM là đường trung tuyến nên AM cũng là đường cao, đường trung trực và đường phân giác của tam giác ABC.
Đáp án cần chọn là: D
Câu 4: Cho tam giác ABC có AM là đường phân giác đồng thời cũng là đường cao, khi đó tam giác ABC là tam giác gì?
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông cân
Lời giải:
Vì tam giác ABC cân tại A có AM là đường phân giác đồng thời cũng là đường cao nên là tam giác cân
Đáp án cần chọn là: B
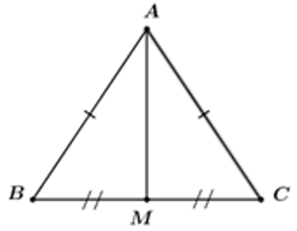
Câu 5: Cho cân tại A, trung tuyến AM. Biết BC = 24cm, AM = 5cm. Tính độ dài các cạnh AB và AC
Lời giải:
Vì ΔABC cân tại A(gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó
Vì AM là trung tuyến của ΔABC nên M là trung điểm của BC
Đáp án cần chọn là: A
Câu 6: Cho ΔABC cân tại A, trung tuyến AM. Biết BC = 6cm, AM = 4cm. Tính độ dài các cạnh AB và AC
Lời giải:
Vì ΔABC cân tại A(gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó
Vì AM là trung tuyến của ΔABC nên M là trung điểm của BC
Đáp án cần chọn là: A
Câu 7: Đường cao của tam giác đều cạnh a có bình phương độ dài là
Lời giải:
Xét tam giác ABC đều cạnh AB = AC = BC = a có AM là đường trung tuyến suy ra AM cũng là đường cao của tam giác ABC hay AM ⊥ BC tại M
Xét tam giác AMC vuông tại M, theo định lí Pytago ta có:
Vậy bình phương độ dài đường cao của tam giác đều cạnh a là 
Đáp án cần chọn là: A
Câu 8: Đường cao của tam giác đều cạnh 4 có bình phương độ dài đường cao là
A. 16
B. 12
C. 14
D. 10
Lời giải:
Xét tam giác ABC đều cạnh AB = AC = BC = 4 có AM là đường trung tuyến suy ra AM cũng là đường cao của tam giác ABC hay AM ⊥ BC tại M
Xét tam giác AMC vuông tại M, theo định lí Pytago ta có:
Vậy bình phương độ dài đường cao của tam giác đều cạnh 4 là 12
Đáp án cần chọn là: B
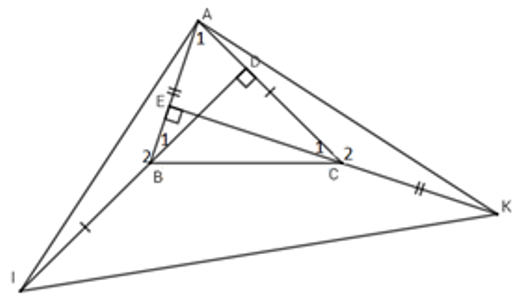
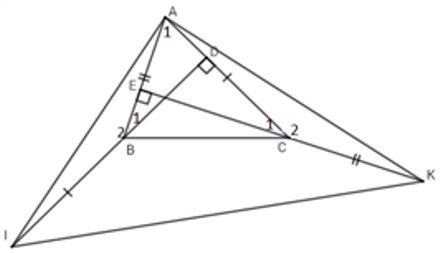
Câu 9: Cho ΔABC nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB
Lời giải:
Xét ΔvABD có: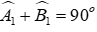 
(trong tam giác vuông 2 góc nhọn phụ nhau )
Xét ΔvAEC có: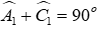 
(trong tam giác vuông2 góc nhọn phụ nhau )
Đáp án cần chọn là: D
9.2: ΔAIK là tam giác gì?
A. ΔAIK là tam giác cân tại B
B. ΔAIK là tam giác vuông cân tại A
C. ΔAIK là tam giác vuông
D. ΔAIK là tam giác đều
Lời giải:
Ta có: AI = AK (cmt) ⇒ ΔAIK cân tại A (*)
(hai góc tương ứng)
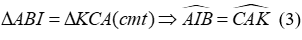
Xét ΔvAID có: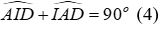 
(trong tam giác vuông2 góc nhọn phụ nhau )
Đáp án cần chọn là: B
Câu 10: Cho ΔABC vuông cân tại B. Trên cạnh AB lấy điểm H. Trên tia đối của tia BC lấy điểm D sao cho BH = BD
10.1: Chọn câu đúng
Lời giải:
Đáp án cần chọn là: A
10.2: Gọi CH cắt AD tại K. Tính số đo góc CKA
Lời giải:
Gọi I là giao điểm của DH và AC
Sử dụng kết quả câu trước ta có: DI ⊥ AC
Xét ΔADC có: AB ⊥ DC;DI ⊥ AC nên H là trực tâm của ΔADC
Suy ra CK là đường cao thứ ba của ΔADC hay CK ⊥ AD
Đáp án cần chọn là: D
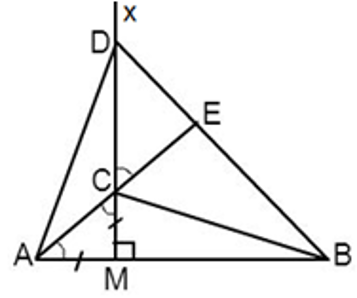
Câu 11: Cho đoạn thẳng AB và điểm M nằm giữa A và B (MA < MB). Vẽ tia Mx vuông góc với AB, trên đó lấy hai điểm C và D sao cho MA = MC, MD = MB. Tia AC cắt BD ở E. Tính 
Lời giải:
Xét ΔAMC có: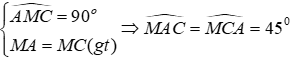 
(tính chất tam giác cân)
Xét ΔBMD có: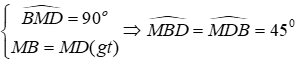 
(tính chất tam giác cân)
Đáp án cần chọn là: D
Câu 12: Cho tam giác ABC vuông cân tại A. Trên cạnh AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AE = AD. Kéo dài CD cắt BE tại I. Tính số đo góc BIC
Lời giải:
Xét ΔBCE có: BA⊥EC;EK⊥BC nên D là trực tâm của ΔBCE
Suy ra CI là đường cao thứ ba của ΔBCE hay CI⊥BE
Đáp án cần chọn là: D
Câu 13: Cho ΔABC cân tại A, hai đường cao BD và CE cắt nhau tại I. Tia AI cắt BC tại M. Khi đó ΔMED là tam giác gì?
A. Tam giác cân
B. Tam giác vuông cân
C. Tam giác vuông
D. Tam giác đều
Lời giải:
Xét ΔABC có BD và CE là đường cao cắt nhau tại I suy ra AI là đường cao của tam giác đó
Mà AI cắt BC tại M nên AM⊥BC
Vì ΔABC cân tại A (gt) nên AM là đường cao cũng chính là đường trung trực của tam giác đó (tính chất tam giác cân)
⇒ BM = MC (tính chất đường trung tuyến)
Xét ΔvBEC có M là trung điểm của BC nên suy ra EM là trung tuyến của ΔvBEC
(tính chất đường trung tuyến của tam giác vuông)
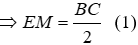
Xét ΔvBDC có M là trung tuyến của BC nên suy ra DM là trung tuyến của ΔvBDC
(tính chất đường trung tuyến của tam giác vuông)
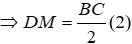
Từ (1)(2) ⇒ EM = DM ⇒ ΔEMD cân tại M (dấu hiệu nhận biết tam giác cân)
Đáp án cần chọn là: A
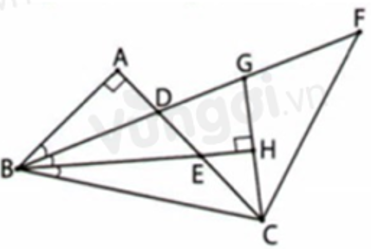
Câu 14: Cho ΔABC vuông tại A, trên cạnh AC lấu các điểm D,E sao cho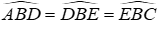 
. Trên tia đối của tia DB lấy điểm F sao cho DF = BC. Tam giác CDF là tam giác gì?
A. Tam giác cân tại F
B. Tam giác vuông tại D
C. Tam giác cân tại D
D. Tam giác cân tại C
Lời giải:
Trên đoạn BF lấy điểm G sao cho BG = BC khi đó G nằm giữa D và F
ΔBCG cân tại B,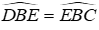 
nên BE là phân giác đồng thời là đường cao của ΔBCG
Gọi H là giao của BE và GC nên BH⊥GC
Đáp án cần chọn là: A
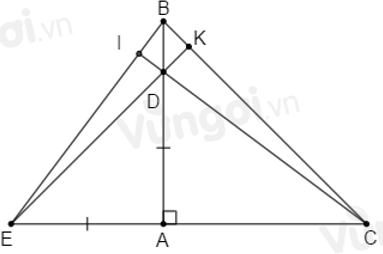
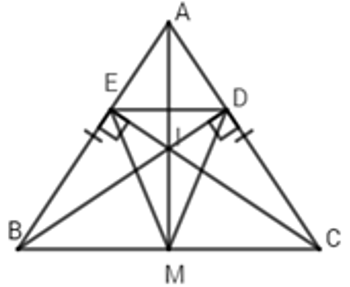
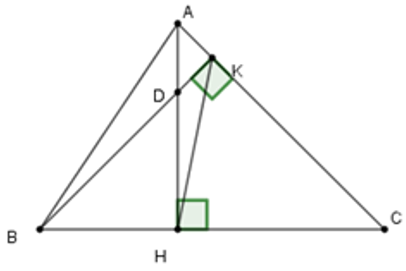
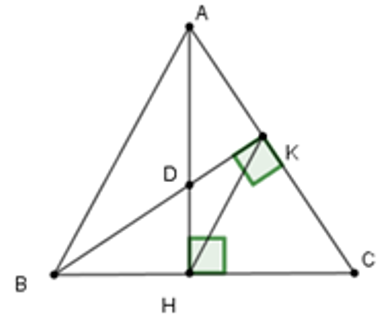
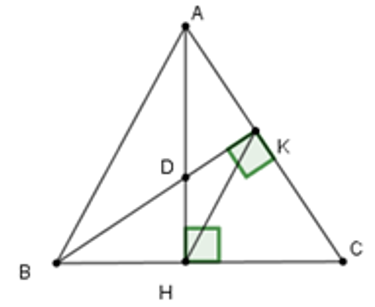
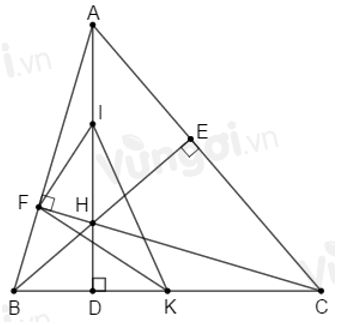
Câu 15: Cho tam giác nhọn ABC có hai đường cao AH và BK cắt nhau tại D
Lời giải:
Xét tam giác CHK có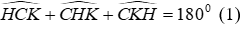 
(định lí tổng ba góc trong tam giác)
Xét tam giác DHK có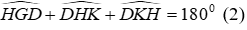 
(định lí tổng ba góc trong tam giác)
Đáp án cần chọn là: A
15.2: Nếu DA = DB thì tam giác ABC là tam giác
A. Cân tại A
B. Cân tại B
C. Cân tại C
D. Đều
Lời giải:
Nếu DA = DB thì tam giác DAB cân tại D suy ra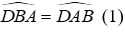 
(tính chất tam giác cân)
Đáp án cần chọn là: C
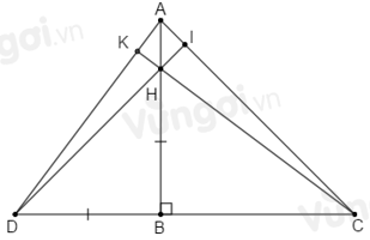
Câu 16: Cho tam giác nhọn ABC có hai đường cao AH và BK cắt nhau tại D
Lời giải:
Xét tam giác CHK có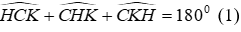 
(định lí tổng ba góc trong tam giác)
Xét tam giác DHK có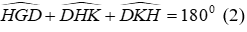 
(định lí tổng ba góc trong tam giác)
Đáp án cần chọn là: C
16.2: Nếu DA = DB và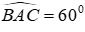 
thì tam giác ABC là tam giác
A. Cân tại A
B. Cân tại B
C. Cân tại C
D. Đều
Lời giải:
Nếu thì tam giác DAB cân tại D suy ra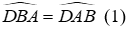 
(tính chất tam giác cân)
Đáp án cần chọn là: D
Câu 17: Cho ΔABC có vuông tại A, đường cao AH, phân giác AD. Gọi I, J lần lượt là giao điểm các phân giác của ΔABH, ΔACH, E là giao điểm của đường thẳng BI và AJ. Chọn câu đúng
A. ΔABE là tam giác vuông tại E
B. ΔABE là tam giác vuông tại A
C. ΔABE là tam giác vuông tại B
D. ΔABE là tam giác đều
Lời giải:
Đáp án cần chọn là: A
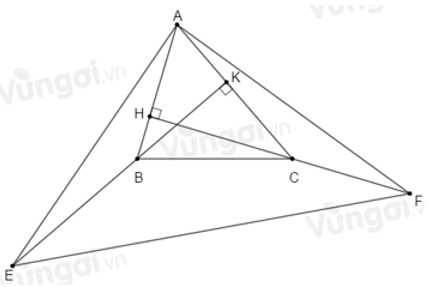
Câu 18:Cho ΔABC có góc A nhọn. Kẻ hai đường cao BK và CH. Trên tia đối của tia BK lấy điểm E so cho BE = AC. Trên tia đối của CH lấy điểm F sao cho CF = AB. Chọn câu đúng
Lời giải:
Đáp án cần chọn là: C
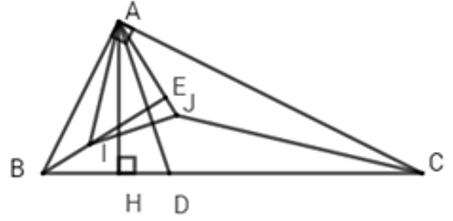
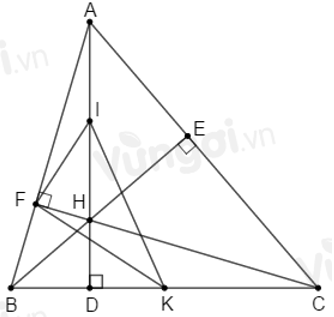
Câu 19: Cho tam giác ABC có các đường cao BE; CF cắt nhau tại H. Gọi I là trung tâm đoạn AH và K là trung điểm cạnh BC
Lời giải:
H là giao của hai đường cao BE; CF nên H là trực tâm của ΔABC
Gọi D là giao của AH và BC nên AD ⊥ BC
Xét ΔAFH vuông tại F, đường trung tuyến FI nên 
(trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Do đó ΔFAI cân tại I suy ra 
Xét ΔBFC vuông tại F, đường trung tuyến FK nên 
(trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Đáp án cần chọn là: B
Lời giải:
Áp dụng định lí Pytago vào tam giác vuông IFK ta có:
Đáp án cần chọn là: C
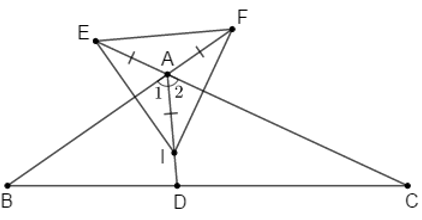
Câu 20: Cho tam giác ABC có: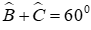 
. Trên đường phân giác AD của góc A lấy điểm I. Trên tia đối của tia AB lấy điểm F sao cho AF = AI. Trên tia đối của tia AC lấy điểm E sao cho AE = AI
20.1: Chọn câu sai
A. AB là đường trung trực của đoạn IE
B. AC là đường trung trực của đoạn IF
C. ΔEAI cân tại A
D. ΔEAI cân tại I
Lời giải:
ΔEAI cân tại A (vì AE = AD(gt)) mà AB là phân giác nên AB là đường trung trực của IE
ΔFAI cân tại I (vì AI = AF(gt)) mà AC là phân giác nên AC là đường trung trực của IF
Vậy cả A, B, C đều đúng
Đáp án cần chọn là: D
20.2: Tam giác IEF là tam giác gì?
A. Tam giác vuông
B. Tam giác vuông cân
C. Tam giác đều
D. Tam giác tù
Lời giải:
Sử dụng kết quả câu trước ta có: AB là đường trung trực IE,AC là đường trung trực cả IF
Vì E nằm trên đường trung trực của IF nên EF = EI (tính chất đường trung trực) (1)
Vì F nằm trên đường trung trực của IE nên EF = FI (tính chất đường trung trực) (2)
Từ (1) và (2) suy ra EF = EI = FI do đó: ΔIEF là tam giác đều
Đáp án cần chọn là: C
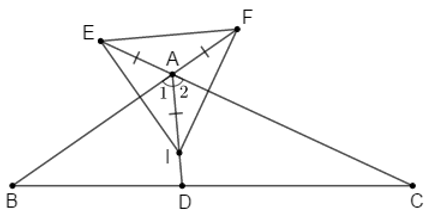
Câu 21: Cho tam giác ABC có: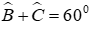 
. Trên đường phân giác AD của góc A lấy điểm I. Trên tia đối của tia AB lấy điểm F sao cho . Trên tia đối của tia AC lấy điểm E sao cho
20.1: Chọn câu đúng nhất
A. AB là đường trung trực của đoạn IE
B. AC là đường trung trực của đoạn IF
C. ΔEAI cân tại A
D. Cả A, B, C đều đúng
Lời giải:
∆EAI cân tại A (vì AE = AD (gt)) mà AB là phân giác nên AB là đường trung trực của IE
∆FAI cân tại I (vì AI = AF (gt)) mà AC là phân giác nên AC là đường trung trực của IF
Vậy cả A, B, C đều đúng
Đáp án cần chọn là: D
20.2: Tam giác IEF là tam giác gì?
A. Tam giác vuông
B. Tam giác vuông cân
C. Tam giác đều
D. Tam giác tù
Lời giải:
Sử dụng kết quả câu trước ta có: AB là đường trung trực IE, AC là đường trung trực cả IF
Vì E nằm trên đường trung trực của IF nên EF = EI (tính chất đường trung trực) (1)
Vì F nằm trên đường trung trực của IE nên EF = FI (tính chất đường trung trực) (2)
Từ (1) và (2) suy ra EF = EI = FI do đó: ΔIEF là tam giác đều
Đáp án cần chọn là: C
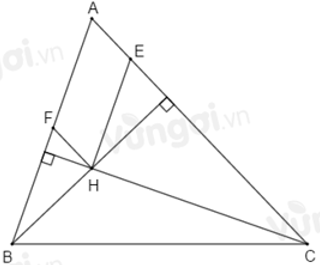
Câu 22: Cho tam giác ABC nhọn có trực tâm H. Chọn câu đúng
Lời giải:
Qua H kẻ đường thẳng song song với AC cắt AB tại F, kẻ đường thẳng song song với AB cắt AC tại E
Ta có: BF; BH lần lượt là đường xiên và đường vuông góc kẻ từ B đến FH nên BF > BH (quan hệ đường xiên - đường vuông góc)
Ta có: CE; CH lần lượt là đường xiên và đường vuông góc kẻ từ C đến FH nên CE > CH (quan hệ đường xiên - đường vuông góc)
Đáp án cần chọn là: A
Bài viết liên quan
- Toán học 7 Bài 55: Tính chất tia phân giác của một góc
- Toán học 7 Bài 56: Tính chất ba đường phân giác của tam giác
- Toán học 7 Bài 57: Tính chất đường trung trực của một đoạn thẳng
- Toán học 7 Bài 58: Tính chất ba đường trung trực của tam giác
- Toán học 7 Bài 60: Tổng hợp lý thuyết Chương 3 Hình học 7
