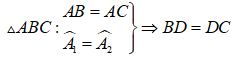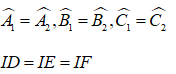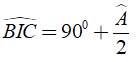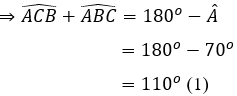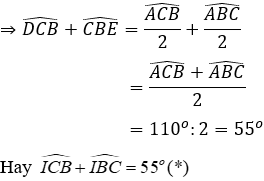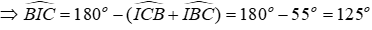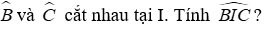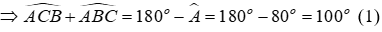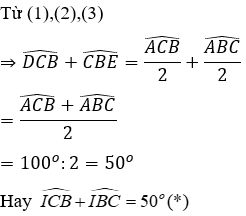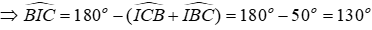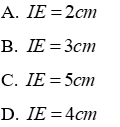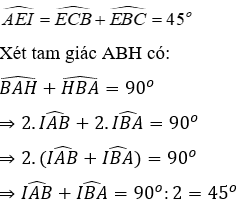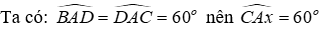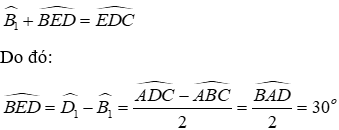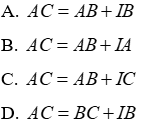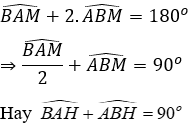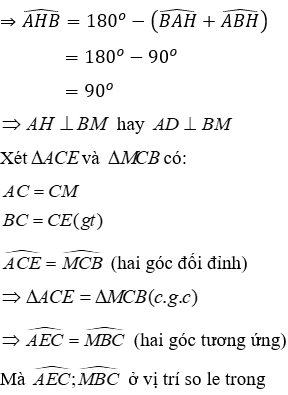Toán học 7 Bài 56: Tính chất ba đường phân giác của tam giác
Lý thuyết tổng hợp Toán học lớp 7 Bài 56: Tính chất ba đường phân giác của tam giác, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 56: Tính chất ba đường phân giác của tam giác
A. Lý thuyết
1. Đường phân giác của tam giác
• Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm M, khi đó đoạn thẳng AM được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC. Ta cũng gọi đường thẳng AM là đường phân giác của tam giác ABC.
• Mỗi tam giác có ba đường phân giác.
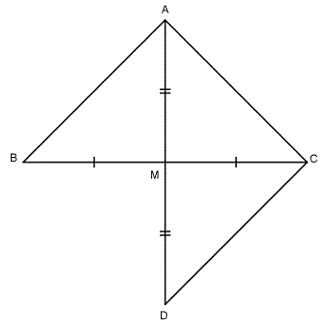
Tính chất: Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến ứng với cạnh đáy.
2. Tính chất ba đường phân giác của tam giác
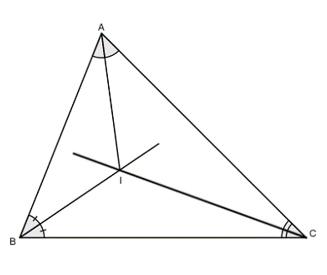
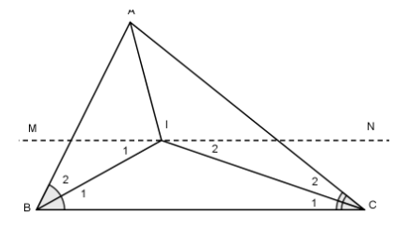
Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Tam giác ABC có ba đường phân giác giao nhau tại I, khi đó:
3. Ví dụ
Ví dụ 1:Tam giác ABC có trung tuyến AM đồng thời là phân giác. Chứng minh tam giác đó là tam giác cân
Hướng dẫn giải:
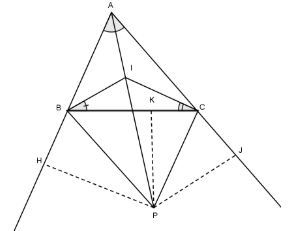
Ví dụ 2:Cho tam giác ABC có hai đường phân giác trong của hai góc B và góc C cắt nhau tại I và hai đường phân giác ngoài của hai góc ấy cắt nhau tại P. Chứng minh rằng A, I, P thẳng hàng
Hướng dẫn giải:
Hai phân giác góc trong của góc B^ và góc C^ cắt nhau tại I
Suy ra I cũng phải thuộc phân giác của góc A^
(tính chất ba đường phân giác) (1)
Từ P hạ PH, PK, PJ vuông góc lần lượt với AB, BC, AC.
Ta có: PH = PK (do P thuộc phân giác góc ngoài của góc B^)
Tương tự: PK = PJ ⇒ PH = PJ
Điều này chứng tỏ P thuộc phân giác góc A (2)
Từ (1) và (2) vậy A, I, P thẳng hàng.
4. Bài tập vận dụng
Bài 1: Hai đường phân giác của góc B và góc C cắt nhau tại I. Chứng minh rằng
Hướng dẫn giải:
Bài 2: Cho ΔABC. Gọi I là giao điểm của hai tia phân giác góc A và góc B. Qua I kẻ đường thẳng song song với BC, cắt AB tại M, cắt AC tại N. Chứng minh rằng MN = BM + CN
Hướng dẫn giải:
Ba phân giác của một tam giác cùng đi qua một điểm nên CI là tia phân giác của góc C
B. Bài Tập
Câu 1: Điểm E nằm trên tia phân giác góc A của tam giác ABC ta có:
A. E nằm trên tia phân giác góc B
B. E cách đều hai cạnh AB, AC
C. E nằm trên tia phân giác góc C
D. EB = EC
Lời giải:
Điểm E nằm trên tia phân giác góc A của tam giác ABC thì E cách đều hai cạnh AB,AC
Đáp án cần chọn là: B
Câu 2: Điểm M cách đều hai cạnh AB, AC của tam giác ABC thì:
Lời giải:
Điểm M cách đều hai cạnh AB, AC của tam giác ABC thì điểm M nằm trên tia phân giác của 
Đáp án cần chọn là: A
Câu 3: Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó:
A. AI là trung tuyến kẻ từ A
B. AI là đường cao kẻ từ A
C. AI là trung trực cạnh BC
D. AI là phân giác của góc A
Lời giải:
Hai đường phân giác CD và BE cắt nhau tại I mà ba đường phân giác của một tam giác cùng đi qua một điểm nên AI là phân giác của góc A.
Đáp án cần chọn là: D
Câu 4: Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó:
A. I cách đều ba đỉnh của tam giác ABC
B. IC = ID = IB = IE
C. I là điểm cách đều ba cạnh của tam giác ABC
D. Cả A,B đều đúng
Câu 5: Em hãy chọn chọn câu đúng nhất
A. Ba tia phân giác của một tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác
B. Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác
C. Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy
D. Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Lời giải:
+ Trọng tâm là giao điểm của ba đường trung tuyến nên đáp án A sai. Loại đáp án A.
+ Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác là đúng. Chọn đáp án B.
+ Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy sai vì tính chất này không phải đúng với mọi tam giác. Loại đáp án C.
+ Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó sai vì giao điểm của ba đường phân giác của tam giác là tâm đường tròn nội tiếp tam giác đó. Loại đáp án D.
Đáp án cần chọn là: B
Câu 6: Em hãy điền cụm từ thích hợp vào chỗ trống:
"Ba đường phân giác của tam giác giao nhau tại 1 điểm. Điểm đó cách đều ... của tam giác đó"
A. Ba đỉnh
B. Ba cạnh
C. Hai đỉnh
D. Bốn đỉnh
Lời giải:
Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Đáp án cần chọn là: B
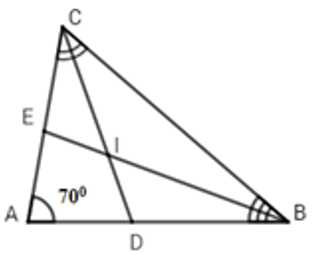
Câu 7: Cho ΔABC có Â = 70°, các đường phân giác BE và CD của 
Lời giải:
Xét ΔABC có: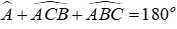 
(định lí tổng ba góc trong tam giác)
Vì CD là tia phân giác của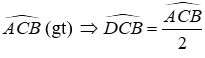 
(2) (tính chất tia phân giác )
Vì BE là tia phân giác của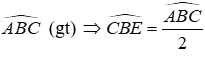 
(3) (tính chất tia phân giác )
Từ (1),(2),(3)
Xét ΔBIC có: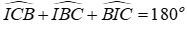 
(**) (định lí tổng ba góc trong tam giác)
Từ (*) và (**) 
Đáp án cần chọn là: A
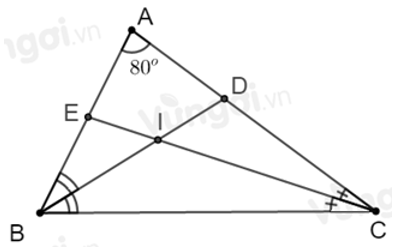
Câu 8: Cho ΔABC có Â = 80°, các đường phân giác BE và CD của 
Lời giải:
Xét ΔABC có: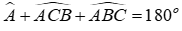 
(định lí tổng ba góc trong tam giác)
Vì CD là tia phân giác của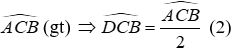 
(tính chất tia phân giác )
Vì BE là tia phân giác của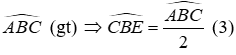 
(tính chất tia phân giác )
Xét ΔBIC có: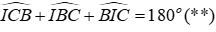 
(định lí tổng ba góc trong tam giác)
Từ (*) và (**) 
Đáp án cần chọn là: A
Câu 9: Cho ΔABC, các tia phân giác của góc B và A cắt nhau tại O. Qua O kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho BM = 2cm; CN = 3cm. Tính MN?
A. 5cm
B. 6cm
C. 7cm
D. 8cm
Lời giải:
Vì O là giao điểm của hai tia phân giác của các góc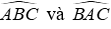 
(gt)
Suy ra, CO là tia phân giác của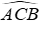 
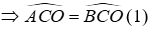
(tính chất 3 đường phân giác của tam giác)
(tính chất tia phân giác của một góc)
BO là tia phân giác của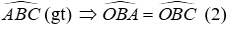 
(tính chất tia phân giác của một góc)
Vì MN//BC(gt)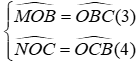 
(so le trong)
Từ (1) và (4)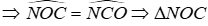 
cân tại N (dấu hiệu nhận biết tam giác cân)
⇒ NO = NC = 3cm (tính chất tam giác cân)
Từ (2) và (3)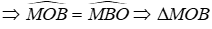 
cân tại M (dấu hiệu nhận biết tam giác cân)
⇒ MB = MO = 2cm (tính chất tam giác cân)
⇒ MN = MO + ON = 2 + 3 = 5cm
Đáp án cần chọn là: A
Câu 10: Cho ΔABC, các tia phân giác của góc B và A cắt nhau tại O. Qua O kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho BM = 3cm; CN = 4cm. Tính MN?
A. 7cm
B. 10cm
C. 11cm
D. 12cm
Lời giải:
Vì O là giao điểm của hai tia phân giác của các góc 
Suy ra, CO là tia phân giác của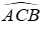 
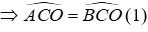
(tính chất 3 đường phân giác của tam giác)
(tính chất tia phân giác của một góc)
BO là tia phân giác của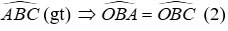 
(tính chất tia phân giác của một góc)
Vì MN//BC(gt)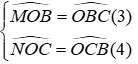 
(so le trong)
Từ (1) và (4)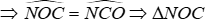 
cân tại N (dấu hiệu nhận biết tam giác cân)
⇒ NO = NC = 3cm (tính chất tam giác cân)
Từ (2) và (3)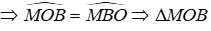 
cân tại M (dấu hiệu nhận biết tam giác cân)
⇒ MB = MO = 2cm (tính chất tam giác cân)
⇒ MN = MO + ON = 3 + 4 = 7cm
Đáp án cần chọn là: A
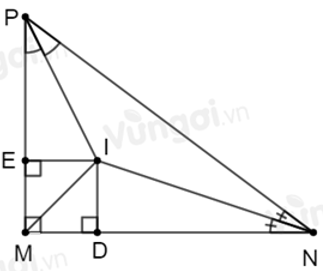
Câu 11: Cho ΔABC có Â = 90°, các tia phân giác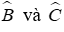 
cắt nhau tại I. Gọi D,E là chân các đường vuông góc hạ từ I đến các cạnh AB và AC. Khi đó ta có:
A. AI là đường cao của
B. IA = IB = IC
C. AI là đường trung tuyến của
D. ID = IE
Lời giải:
Xét ΔABC có các tia phân giác 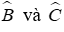cắt nhau tại I nên I là giao điểm của ba đường phân giác trong ΔABC, suy ra AI là đường phân giác của  và I cách đều ba cạnh của ΔABC (tính chất 3 đường phân giác của tam giác). Vậy ta loại đáp án A, B, C
Vì I là giao điểm của ba đường phân giác trong ΔABC nên DI = IE (tính chất 3 đường phân giác của tam giác).
Đáp án cần chọn là: D
Câu 12:Cho ΔMNP có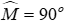 
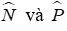
, các tia phân giác của 
cắt nhau tại I. Gọi D,E là chân các đường vuông góc hạ từ I đến các cạnh MN và MP. Tính IE biết ID = 4cm
Lời giải:
Xét ΔMNP có các tia phân giác của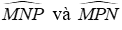 
cắt nhau tại I nên I là giao điểm của ba đường phân giác trong ΔMNP
Khi đó ID = IE (Tính chất ba đường phân giác của tam giác) mà ID = 4cm suy ra IE = 4cm
Đáp án cần chọn là: D
Câu 13: Cho ΔABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
A. I cách đều ba đỉnh của ΔABC
B. A,I,G thẳng hàng
C. G cách đều ba cạnh của ΔABC
D. Cả 3 đáp án trên đều đúng
Lời giải:
I là giao điểm của các đường phân giác trong tam giác nên I cách đều ba cạnh của ΔABC. Loại đáp án A
Ta có: ΔABC cân tại A, I là giao điểm của các đường phân giác trong tam giác nên AI vừa là đường trung tuyến đồng thời là đường phân giác của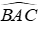 
. Mà G là trọng tâm của ΔABC nên A,G,I thẳng hàng. Chọn B
Đáp án cần chọn là: B
Câu 14: Cho ΔABC có I cách đều ba cạnh của tam giác. Gọi N là giao điểm của hai tia phân giác góc ngoài tại B và C. Khi đó ta có:
A. A, I, N thẳng hàng
B. I là giao điểm của ba đường trung tuyến của ΔABC
C. AN là đường phân giác của góc ngoài tại đỉnh A của ΔABC
D. Cả ba đáp án đều đúng
Lời giải:
Ta có: hai tia phân giác góc ngoài tại B và C của ΔABC cắt nhau tại N nên AN là tia phân giác của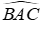 
(1)
ΔABC có: I cách đều ba cạnh của tam giác nên I là giao điểm của ba đường phân giác của ΔABC
Khi đó AI là tia phân giác của 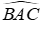(2)
Từ (1),(2) suy ra A, I, N thẳng hàng
Do đó A đúng, B, C, D sai
Đáp án cần chọn là: A
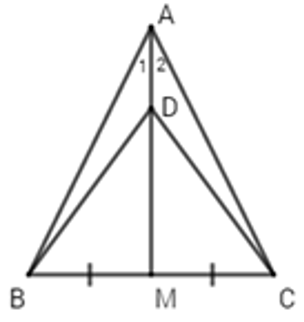
Câu 15: Cho ΔABC cân tại A, trung tuyến AM. Gọi D là một nằm giữa A và M. Khi đó ΔBDC là tam giác gì?
A. Tam giác cân
B. Tam giác đều
C. Tam giác vuông
D. Tam giác vuông cân
Lời giải:
Vì ΔABC cân tại A(gt) và AM là trung tuyến nên AM cũng là đường phân giác của 
⇒ BC = DC (2 cạnh tương ứng)
⇒ ΔBDC cân tại D (dấu hiệu nhận biết tam giác cân)
Đáp án cần chọn là: A
Câu 16: Cho ΔABC có trọng tâm G và I là giao của ba đường phân giác của tam giác ΔABC. Biết B; G; I thẳng hàng. Khi đó ΔABC là tam giác gì?
A. Tam giác cân tại B
B. Tam giác đều
C. Tam giác vuông
D. Tam giác vuông cân
Lời giải:
Vì I là giao của ba đường phân giác của tam giác ΔABC nên BI là đường phân giác của ΔABC
Vì G là trọng tâm ΔABC nên BG là đường trung tuyên của ΔABC mà B;I;G thẳng hàng
Do đó BI là đường trung tuyến của ΔABC
Xét ΔABC có: BI là đường trung tuyến đồng thời của ΔABC
Suy ra ΔABC cân tại B
Đáp án cần chọn là: A
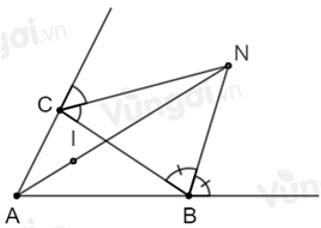
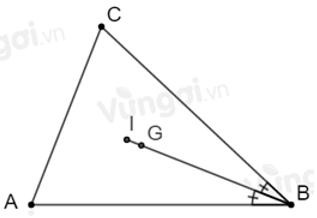
Câu 17:Cho tam giác ABC có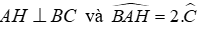 
. Tia phân giác của góc B cắt AC ở E. Tia phân giác của góc BAH cắt BE ở I. Khi đó tam giác AIE là tam giác gì?
A. Vuông cân tại I
B. Vuông cân tại E
C. Vuông cân tại A
D. Cân tại I
Lời giải:
Xét tam giác BEC có 
là góc ngoài tại đỉnh E nên
Xét tam giác AIB có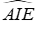 
là góc ngoài tại đỉnh I nên
Nên tam giác IAE vuông cân tại A
Đáp án cần chọn là: C
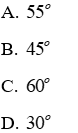
Câu 18: Cho tam giác ABC có Â = 120°. Các đường phân giác AD và BE. Tính số đo góc BED
Lời giải:
Gọi Ax là tia đối của tia AB.
Xét ΔABD có AE là tia phân giác của góc ngoài đỉnh A, BE là tia phân giác cả góc B và chúng cắt nhau tại E nên DE là tia phân giác góc ngoài của góc D
Mà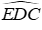 
là góc ngoài tại đỉnh D của tam giác BED nên
Đáp án cần chọn là: D
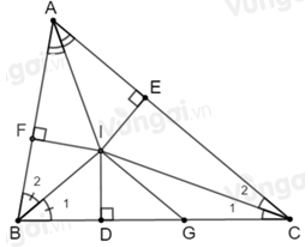
Câu 19: Cho tam giác ABC có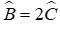 
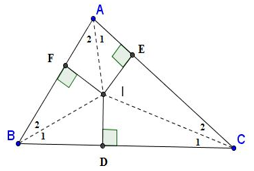
, các đường phân giác của góc B và C cắt nhau tại I. Chọn câu đúng
Lời giải:
Tam giác ABC có các đường phân giác của góc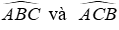 
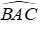
cắt nhau tại I nên AI là tia phân giác của 
(tính chất ba đường phân giác của tam giác)
Vì BI là tia phân giác của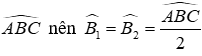 
(tính chất tia phân giác)
Xét ΔBFI vuông tại F và ΔBDI vuông tại D có:
Chứng minh tương tự ta có: AF = AE; CE = CD
Trên đoạn DC lấy điểm G sao cho: BD = DG
Xét ΔBDI vuông tại D và ΔGDI vuông tại D có:
Từ (1),(2) suy ra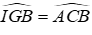 
mà hai góc này ở vị trí đồng vị nên IG//AC (dấu hiệu nhận biết hai đường thẳng song song)
Đáp án cần chọn là: A
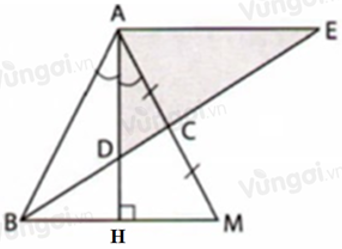
Câu 20: Cho tam giác ABC có AD thỏa mãn BD = 2DC. Trên tia đối tia CB lấy điểm E sao cho BC = CE. Khi đó tam giác ADE là tam giác
A. Cân tại A
B. Vuông tại D
C. Vuông tại A
D. Vuông tại E
Lời giải:
Kéo dài AC lấy điểm sao cho CM = AC, kéo dài AD cắt BM tại H
Vì AD là tia phân giác của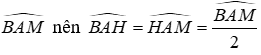 
(tính chất tia phân giác)
Xét ΔABM có: BC là đường trung tuyến ứng với cạnh AM, BD = 2DC (gt)
Do đó D là trọng tâm ΔABM
Suy ra AD là đường trung tuyến của ΔABM
Xét ΔABM có AD là đường trung tuyến đồng thời là đường phân giác
Do đó ΔABM cân tại A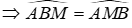 
(tính chất tam giác cân)
Trong ΔABM có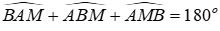 
(định lí tổng ba góc của tam giác)
Xét ΔABH có:
(định lí tổng ba góc của tam giác)
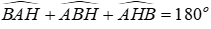
⇒ AE // BM (dấu hiệu nhận biết hai đường thẳng song song)
Mà AD ⊥ BM ⇒ AD ⊥ AE (quan hệ từ vuông góc tới song song)
Do đó ΔADE vuông tại A
Đáp án cần chọn là: C
