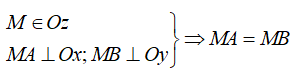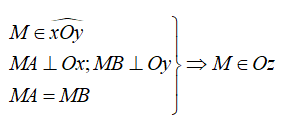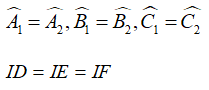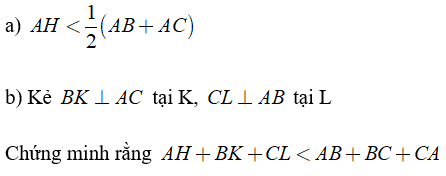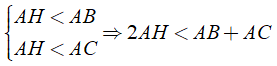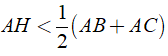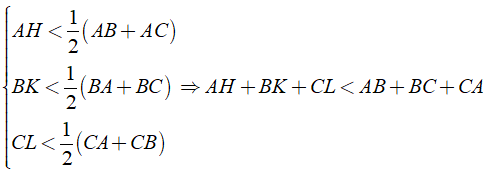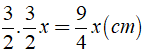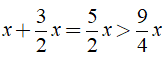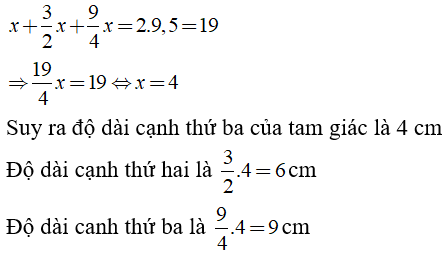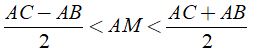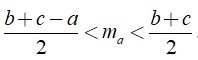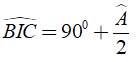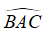Bài 60: Tổng hợp lý thuyết Chương 3 Hình học 7

A. Lý thuyết

1. Quan hệ giữa góc và cạnh đối diện

Góc đối diện với cạnh lớn hơn

Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

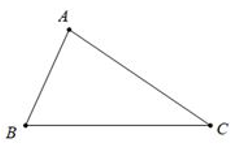
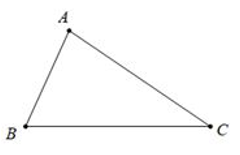
Ví dụ: ΔABC, AC > AB ⇒ ∠B > ∠C

Cạnh đối diện với góc lớn hơn

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Ví dụ: ΔABC, ∠B > ∠C ⇒ AC > AB

2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

Khái niệm đường thẳng vuông góc, đường xiên, hình chiếu của đường xiên

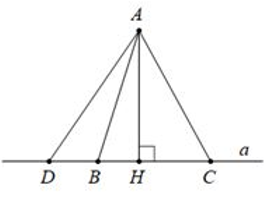
Từ điểm A không nằm trên đường thẳng d, kẻ một đường thẳng vuông góc với d tại H. Khi đó:

- Đoạn thẳng AH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d; điểm H gọi là chân của đường vuông góc hay hình chiếu của điểm A trên đường thẳng d.

- Đoạn thẳng AB gọi là một đường xiên kẻ từ điểm A đến đường thẳng d.

- Đoạn thẳng HB gọi là hình chiếu của đường xiên AB trên đường thẳng d.

Quan hệ giữa đường vuông góc và đường xiên

Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

Ví dụ: AH ⊥ a ⇒ AH < AC, AH < AD, AH < AB

Các đường xiên và hình chiếu của chúng

Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:

- Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

AH ⊥ a, HD > HC ⇒ AD > AC

- Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.

AH ⊥ a, AD > AC ⇒ HD > HC

- Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.

AB = AC ⇔ HB = HC

3. Quan hệ ba cạnh của tam giác và bất đẳng thức tam giác

Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.

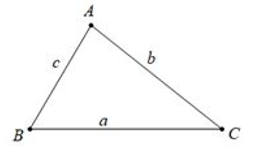
Cho tam giác ABC, ta có các bất đẳng thức sau:

      AB + AC > BC hay b + c > a

      AB + BC > AC hay c + a > b

      AC + BC > AB hay b + a > c

Hệ quả của bất đẳng thức tam giác

Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại.

Nhận xét: Nếu xét đồng thời cả tổng và hiệu độ dài hai cạnh của một tam giác thì quan hệ giữa các cạnh của nó còn được phát biểu như sau:

Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.

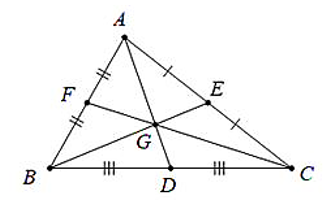
4. Tính chất đường trung tuyến của tam giác

- Định lý 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.

- Định lý 2: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

5. Tính chất đường phân giác của tam giác

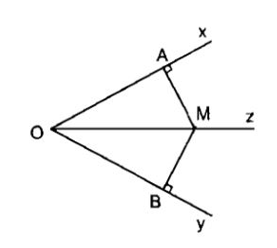
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó. (Định lý thuận).

Cho góc xOy có Oz là tia phân giác

Điểm nằm bên trong một góc và cách đều hai cạnh của góc đó thì nằm trên tia phân giác của góc đó.

Tính chất 3 đường phân giác

Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.

Tam giác ABC có ba đường phân giác giao nhau tại I, khi đó:

6. Tính chất của đường trung trực trong tam giác

Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó

Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

MA = MB ⇒ M thuộc đường trung trực của AB

Nhận xét: Từ hai định lý thuận và đảo, ta có: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

Tính chất: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.

Tính chất 3 đường trung trực trong tam giác

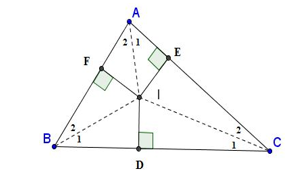
Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

Điểm O là giao điểm ba đường trung trực của tam giác ABC, ta có OA = OB = OC

Chú ý: Vì giao điểm O của ba đường trung trực của tam giác ABC cách đều ba đỉnh của tam giác đó nên có một đường tròn tâm O đi qua ba đỉnh A, B, C. Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác ABC.

7. Tính chất đường cao trong tam giác

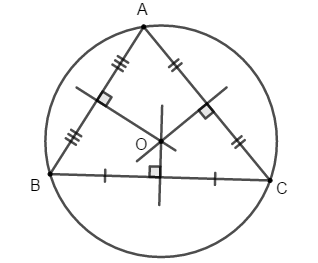
Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.

Tam giác ABC có H là giao điểm của ba đường cao. Khi đó H là trực tâm của tam giác ABC.

B. Bài tập

Bài 1: Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D nào đó khác điểm B và trên tia đối của tia CA người ta lấy điểm E sao cho CE = BD. Chứng minh BC nhỏ hơn DE.

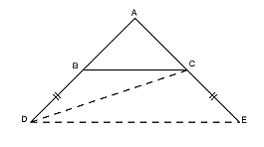
Xét ΔACD. Góc DCE là góc ngoài đỉnh C của tam giác ấy

Nên hai cạnh đối diện của hai góc đấy không bằng nhau.

Suy ra BC < DE

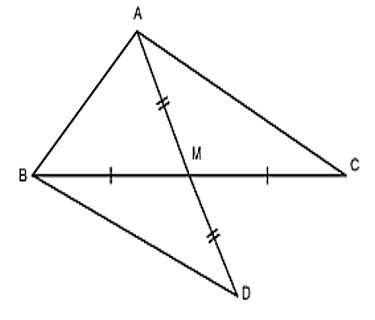
Bài 2: Cho ΔABC có AC > AB, M là trung điểm của BC. Nối AM, trên tia đối của MA lấy điểm D sao cho MA = MD. Nối BD. So sánh ∠BAM và ∠CAM

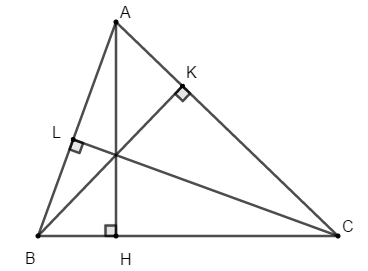
Bài 3: Cho ΔABC, kẻ AH ⊥ BC tại H, Chứng minh rằng:

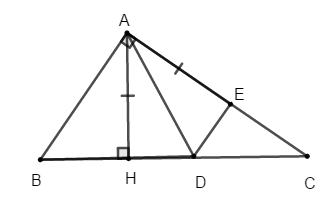
Bài 4: Cho tam giác ABC vuông tại A. Kẻ AH ⊥ BC . Trên cạnh huyền BC lấy điểm D sao cho BD = AB. Trên cạnh AC lấy điểm E sao cho AE = AH.

Chứng minh rằng DE ⊥ AC ⇒ BC + AH > AC + AB .

Bài 5: Hãy tìm độ dài các cạnh của một tam giác, biết cạnh thứ nhất gấp rưỡi cạnh thứ hai, cạnh thứ hai gấp rưỡi cạnh thứ ba và nửa chu vi tam giác bằng 9,5cm

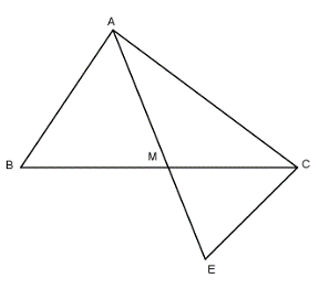
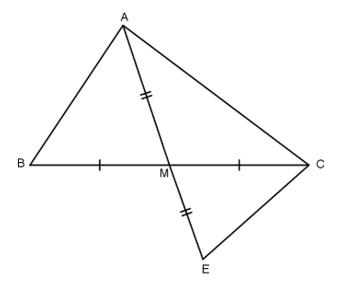
Bài 6: Cho tam giác ABC có AC > AB. Nối A với trung điểm M của BC. Trên tia AM lấy điểm E sao cho M là trung điểm của đoạn AE. Nối C với E.

a) So sánh hai đoạn thẳng AB và CE.

b) Chứng minh:

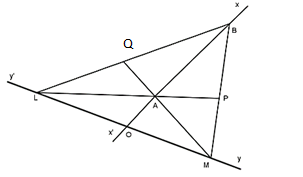
Bài 7: Cho hai đường thẳng xx' và yy' cắt nhau tại O. Trên tia Ox lấy hai điểm A, B sao cho A nằm giữa O và B, AB = 2OA. Trên yy' lấy hai điểm L và M sao cho O là trung điểm của LM. Nối B với L, B với M và gọi P là trung điểm của đoạn MB, Q là trung điểm của đoạn LB. Chứng minh rằng các đoạn thẳng LP và MQ đi qua A.

Bài 8: Cho ΔABC, BC = a, CA = b, AB = c. Kẻ trung tuyến AM. Đặt AM = m_a. Chứng minh rằng

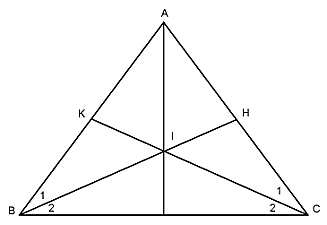
Bài 9: Cho tam giác ABC cân tại A. Từ B kẻ BH vuông góc với AC tại H và từ C kẻ CK vuông góc với AB tại K, hai đường thẳng BH và CK cắt nhau tại I. Chứng minh AI là đường phân giác của tam giác ABC.

Bài 10: Cho tam giác ABC vuông tại A. Dựng ở nửa mặt phẳng bờ BC, không chứa A, tam giác vuông cân CDB tại D. Chứng minh AD là tia phân giác của góc BAC

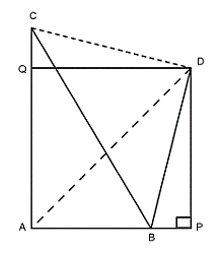
Điều đó chứng tỏ D nằm trên đường phân giác của góc BAC hay AD là đường phân giác của góc BAC.

Bài 11: Hai đường phân giác của góc B và góc C cắt nhau tại I. Chứng minh rằng

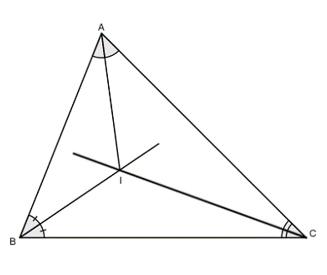
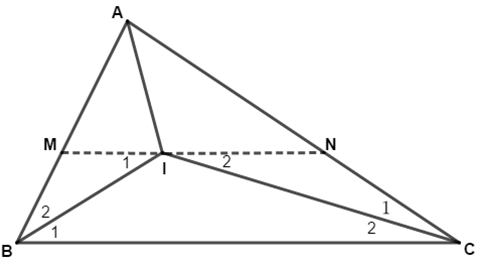
Bài 12: Cho ΔABC. Gọi I là giao điểm của hai tia phân giác góc A và góc B. Qua I kẻ đường thẳng song song với BC, cắt AB tại M, cắt AC tại N. Chứng minh rằng MN = BM + CN

Bài 13: Cho đoạn thẳng AB thuộc nửa mặt phẳng bờ d. Xác định điểm M thuộc d sao cho M cách đều hai điểm A, B.

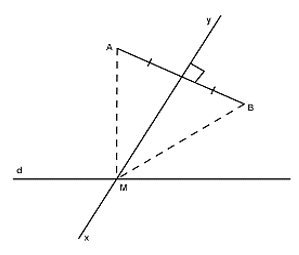
Vẽ trung trực xy của đoạn thẳng AB

Giả sử xy cắt d tại điểm M, ta có: MA = MB

   + Nếu AB ⊥ d thì xy // d, ta không xác định được điểm M

   + Ngoài trường hợp AB ⊥ d , ta luôn xác định được điểm M và M là duy nhất.

Bài 14: : Cho tam giác ABC có AC > AB, phân giác AD. Trên AC lấy điểm E sao cho AE = AB. Chứng minh rằng AD vuông góc với BE.

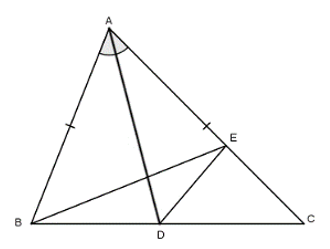
Nối BE và ED

Xét ΔADB và ΔADE có:

AD cạnh chung

∠BAD = ∠EAD (AD là tia phân giác góc BAC)

AB = AE (gt)

Do đó: ∠ADB = ∠ADE (c-g-c)

Suy ra DB = DE ⇒ D thuộc đường trung trực của đoạn BE

Lại có AB = AE (gt) ⇒ A thuộc đường trung trực của đoạn BE

Do đó AD là đường trung trực của BE

Hay AD vuông góc với BE

Bài 15: Cho tam giác ABC có đường phân giác AK của góc A. Biết rằng giao điểm của ba đường phân giác của tam giác ABK trùng với giao điểm ba đường trung trực của tam giác ABC. Tìm số đo các góc của tam giác ABC.

Hiển thị lời giải

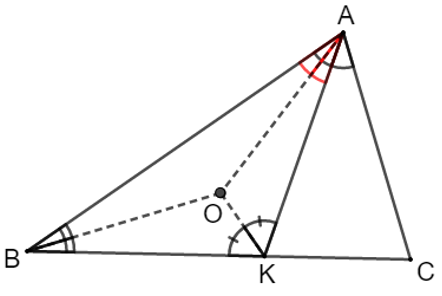
Gọi O là giao điểm của 3 đường phân giác của tam giác ABK

Theo đề bài, O là giao điểm của ba đường trung trực của tam giác ABC

Vậy OA = OB = OC

Do đó: các tam giác AOB, AOC, BOC đều là các tam giác cân tại đỉnh O

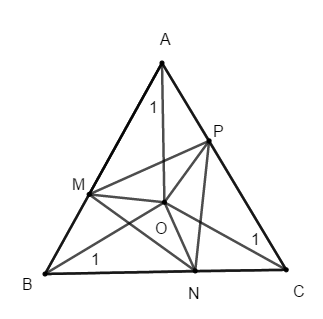
Bài 16: Trên ba cạnh AB, BC và CA của tam giác đều ABC, lấy các điểm theo thứ tự M, N, P sao cho AM = BN = CP. Gọi O là giao điểm của ba đường trung trực của tam giác ABC. Chứng minh O cũng là giao điểm của ba đường trung trực của tam giác MNP.

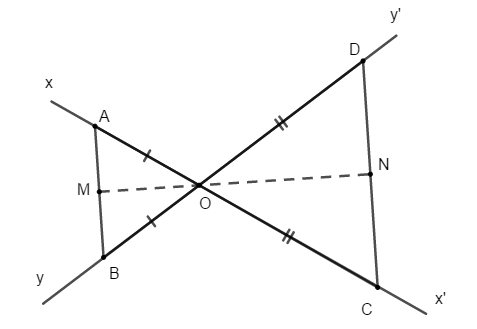
Bài 17: Cho hai đường thẳng xx' và yy' cắt nhau tại O. Trên Ox và Ox’ lần lượt lấy các điểm A và C; trên Oy và Oy’ lần lượt lấy các điểm B, D sao cho OA = OA, OC = OD. Gọi M, N lần lượt là trung điểm của AB, CD

Chứng minh M, O, N thẳng hàng.

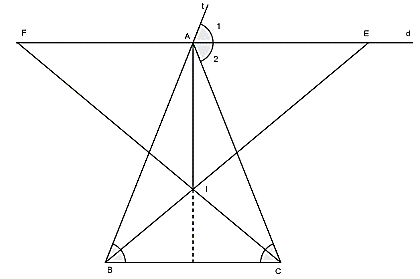
Bài 18:Cho tam giác ABC cân tại A. Qua A kẻ đường thẳng d song song với đáy BC. Các đường phân giác của góc B và góc C lần lượt cắt d tại E và F. Chứng minh rằng:

a) d là phân giác ngoài của góc A

b) AE = AF