Bài 59: Tính chất ba đường trung trực của tam giác 

A. Lý thuyết

1. Đường trung trực của tam giác

• Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.

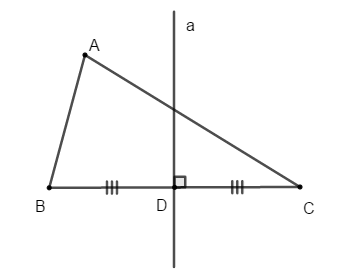
Ví dụ: a là đường trung trực ứng với cạnh BC của tam giác ABC.

• Mỗi tam giác có ba đường trung trực.

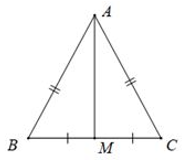
Tính chất: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.

Ta có: tam giác ABC cân tại A có đường trung trực của đoạn thẳng BC là AM, khi đó AM cũng là trung tuyến ứng với cạnh BC của tam giác ABC.

2. Tính chất ba đường trung trực của tam giác

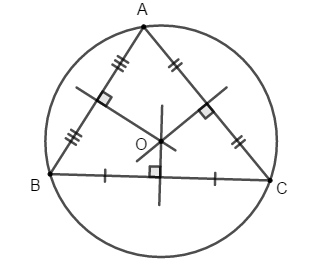
Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

Điểm O là giao điểm ba đường trung trực của tam giác ABC, ta có OA = OB = OC

Chú ý: Vì giao điểm O của ba đường trung trực của tam giác ABC cách đều ba đỉnh của tam giác đó nên có một đường tròn tâm O đi qua ba đỉnh A, B, C. Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác ABC.

3. Ví dụ

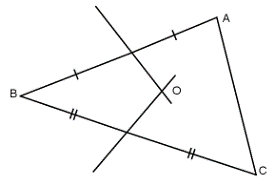
Ví dụ 1: Cho tam giác ABC. Tìm một điểm O cách đều ba điểm A, B, C

Hướng dẫn giải:

Điểm O cách đều hai điểm A, B suy ra điểm O nằm trên đường trung trực của AB

Điểm O cách đều hai điểm B, C suy ra điểm O nằm trên đường trung trực của BC

Điểm O cách đều hai điểm A, C suy ra điểm O nằm trên đường trung trực của AC

Do đó: điểm O cách đều ba điểm A, B, C thì O là giao điểm của ba đường trung trực của tam giác ABC.

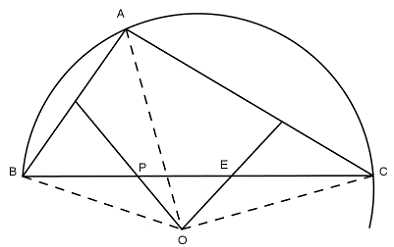
Ví dụ 2: Cho tam giác ABC có A^ là góc tù. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự tại P và E. Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ

Hướng dẫn giải:

Ta có O là điểm thuộc trung trực của đoạn AB nên OA = OB

Lại có O thuộc đường trung trực của đoạn AC nên OA = OC

Từ (1) và (2) suy ra OA = OB = OC

Vậy đường tròn (O, OA) đi qua các điểm A, B, C

B. Bài tập

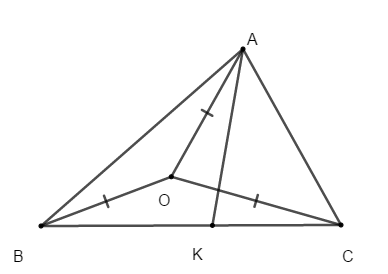
Bài 1: Cho tam giác ABC có đường phân giác AK của góc A. Biết rằng giao điểm của đường phân giác của tam giác ABK trùng với giao điểm ba đường trung trực của tam giác ABC. Tìm số đo các góc của tam giác ABC.

Hướng dẫn giải:

Gọi O là giao điểm của 3 đường phân giác của tam giác ABK

Theo đề bài, O là giao điểm của ba đường trung trực của tam giác ABC

Vậy OA = OB = OC

Do đó: các tam giác AOB, AOC, BOC là các tam giác cân tại đỉnh O

Khi đó:

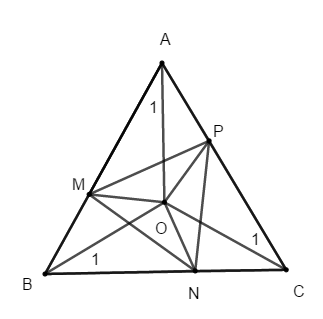
Bài 2: Trên ba cạnh AB, BC và CA của tam giác đều ABC, lấy các điểm theo thứ tự M, N, P sao cho AM = BN = CP. Gọi O là giao điểm của ba đường trung trực của tam giác ABC. Chứng minh O cũng là giao điểm của ba đường trung trực của tam giác MNP.

Hướng dẫn giải:

+ Theo giả thiết O là giao điểm của ba đường trung trực của tam giác ABC nên ta có: (giao điểm của ba đường trung trực trong tam giác cách đều ba đỉnh của tam giác)

+ Ta có: tam giác ABC đều có O là giao điểm ba đường trung trực nên O cũng là giao điểm của ba đường phân giác trong tam giác ABC

Suy ra AO, BO, CO lần lượt là các tia phân giác các góc BAC, ABC và ACB

Hay O là giao điểm của ba đường trung trực tam giác MNP.