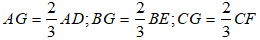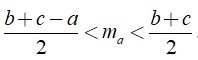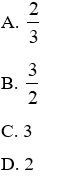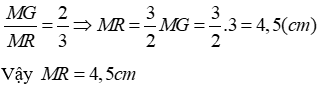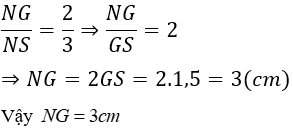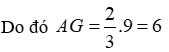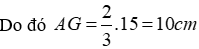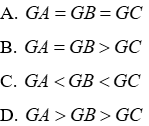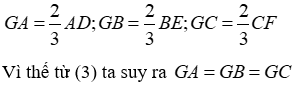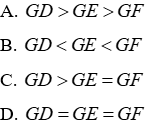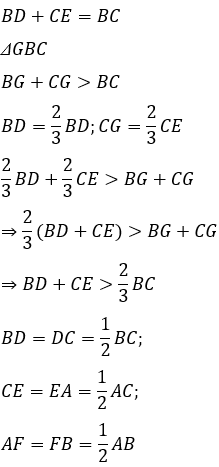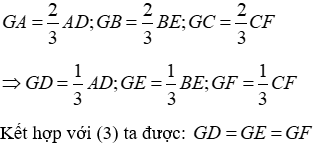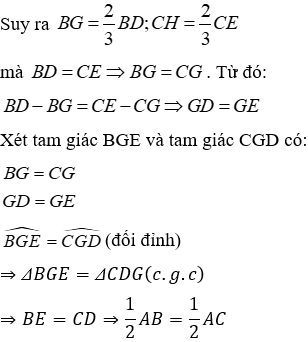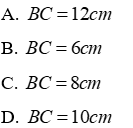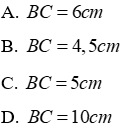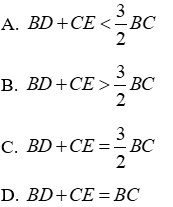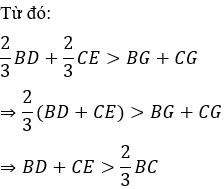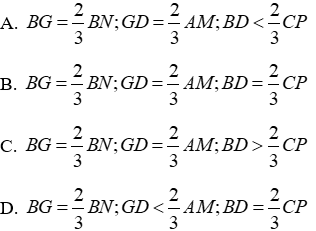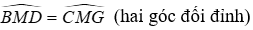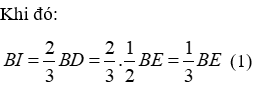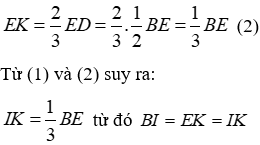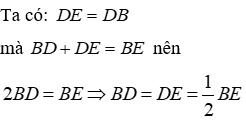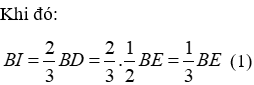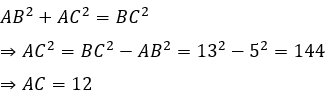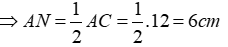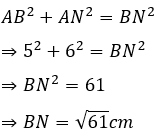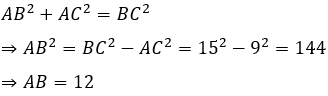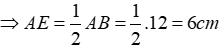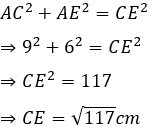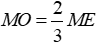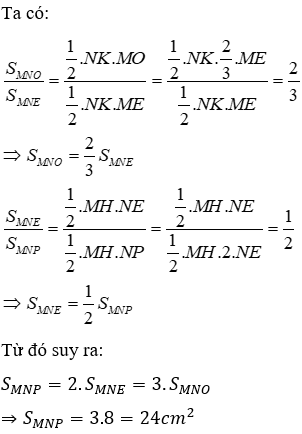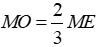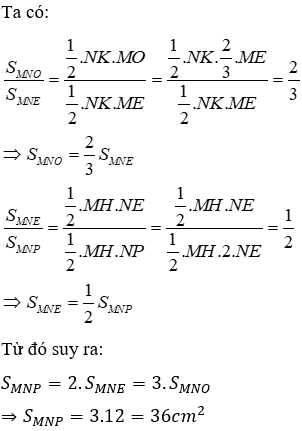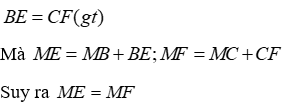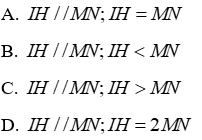Toán học 7 Bài 54: Tính chất ba đường trung tuyến của tam giác
Lý thuyết tổng hợp Toán học lớp 7 Bài 54: Tính chất ba đường trung tuyến của tam giác, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 54: Tính chất ba đường trung tuyến của tam giác
A. Lý thuyết
1. Đường trung tuyến của tam giác
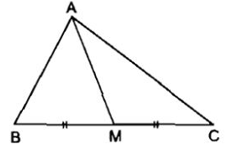
• Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC. Đôi khi, đường thẳng AM cũng gọi là đường trung tuyến của tam giác ABC.
• Mỗi tam giác có ba đường trung tuyến.
Đường trung tuyến của một tam giác là đoạn thẳng nối đỉnh và trung điểm cạnh đối diện
2. Tính chất ba đường trung tuyến của tam giác
• Định lý 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.
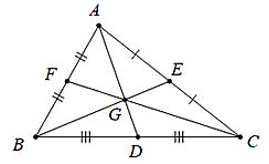
• Định lý 2: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Ví dụ: Với G là trọng tâm của ΔABC ta có:
3. Ví dụ
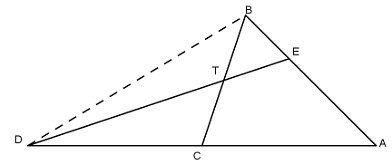
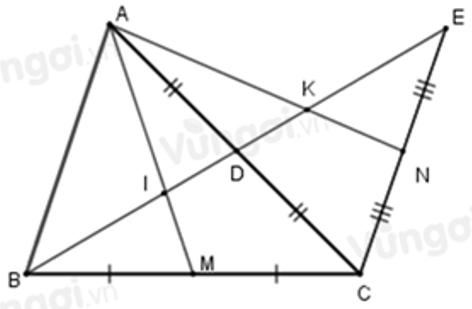
Ví dụ:Cho ΔABC, trên cạnh BC lấy điểm T sao cho TB = 2/3 BC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Đường thẳng DT cắt AB tại E. Chứng minh EA = EB
Hướng dẫn giải:
Trong ΔABD có: BC là trung tuyến vì CD = CA
Và TB = 2/3 BC, do đó T là trọng tâm của ΔABD
Suy ra DT là đường thẳng chứa trung tuyến xuất phát từ D
Nên phải qua trung điểm E của cạnh AB.
Vậy EA = EB
4. Bài tập vận dụng
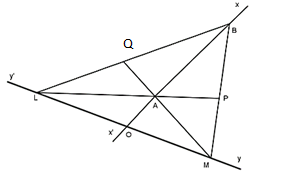
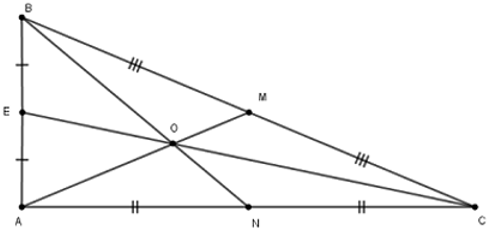
Bài 1: Cho hai đường thẳng xx' và yy' cắt nhau tại O. Trên tia Ox lấy hai điểm A, B sao cho A nằm giữa O và B, AB = 2OA. Trên yy' lấy hai điểm L và M sao cho O là trung điểm của LM. Nối B với L, B với M và gọi P là trung điểm của đoạn MB, Q là trung điểm của đoạn LB. Chứng minh rằng các đoạn thẳng LP và MQ đi qua A.
Hướng dẫn giải:
Ta có O là trung điểm của đoạn LM
Suy ra BO là đường trung tuyến của ΔBLM (1)
Mặt khác BO = BA + AO vì A nằm giữa O và B hay OB = 2OA + OA = 3OA
Suy ra AO = (1/3)OB hay BA = (2/3)BO (2)
Từ (1) (2) suy ra A là trọng tâm của ΔBLM (tính chất trọng tâm)
Mà LP và MQ là các đường trung tuyến của ΔBLM vì P là trung điểm MB và Q là trung điểm của đoạn LB
Suy ra các đoạn thẳng LP và MQ đi qua A (theo tính chất 3 đường trung tuyến)
Bài 2: Cho ΔABC, BC = a, CA = b, AB = c. Kẻ trung tuyến AM. Đặt AM = ma. Chứng minh rằng
Hướng dẫn giải:
B. Bài Tập
Câu 1: Chọn câu sai
A. Trong một tam giác có ba đường trung tuyến
B. Các đường trung tuyến của tam giác cắt nhau tại một điểm.
C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.
D. Một tam giác có hai trọng tâm
Lời giải:
+ Một tam giác chỉ có một trọng tâm nên đáp án D sai.
Đáp án cần chọn là: D
Câu 2: Chọn câu đúng
A. Trong một tam giác, đoạn thẳng nối từ đỉnh đến trung điểm cạnh đối diện là đường trung tuyến của tam giác.
B. Các đường trung tuyến của tam giác cắt nhau tại một điểm.
C. Trọng tâm của tam giác đó là giao của ba đường trung tuyến.
D. Cả A, B, C đều đúng.
Lời giải:
- Đường trung tuyến của tam giác là đoạn thẳng nối đỉnh của tam giác với trung điểm của cạnh đối diện nên A đúng.
- Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó nên B, C đúng.
Đáp án cần chọn là: D
Câu 3: Điền số thích hợp vào chỗ chấm: "Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng ... độ dài đường trung tuyến đi qua đỉnh ấy"
Lời giải:
Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng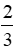 
độ dài đường trung tuyến đi qua đỉnh ấy.
Số cần điền là .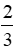
Đáp án cần chọn là: A
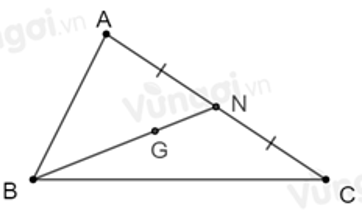
Câu 4: Cho tam giác ABC có G là trọng tâm tam giác, N là trung điểm AC. Khi đo BG = ... BN. Số thích hợp điền vào chỗ trống là:
Lời giải:
Đáp án cần chọn là: A
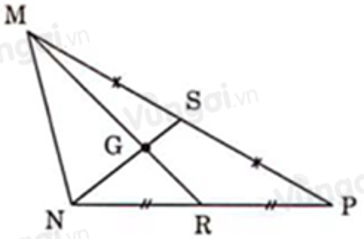
Câu 6: Cho hình vẽ sau
6.1: Biết MG = 3cm. Tính MR
A. 1 cm
B. 2 cm
C. 3 cm
D. 4,5 cm
Lời giải:
Ta có: MR, NS là hai đường trung tuyến của tam giác MNP và chúng cắt nhau tại G nên G là trọng tâm tam giác MNP
Theo tính chất ba đường trung tuyến của tam giác ta có:
Đáp án cần chọn là: D
>6.2: Biết GS = 1,5cm. Tính NG
A. 1,5 cm
B. 3 cm
C. 2,25 cm
D. 1 cm
Lời giải:
Theo câu trước ta có G là trọng tâm của tam giác MNP.
Theo tính chất ba đường trung tuyến của tam giác ta có:
Đáp án cần chọn là: B
Câu 7: Tam giác ABC có trung tuyến AM = 9cm và G là trọng tâm. Độ dài đoạn AG là
A. 4,5 cm
B. 3 cm
C. 6 cm
D. 4 cm
Lời giải:
Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên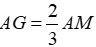 
(tính chất ba đường trung tuyến của tam giác)
Đáp án cần chọn là: C
Câu 8: Tam giác ABC có trung tuyến AM = 15cm và G là trọng tâm. Độ dài đoạn AG là
A. 7,5 cm
B. 5 cm
C. 10 cm
D. 22,5 cm
Lời giải:
Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên 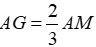(tính chất ba đường trung tuyến của tam giác)
Đáp án cần chọn là: C
Câu 9: Cho G là trọng tâm của tam giác đều. Chọn câu đúng
Lời giải:
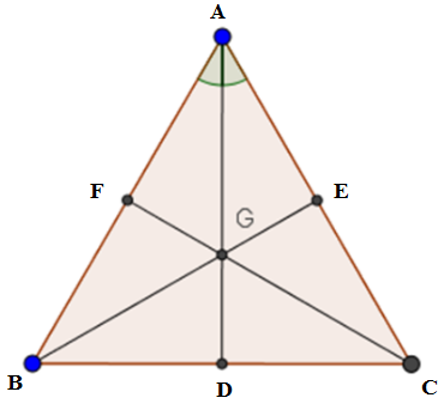
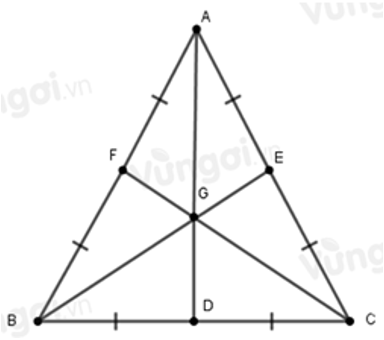
Các tia AG, BG và CG cắt BC,AC,AB lần lượt tại D,E,F thì D,E,F theo thứ tự lần lượt là trung điểm của BC,AC,AB
Mà AC=AB=BC (do tam giác ABC là tam giác đều), do đó
Theo đề bài G là trọng tâm của tam giác ABC nên ta có:
Đáp án cần chọn là: A
Câu 10: Cho G là trọng tâm của tam giác đều. D,E,F lần lượt là trung điểm của BC,AC,AB.Chọn câu đúng
Lời giải:
Vì D,E,F lần lượt là trung điểm của BC,AC,AB nên
Mặt khác AC=AB=BC (do tam giác ABC là tam giác đều), do đó
Chứng minh tương tự ta có ΔBEC = ΔADC(c.g.c) ⇒ BE = AD (2)
Từ (1) và (2) ta có: AD = BE = CF (3)
Theo đề bài G là trọng tâm của tam giác ABC nên ta có:
Đáp án cần chọn là: D
Câu 11: Cho tam giác ABC có hai đường trung tuyến BD; CE sao cho BD=CE. Khi đó tam giác ABC
A. Cân tại B
B. Cân tại C
C. Vuông tại A
D. Cân tại A
Lời giải:
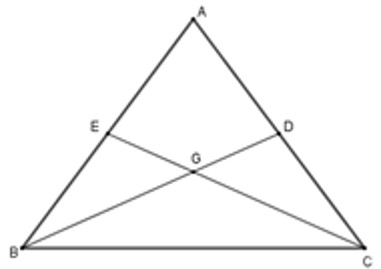
Hai đường trung tuyến BD và CE cắt nhau tại G suy ra G là trọng tâm tam giác ABC
Do đó AB = AC hay tam giác ABC cân tại A
Đáp án cần chọn là: D
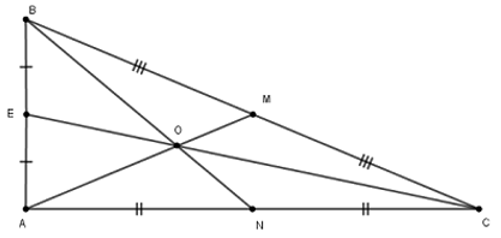
Câu 12: Cho tam giác ABC có hai đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài cạnh BC biết BD = 9cm; CE = 12cm
Câu 13: Cho tam giác ABC có hai đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài cạnh BC biết BD = 4,5cm; CE = 6cm
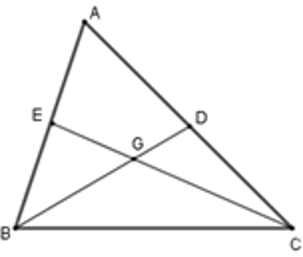
Câu 14: tam giác ABC, các đường trung tuyến BD và CE. Chọn câu đúng
Lời giải:
Gọi G là giao điểm của BD và CE. Trong ΔGBC ta có BG + CG > BC
Ta lại có: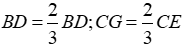 
(tính chất các đường trung tuyến của tam giác ABC)
Từ đó:
Đáp án cần chọn là: B
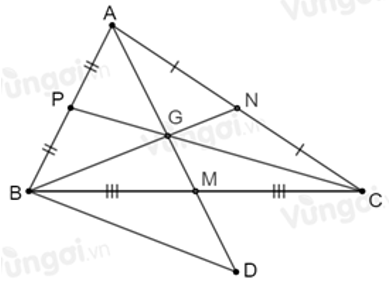
Câu 15: Cho tam giác ABC, có G là trọng tâm và các đường trung tuyến AM,BN,CP. Trên tia AG kéo dài lấy điểm D sao cho G là trung điểm của AD. So sánh các cạnh của tam giác BGD với các đường trung tuyến của tam giác ABC
Lời giải:
ΔABC có G là trọng tâm và các đường trung tuyến AM, BN, CP nên theo tính chất ba đường trung tuyến của tam giác ta có:
Ta có: GD = AG = 2GM (tính chất ba đường trung tuyến của tam giác)
Mà GD = GM + MD ⇒ 2GM = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG có:
GM = MD
BM = MC (vì AM là đường trung tuyến của ΔABC)
⇒ ΔBMD = ΔCMG (c.g.c)
Đáp án cần chọn là: B
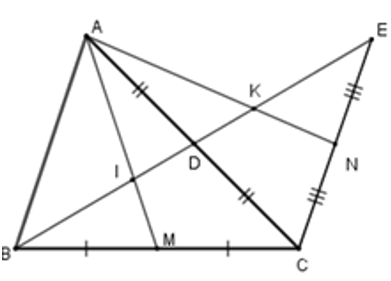
Câu 16: Cho tam giác ABC, đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = DB. Gọi M, N theo thứ tự là trung điểm của BC;CE. Gọi I;K theo thứ tự là giao điểm của AM,AN và BE. Chọn câu đúng
Lời giải:
Vì AM, DB là hai đường trung tuyến của tam giác ABC và chúng cắt nhau tại I nên I là trọng tâm tam giác ABC
Vì AN, ED là hai đường trung tuyến của tam giác ACE và chúng cắt nhau tại K nên K là trọng tâm tam giác ACE nên
Đáp án cần chọn là: C
Câu 17: Cho tam giác ABC, đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = DB. Gọi M, N theo thứ tự là trung điểm của BC;CE. Gọi I;K theo thứ tự là giao điểm của AM,AN và BE. Tính BE biết IK = 3cm
A. 6cm
B. 9cm
C. 12cm
D. 15cm
Lời giải:
Vì AM, DB là hai đường trung tuyến của tam giác ABC và chúng cắt nhau tại I nên I là trọng tâm tam giác ABC
Vì AN, ED là hai đường trung tuyến của tam giác ACE và chúng cắt nhau tại K nên K là trọng tâm tam giác ACE nên
Đáp án cần chọn là: B
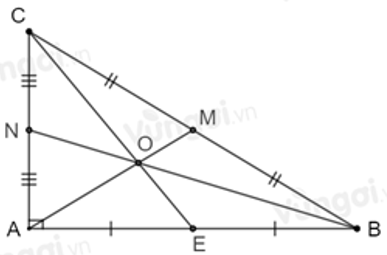
Câu 18:Cho tam giác ABC vuông tại A có: AB = 5cm; BC = 13cm. Ba đường trung tuyến AM, BN, CE cắt nhau tại O
Độ dài trung tuyến BN là:
Lời giải:
ΔABC vuông tại A nên theo định lí Pytago ta có:
Ta có AM, BN, CE là các đường trung tuyến ứng với các cạnh BC, AC, AB của tam giác vuông ABC
Suy ra M, N, E lần lượt là trung điểm của các cạnh BC, AC, AB
Áp dụng định lí Pytago vào tam giác ABN vuông tại A ta có:
Đáp án cần chọn là: B
Câu 19: Cho tam giác ABC vuông tại A có AC = 9cm, BC = 15cm. Ba đường trung tuyến AM, BN, CE cắt nhau tại O. Độ dài trung tuyến CE là
Lời giải:
ΔABC vuông tại A nên theo định lí Pytago ta có:
Ta có AM, BN, CE là các đường trung tuyến ứng với các cạnh BC, AC, AB của tam giác vuông ABC
Suy ra M, N, E lần lượt là trung điểm của các cạnh BC, AC, AB
Áp dụng định lí Pytago vào tam giác ACE vuông tại A ta có:
Đáp án cần chọn là: B
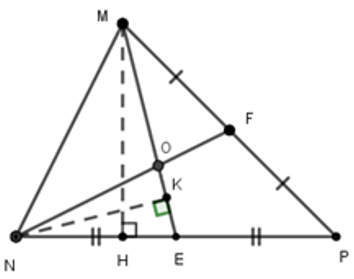
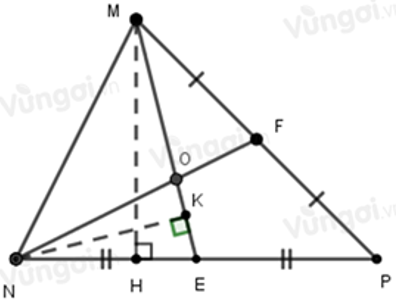
Câu 20: Cho tam giác MNP, hai đường trung tuyến ME,NF cắt nhau tại O. Tính diện tích tam giác MNP, biết diện tích tam giác MNO là 8 cm2
Lời giải:
Gọi MH là đường cao kẻ từ M xuống cạnh BC, NK là đường cao kẻ từ N xuống cạnh ME
Hai đường trung tuyến ME và NF cắt nhau tại O nên O là trọng tâm tam giác MNP, do đó
Có ME là trung tuyến ứng với cạnh NP nên E là trung điểm của NP, suy ra NP = 2NE
Đáp án cần chọn là: D
Câu 21: Cho tam giác MNP, hai đường trung tuyến ME,NF cắt nhau tại O. Tính diện tích tam giác MNP, biết diện tích tam giác MNO là 12 cm2
A. 18 cm2
B. 72 cm2
C. 54 cm2
D. 36 cm2
Lời giải:
Gọi MH là đường cao kẻ từ M xuống cạnh BC, NK là đường cao kẻ từ N xuống cạnh ME
Hai đường trung tuyến ME và NF cắt nhau tại O nên O là trọng tâm tam giác MNP, do đó
Có ME là trung tuyến ứng với cạnh NP nên E là trung điểm của NP, suy ra NP = 2NE
Đáp án cần chọn là: D
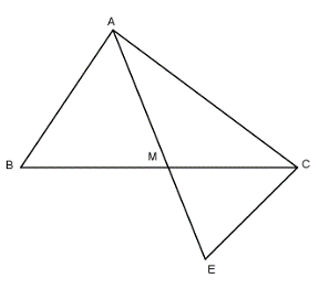
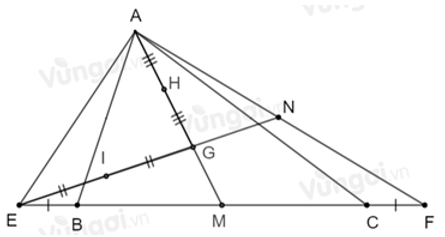
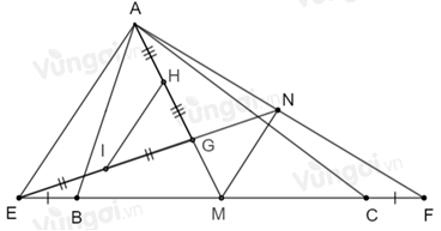
Câu 22: Cho ΔABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF. Gọi G là trọng tâm tam giác ABC. AG cắt BC tại M. Lấy H là trung điểm AG. Nối EG cắt AF tại N. Lấy I là trung điểm EG
22.1: Chọn câu đúng
A. Hai tam giác ABC và AEF có cùng trọng tâm
B. Hai tam giác ABC và AEC có cùng trọng tâm
C. Hai tam giác ABC và ABF có cùng trọng tâm
D. Hai tam giác AEM và AMF có cùng trọng tâm
Lời giải:
Ta có: MB = MC (vì AM là đường trung tuyến ứng với cạnh BC của ΔABC);
Do đó AM là đường trung tuyến ứng với cạnh EF của ΔAEF
Mặt khác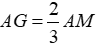 
(do G là trọng tâm ΔABC)
Vậy G là trọng tâm ΔAEF
Đáp án cần chọn là: A
22.2: Chọn câu đúng
Lời giải:
Theo câu trước ta có: G là trọng tâm ΔAEF nên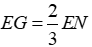 
(tính chất ba đường trung tuyến của tam giác)
Đáp án cần chọn là: A
Bài viết liên quan
- Toán học 7 Bài 52: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Toán học 7 Bài 53: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Toán học 7 Bài 55: Tính chất tia phân giác của một góc
- Toán học 7 Bài 56: Tính chất ba đường phân giác của tam giác
- Toán học 7 Bài 57: Tính chất đường trung trực của một đoạn thẳng
