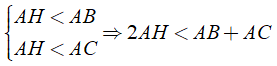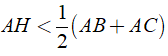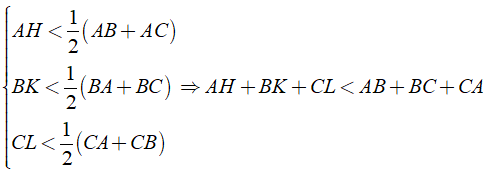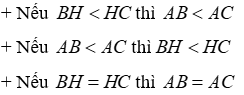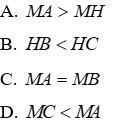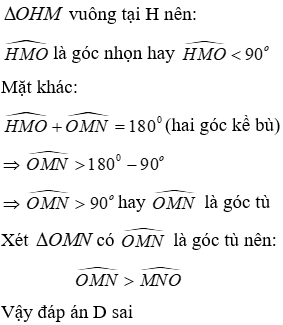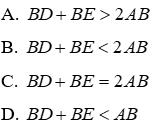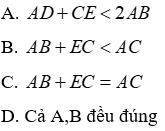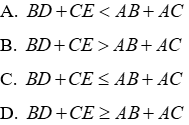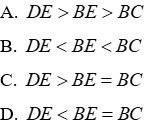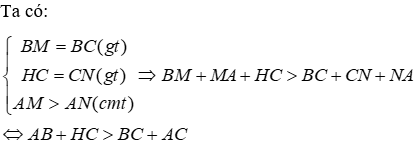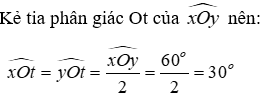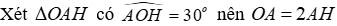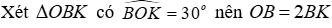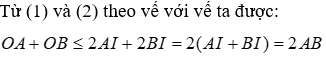Toán học 7 Bài 52: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Lý thuyết tổng hợp Toán học lớp 7 Bài 52: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 52: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
A. Lý thuyết
1. Khái niệm đường thẳng vuông góc, đường xiên, hình chiếu của đường xiên
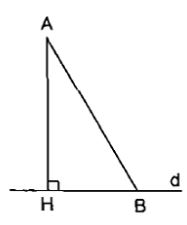
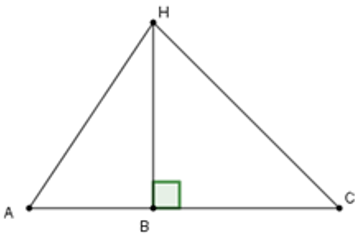
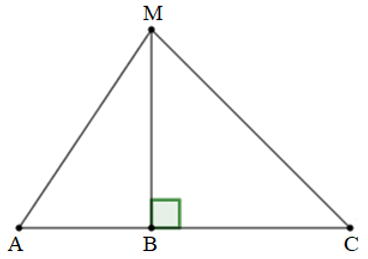
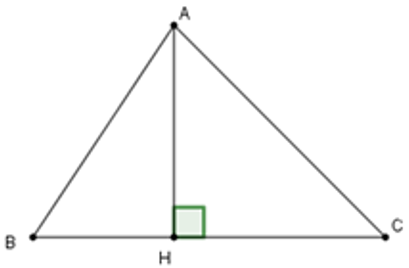
Từ điểm A không nằm trên đường thẳng d, kẻ một đường thẳng vuông góc với d tại H. Khi đó:
• Đoạn thẳng AH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d; điểm H gọi là chân của đường vuông góc hay hình chiếu của điểm A trên đường thẳng d.
• Đoạn thẳng AB gọi là một đường xiên kẻ từ điểm A đến đường thẳng d.
• Đoạn thẳng HB gọi là hình chiếu của đường xiên AB trên đường thẳng d.
2. Quan hệ giữa đường vuông góc và đường xiên
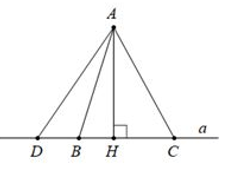
Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Ví dụ: AH ⊥ a ⇒ AH < AC, AH < AD, AH < AB
3. Các đường xiên và hình chiếu của chúng
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
• Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
AH ⊥ a, HD > HC ⇒ AD > AC
• Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
AH ⊥ a, AD > AC ⇒ HD > HC
• Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
AB = AC ⇔ HB = HC
4. Ví dụ
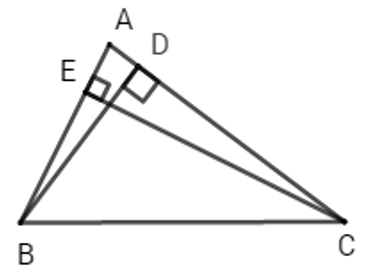
Ví dụ 1: Cho tam giác ABC vuông tại A. Lấy điểm B' trên cạnh AB, lấy điểm C' trên cạnh AC. So sánh B'C' với BC
Hướng dẫn giải:
Do B’ và C’ lần lượt nằm trên các cạnh AB và AC nên
Ta có: AC' < AC ⇒ B'C^' < B'C
(quan hệ giữa đường xiên và hình chiếu)
Lại có: AB' < AB ⇒ B'C < BC
(quan hệ giữa đường xiên và hình chiếu)
Khi đó ta có: B'C' < BC
Ví dụ 2:Cho tam giác ABC vuông tại A và tia phân giác CP. Chứng minh:
a) PA < CA
b) CP < CB
Hướng dẫn giải:
5. Bài tập vận dụng
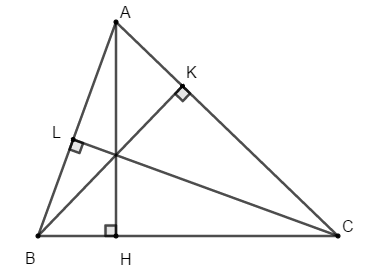
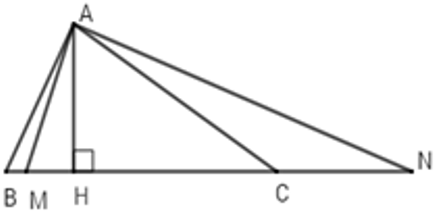
Bài 1: Cho ΔABC, kẻ AH ⊥ BC tại H, Chứng minh rằng:
Hướng dẫn giải:
a) Ta có:
AH là đường vuông góc
AB, AC là các đường xiên
Nên ta có: 
Hay 
b) Chứng minh tương tự như câu a), ta được BK, CL là đường cao hạ từ đỉnh B và C
Ta có: 
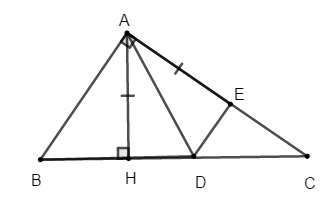
Bài 2: Cho tam giác ABC vuông tại A. Kẻ AH ⊥ BC . Trên cạnh huyền BC lấy điểm D sao cho BD = AB. Trên cạnh AC lấy điểm E sao cho AE = AH.
Chứng minh rằng DE ⊥ AC ⇒ BC + AH > AC + AB .
Hướng dẫn giải:
B. Bài Tập
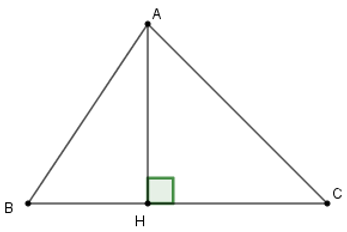
Câu 1: Em hãy chọn phát biểu sai trong các phát biểu sau:
A. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
B. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu lớn hơn thì lớn hơn
C. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn thì có hình chiếu nhỏ hơn
D. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau
Lời giải:
Trong các phát biểu ở ý A, B, và D đều đúng. Ý C sai vì: trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
Đáp án cần chọn là: C
Câu 2: Em hãy chọn cụm từ thích hợp điền vào chỗ trống:
"Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
A. lớn hơn
B. ngắn nhất
C. nhỏ hơn
D. bằng nhau
Lời giải:
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn.
Đáp án cần chọn là: C
Câu 3: Cho ba điểm a, b, c thẳng hàng và B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H. Khi đó:
Lời giải:
Vì BH là đường vuông góc và AH là đường xiên nên AH > BH
Đáp án cần chọn là: C
Câu 4: Cho ba điểm a, b, c thẳng hàng và B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm M. So sánh MB và MC, MB và MA
Lời giải:
Vì MB là đường vuông góc và MA, MC là đường xiên nên MA > MB, MC > MB (quan hệ giữa đường vuông góc và đường xiên)
Đáp án cần chọn là: C
Câu 5: Cho tam giác ABC có chiều cao AH
Lời giải:
Trong tam giác ABC có AH là đường vuông góc và BH; CH là hai hình chiếu
Khi đó:
Nên A, B, C đều đúng
Đáp án cần chọn là: D
Câu 6: Trong tam giác ABC có AH vuông góc với BC (H ∈ BC). Chọn câu sai
Lời giải:
Trong tam giác ABC có AH là đường vuông góc và BH; CH là hai hình chiếu
Khi đó:
Đáp án cần chọn là: B
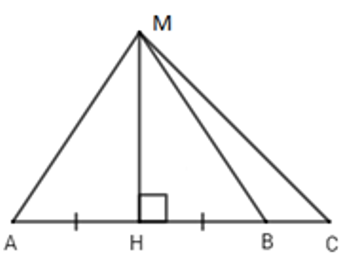
Câu 7: Cho hình vẽ sau:
Em hãy chọn đáp án sai trong các đáp án sau:
Lời giải:
Vì MH là đường vuông góc và MA là đường xiên MA > MH (quan hệ giữa đường vuông góc và đường xiên). Đáp án A đúng nên loại A
Xét ΔMBC có: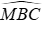 
là góc tù nên suy ra MB > MC (quan hệ giữa đường vuông góc và cạnh trong tam giác
Mà HB và HC lần lượt là hình chiếu của MB và MC trên AC
⇒ HB < HC (quan hệ giữa đường xiên và hình chiếu). Đáp án B đúng nên loại đáp án B
Vì AH = HB (gt) mà AH và HB lần lượt là hai hình chiếu của AM và BM
⇒ MA = MB (quan hệ giữa đường xiên và hình chiếu). Đáp án C đúng nên loại đáp án C
Ta có: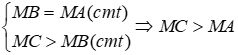 
. Đáp án D sai nên chọn đáp án D
Đáp án cần chọn là: D
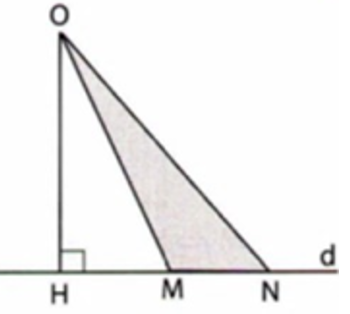
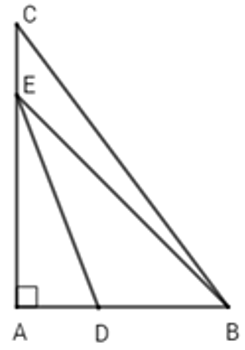
Câu 8: Cho hình vẽ sau:
Em hãy chọn khẳng định sai trong các khẳng định sau:
Lời giải:
Vì OH là đường vuông góc và OM,ON là đường xiên nên OH < OM; OH < ON (quan hệ giữa đường vuông góc và đường xiên)
Vì M nằm giữa hai điểm H và N nên HM < HN suy ra OM < ON (quan hệ giữa đường xiên và hình chiếu)
Đáp án cần chọn là: D
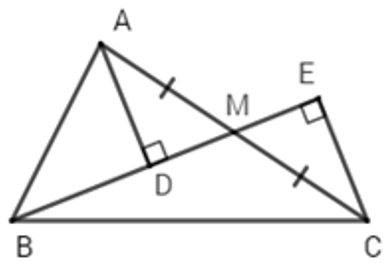
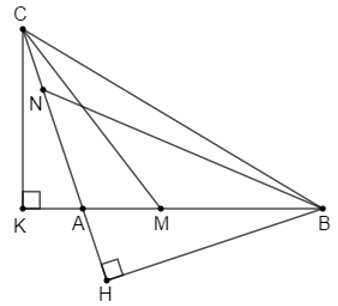
Câu 9: Cho ΔABC vuông tại A, M là trung điểm của AC. Gọi D,E lần lượt là hình chiếu A và C xuống đường thẳng BM. So sánh BD + BE và AB
Lời giải:
ΔABM vuông tại A (gt) nên BA < BM (quan hệ giữa đường vuông góc và đường xiên)
Mà BM = BD + DM ⇒ BA < BD + DM (1)
Mặt khác, BE = BE - ME ⇒ BA < BE - ME (2)
Cộng hai vế của (1) và (2) ta được: 2AB < BD + BE + MD - ME (3)
Vì M là trung điểm của AC(gt) ⇒AM=MC (tính chất trung điểm)
Xét tam giác vuông ADM và tam giác vuông CEM có
Đáp án cần chọn là: A
Câu 10: Cho ΔABC vuông tại A, M là trung điểm của AC, Gọi D, E lần lượt là hình chiếu A và C xuống đường thẳng BM. Chọn câu đúng nhất
Lời giải:
Vì M là trung điểm AC(gt) ⇒ AM = MC (tính chất trung điểm)
Xét tam giác ADM và tam giác CEM có:
⇒ 2AD < 2AB ⇒ AD + AD < 2AB hay AD + CE < 2AB (A đúng)
Đáp án cần chọn là: D
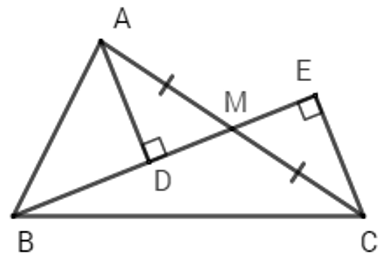
Câu 11: Cho ΔABC có CE và BD là đường cao. So sánh BD + CE và AB + AC?
Lời giải:
Vì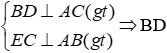 
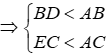
và CE lần lượt là hai đường vuông góc của hai đường xiên AC và AB
(đường vuông góc nhỏ hơn đường xiên)
⇒ BD + CE < AB + AC
Đáp án cần chọn là: A
Câu 12: Cho ΔABC có CE và BD là đường vuông góc (E ∈ AB, D ∈ AC). So sánh BD + CE và 2BC?
Lời giải:
Vì BD và BC lần lượt là đường vuông góc và đường xiên kẻ từ B đến AC nên BD < BC (1)
Vì CE và BC lần lượt là đường vuông góc và đường xiên kẻ từ C đến AB nên CE < BC (2)
Cộng (1) với (2) theo vế với vế ta được:
BD + CE < BC + BC hay BD + CE < 2BC
Đáp án cần chọn là: B
Câu 13: Cho ΔABC vuông tại A. Trên cạnh AB và AC lấy tương ứng hai điểm D và E (D, E không trùng với các đỉnh của ΔABC). Chọn đáp án đúng nhất
Lời giải:
Vì D nằm giữa A và B nên suy ra AD < AB. Mà AD và AB lần lượt là hình chiếu của ED và EB trên AB ⇒ ED < EB (1) (quan hệ giữa đường xiên và hình chiếu)
Vì E nằm giữa A và C nên suy ra AE < AC. Mà AE và AC lần lượt là hình chiếu của EB và BC trên AC ⇒ EB < BC (2) (quan hệ giữa đường xiên và hình chiếu)
Từ (1), (2) ⇒ ED < EB < BC
Đáp án cần chọn là: B
Câu 14: Cho ΔABC có 90° < Â < 180°. Trên cạnh AB và AC lấy tương ứng hai điểm M và N (M, N không trùng với các đỉnh của ΔABC). Chọn đáp án đúng nhất
Lời giải:
Từ B kẻ BH vuông góc với AC, vì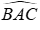 
là góc tù nên H nằm ngoài đoạn thẳng AC
Khi đó BA,BN,BC là đường xiên kẻ từ B đến AC,HA,HN,HC lần lượt là các hình chiếu của BA,BN,BC trên AC
Ta có: HA < HN < HC nên BA < BN < BC (quan hệ giữa đường xiên và hình chiếu)
Từ C kẻ CK vuông góc với AC, vì 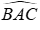là góc tù nên K nằm ngoài đoạn thẳng AB
Khi đó CA,CM,CB à các đường xiên kẻ từ C đém AB,AK,KM,KB lần lượt là các hình chiếu của CA,CM,CB trên AB
Ta có: KA < KM < KB nên CA < CM < CB (quan hệ giữa đường xiên và hình chiếu)
Chọn D
Đáp án cần chọn là: D
Câu 15: Cho D là một điểm nằm trong ΔABC. Nếu AD = AB thì:
Lời giải:
Gọi E là giao điểm BD và AC, kẻ AP ⊥ BD
Gọi AD = AB (gt) mà PD và BP lần lượt là hình chiếu của AB và AB trên BE
⇒ PD = BP (quan hệ giữa đường xiên và hình chiếu)
Do PE > PD = PB nên AE > AD (1). Mặt khác, AC > AE (2) nên từ (1) và (2) ⇒ AC > AB
Đáp án cần chọn là: C
Câu 16: Cho ΔABC có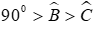 
. Kẻ AH ⊥ BC (H ∈ BC). Gọi M là một điểm nằm giữa H và B, N thuộc tia đối của tia CB
Lời giải:
Vì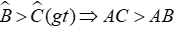 
(1) (quan hệ giữa góc và cạnh trong tam giác)
Mà HB, HC tương ứng hình chiếu của AB,AC trên BC
⇒ HB < HC (quan hệ giữa đường xiên và hình chiếu)
Đáp án cần chọn là: A
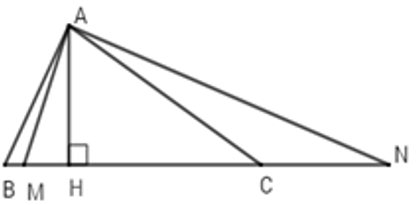
Lời giải:
Vì M nằm giữa B và H ⇒ HM < HB
Mà HM và HB tương ứng là hình chiếu của AM và AB trên BC
⇒ AM < AB (2) (quan hệ giữa đường xiên và hình chiếu)
Vì N thuộc tia đối của tia CB thì suy ra HN > HC. Mà HN và HC tương ứng là hình chiếu của AN và AC trên BC ⇒ AC < AN (3) (quan hệ giữa đường xiên và hình chiếu)
Từ (1),(2),(3) ⇒ AM < AB < AN
Đáp án cần chọn là: A
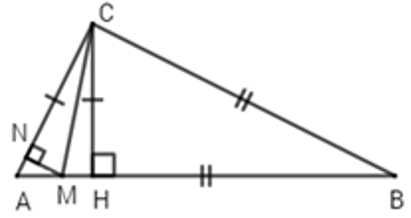
Câu 18: Cho ΔABC có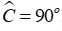 
, AC < BC, kẻ CH ⊥ AB. Trên các cạnh AB và AC lấy tương ứng hai điểm M và N sao cho BM = BC, CN = CH. Chọn câu đúng nhất
Lời giải:
Ta có: BM = BC (gt) ⇒ ΔBMC cân tại B (dấu hiệu nhận biết tam giác cân)
Xét ΔAMN có AN là đường vuông góc hạ từ A xuống MN và AM là đường xiên nên suy ra AM > AN (quan hệ đường vuông góc và đường xiên)
Đáp án cần chọn là: D
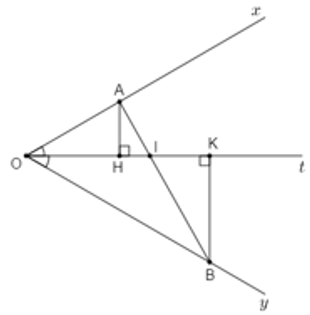
Câu 19: Cho góc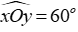 
, A là điểm trên tia Ox, B là điểm trên tia Oy (A,B không trùng với O)
Chọn câu đúng nhất
Lời giải:
Gọi I là giao của Ot và AB; H, K lần lần lượt là hình chiếu của A, B trên tia Ot
Vì AH, AI lần lượt là đường vuông góc, đường xiên kẻ từ A đến Ot nên AH ≤ AI do đó OA ≤ 2AI (1)
Vì BK, BI lần lượt là đường vuông góc, đường xiêm kẻ từ B đến Ot nên BK ≤ BI do đó OB ≤ 2BI
Dấu "=" xảy ra khi và chỉ lhi H, I, K trùng nhau hay AB ⊥ Ot nên:
Đáp án cần chọn là: D
Bài viết liên quan
- Toán học 7 Bài 50: Chương 4 Đại Số 7
- Toán học 7 Bài 51: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Toán học 7 Bài 53: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Toán học 7 Bài 54: Tính chất ba đường trung tuyến của tam giác
- Toán học 7 Bài 55: Tính chất tia phân giác của một góc
