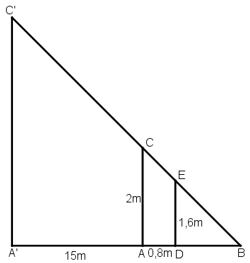
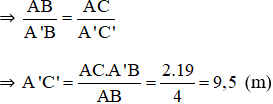Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người ấy lùi ra xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?
Quảng cáo
1 câu trả lời 478
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB 
Vậy cây cao 9,5m.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13107
Đã trả lời bởi chuyên gia
13107 -
 Đã trả lời bởi chuyên gia
12034
Đã trả lời bởi chuyên gia
12034 -
 Đã trả lời bởi chuyên gia
8837
Đã trả lời bởi chuyên gia
8837 -
 Đã trả lời bởi chuyên gia
6708
Đã trả lời bởi chuyên gia
6708 -
6006