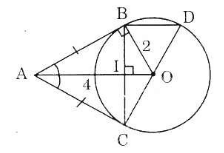
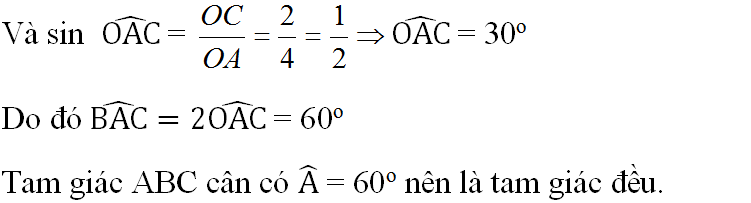Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của tam giác ABC; biết OB = 2cm, OA = 4cm.
Quảng cáo
1 câu trả lời 537
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
=> AC = √12 = 2√3 (cm)
Do đó AB = BC = AC = 2√3 (cm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13788
Đã trả lời bởi chuyên gia
13788 -
 Đã trả lời bởi chuyên gia
11080
Đã trả lời bởi chuyên gia
11080 -
 Đã trả lời bởi chuyên gia
10106
Đã trả lời bởi chuyên gia
10106 -
 Đã trả lời bởi chuyên gia
8367
Đã trả lời bởi chuyên gia
8367 -
6757
-
 Đã trả lời bởi chuyên gia
6006
Đã trả lời bởi chuyên gia
6006