Bài 6: Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F.
a. Chứng minh tam giác BEM = tam giác CFM.
b. Chứng minh AM là trung trực của EF.
c. Từ B kẻ đường thắng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đưong thắng này cắt nhau tại D. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Quảng cáo
1 câu trả lời 1594
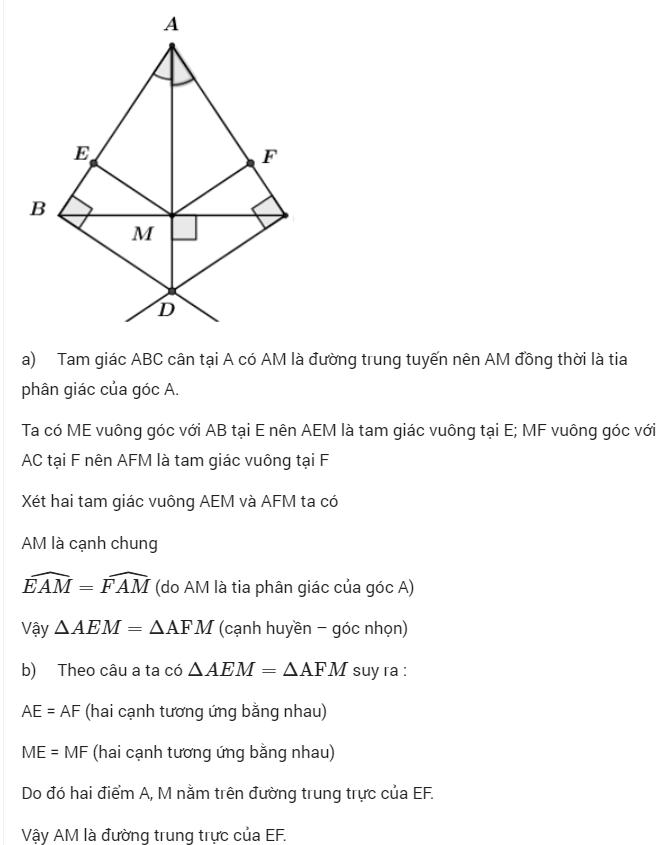
c) Xét hai tam giác vuông: ΔABD vuông tại B, ΔACD vuông tại C ta có:
AB = AC (do tam giác ABC cân tại A)
AD là cạnh chung
Vậy ΔABD=ΔACD (cạnh huyền – cạnh góc vuông)
Suy ra DB = DC (hai cạnh tương ứng bằng nhau)
Do đó D thuộc tia phân giác của góc A (1)
Lại có AM là tia phân giác của góc A, hay M thuộc tia phân giác của góc A (2)
Từ (1) và (2) suy ra 3 điểm A, M, D thẳng hàng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6566
Đã trả lời bởi chuyên gia
6566 -
 Đã trả lời bởi chuyên gia
5838
Đã trả lời bởi chuyên gia
5838 -
 Đã trả lời bởi chuyên gia
2542
Đã trả lời bởi chuyên gia
2542 -
 Đã trả lời bởi chuyên gia
2009
Đã trả lời bởi chuyên gia
2009 -
 Đã trả lời bởi chuyên gia
1510
Đã trả lời bởi chuyên gia
1510 -
 Đã trả lời bởi chuyên gia
1133
Đã trả lời bởi chuyên gia
1133


