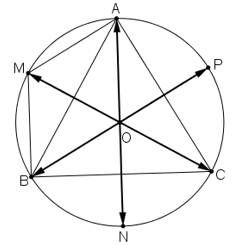
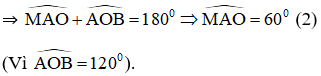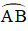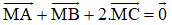Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:
Quảng cáo
1 câu trả lời 1596
a) 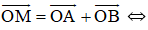
+ AOBM là hình bình hành ⇒ AM = OB
Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)
+ AOBM là hình bình hành ⇒ AM//BO
Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.
Mà 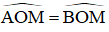
b) Chứng minh tương tự phần a) ta có: 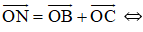
c) 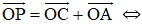
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
27792
Đã trả lời bởi chuyên gia
27792 -
 Đã trả lời bởi chuyên gia
22048
Đã trả lời bởi chuyên gia
22048 -
 Đã trả lời bởi chuyên gia
21596
Đã trả lời bởi chuyên gia
21596 -
 Đã trả lời bởi chuyên gia
12303
Đã trả lời bởi chuyên gia
12303 -
 Đã trả lời bởi chuyên gia
9565
Đã trả lời bởi chuyên gia
9565 -
 Đã trả lời bởi chuyên gia
9007
Đã trả lời bởi chuyên gia
9007
Gửi báo cáo thành công!