cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm (O) các đường cao AD BE CF cắt nhau tại H chứng minh rằng
4 điểm B,C,E,F cùng nằm trên một đường tròn
AE.AC=AH.AD;AD.BC=BE.AC
Quảng cáo
1 câu trả lời 1887
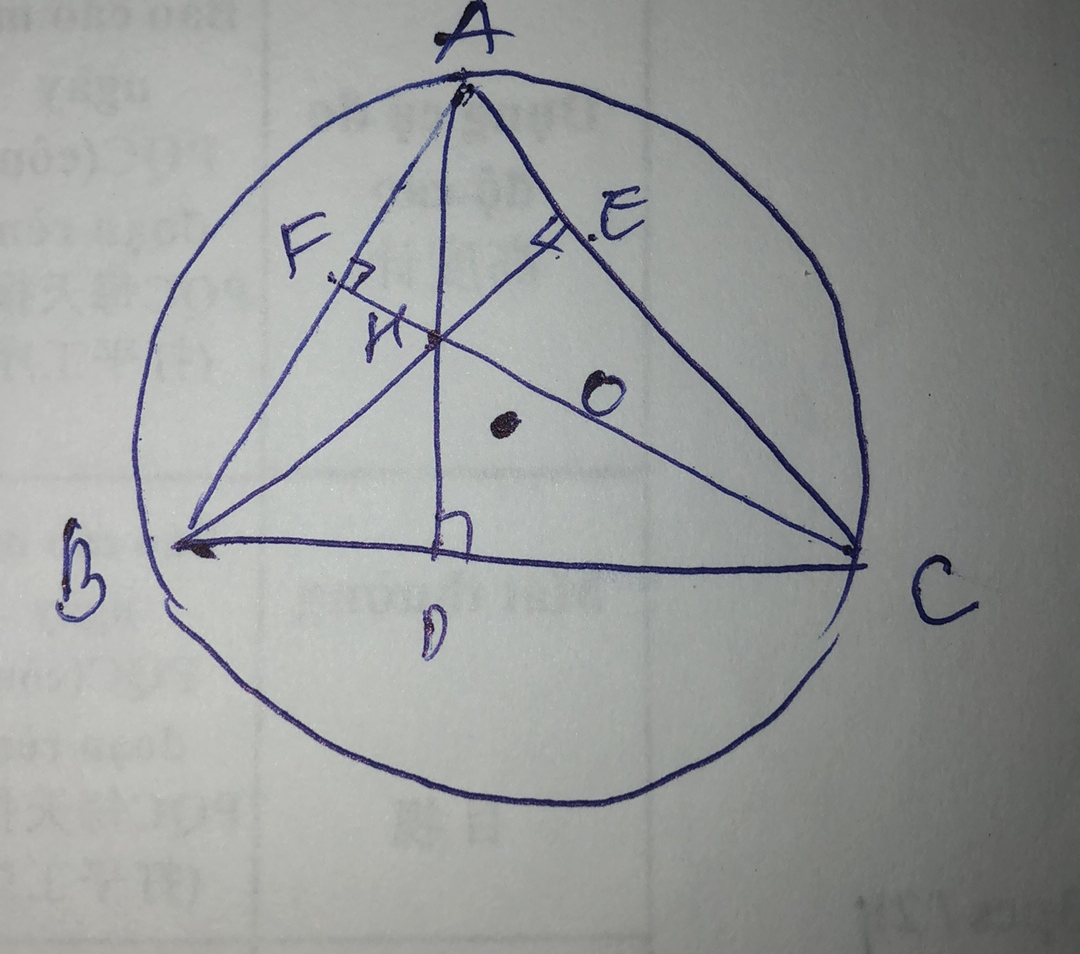
a) Vì BE,CF là hai đường cao của tam giác ABC
Nên: Góc BFC = Góc BEC = 90 độ
=> BFEC là tứ giác nội tiếp ( hai góc bằng nhau có đỉnh kề nhau cùng nhìn cạnh đối diện BC )
=> B,C,E,F cùng nằm trên một đường tròn ngoại tiếp tứ giác BFEC
b) Xét tam giác AEH và tam giác ADC
Ta có: Góc AEH = góc ADC = 90 độ
Góc DAC chung
=> Tam giác AEH và ADC đồng dạng ( g-g )
=> AE/AD=AH/AC => AE.AC = AH.AD ( Đpcm )
Lại có:
AD.BC=BE.AC=2 x SABC
=> Đpcm
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7447
Đã trả lời bởi chuyên gia
7447 -
 Đã trả lời bởi chuyên gia
5002
Đã trả lời bởi chuyên gia
5002 -
 Đã trả lời bởi chuyên gia
4658
Đã trả lời bởi chuyên gia
4658 -
 Đã trả lời bởi chuyên gia
4657
Đã trả lời bởi chuyên gia
4657 -
4446
Gửi báo cáo thành công!