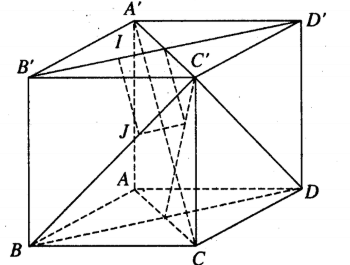
Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'.
Quảng cáo
1 câu trả lời 716
Gọi IJ là đường vuông góc chung của B'D' và BC', là vectơ pháp tuyến của mặt phẳng (P) qua B'D' và song song với AC', là vectơ pháp tuyến của mặt phẳng (Q) qua BC' và song song với A'C.
Khi đó = = (1; 1; 2)
= = (2; -1; 1)
Phương trình của (P) là: (x - 1) + y + 2(z - 1) = 0 hay x + y + 2z - 3 = 0.
Phương trình của (Q) là: 2(x - 1) - y + z = 0 hay 2x - y + z - 2 = 0.
Phương trình của (B'D') là: x = 1 - t, y = t, z = 1.
Phương trình của (BC') là: x = 1, y = t, z = t.
I là giao điểm của đường thẳng B'D' và (Q), để tìm tọa độ của I ta thế phương trình đường thẳng B'D' vào phương trình của (Q)
Ta có: 2(1 - t) - t + 1 - 2 = 0, hay t = 1/3. Từ đó suy ra I(2/3; 1/3; 1)
Tương tự, ta tìm được J(1; 2/3; 1/3).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
69541
Đã trả lời bởi chuyên gia
69541 -
 Đã trả lời bởi chuyên gia
67818
Đã trả lời bởi chuyên gia
67818 -
 Đã trả lời bởi chuyên gia
31042
Đã trả lời bởi chuyên gia
31042 -
 Đã trả lời bởi chuyên gia
Đã trả lời bởi chuyên gia
Trong không gian Oxyz, mặt cầu tâm I(-1;2;-3) và đi qua điểm A(2;0;0) có phương trình là:
A.
B.
C.
D.
28205 -
 Đã trả lời bởi chuyên gia
16276
Đã trả lời bởi chuyên gia
16276