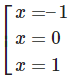Cho hàm số: y = f(x) = – 2m + –
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1.
b) Xác định m để đồ thị () của hàm số đã cho tiếp xúc với trục hoành tại hai điểm phân biệt.
Quảng cáo
1 câu trả lời 475
a) y = – 2
y′ = 4 – 4x = 4x( – 1)
y′ = 0 ⇔
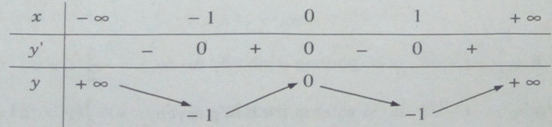
Bảng biến thiên:
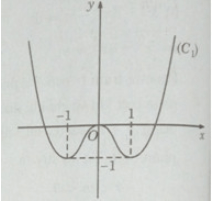
Đồ thị
b) y′ = 4 – 4mx = 4x( – m)
Để (Cm) tiếp xúc với trục hoành tại hai điểm phân biệt thì điều kiện cần và đủ là phương trình y’ = 0 có hai nghiệm phân biệt khác 0 và = 0.
+) Nếu m ≤ 0 thì – m ≥ 0 với mọi x nên đồ thị không thể tiếp xúc với trục Ox tại hai điểm phân biệt.
+) Nếu m > 0 thì y’ = 0 khi x = 0; x = hoặc x = -.
f(√m) = 0 ⇔ – 2 + – = 0 ⇔ (m – 2) = 0 ⇔ m = 2 (do m > 0)
Vậy m = 2 là giá trị cần tìm.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
40164
Đã trả lời bởi chuyên gia
40164 -
 Đã trả lời bởi chuyên gia
24713
Đã trả lời bởi chuyên gia
24713 -
 Đã trả lời bởi chuyên gia
24332
Đã trả lời bởi chuyên gia
24332 -
 Đã trả lời bởi chuyên gia
20971
Đã trả lời bởi chuyên gia
20971 -
 Đã trả lời bởi chuyên gia
20138
Đã trả lời bởi chuyên gia
20138 -
 Đã trả lời bởi chuyên gia
18186
Đã trả lời bởi chuyên gia
18186