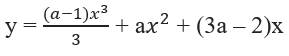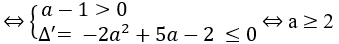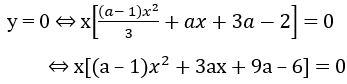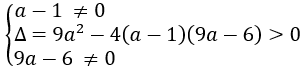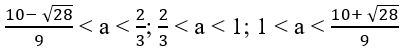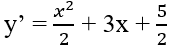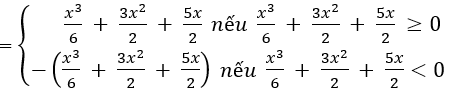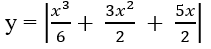Cho hàm số
a) Xác định a để hàm số luôn đồng biến.
b) Xác định a để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với a = 3/2.
Từ đó suy ra đồ thị của hàm số
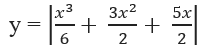
Quảng cáo
1 câu trả lời 343
a) Ta có
y' = (a - 1) + 2ax + 3a - 2.
Với a = 1, y' = 2x + 1 đổi dấu khi x đi qua -1/2. Hàm số không đồng biến.
Với a ≠ 1 thì với mọi x mà tại đó y' ≥ 0
(y' = 0 chỉ tại x = -2, khi a = 2).
Vậy với a ≥ 2 hàm số luôn đồng biến
b) Đồ thị cắt trục hoành tại ba điểm phân biệt khi và chỉ khi phương trình y = 0 có ba nghiệm phân biệt. Ta có
y = 0 có ba nghiệm phân biệt khi và chỉ khi phương trình
(a - 1) + 3ax + 9a - 6 = 0
Có hai nghiệm phân biệt khác 0. Muốn vậy, ta phải có
Giải hệ trên, ta được:
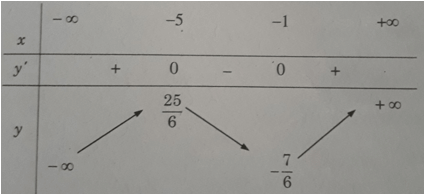
c) Khi a = 3/2 thì
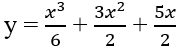
y' = 0 ⇔ + 6x + 5 = 0 ⇔ x = -1 hoặc x = -5.
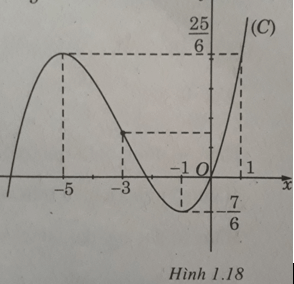
Đồ thị như trên Hình 1.18
Vì
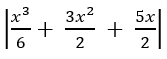
nên từ đồ thị (C) ta suy ngay ra đồ thị của hàm số
như trên Hình 1.19
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
40164
Đã trả lời bởi chuyên gia
40164 -
 Đã trả lời bởi chuyên gia
24713
Đã trả lời bởi chuyên gia
24713 -
 Đã trả lời bởi chuyên gia
24332
Đã trả lời bởi chuyên gia
24332 -
 Đã trả lời bởi chuyên gia
20971
Đã trả lời bởi chuyên gia
20971 -
 Đã trả lời bởi chuyên gia
20138
Đã trả lời bởi chuyên gia
20138 -
 Đã trả lời bởi chuyên gia
18186
Đã trả lời bởi chuyên gia
18186