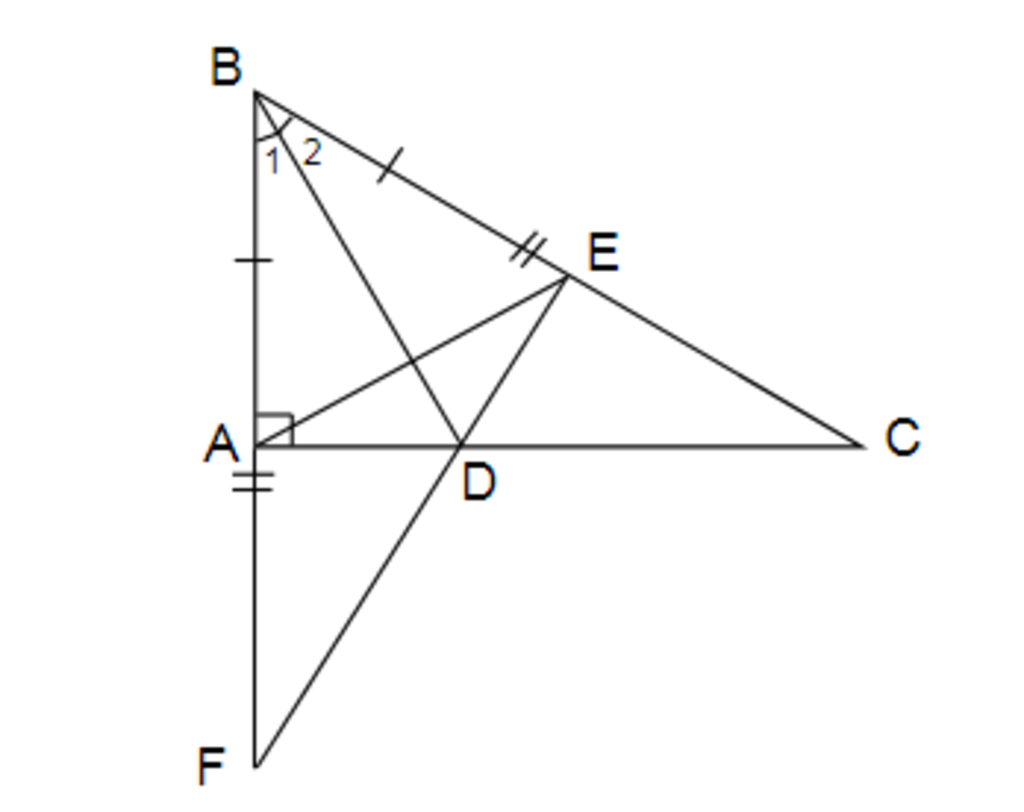
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA, trên tia BA lấy điểm F sao cho BF=BC. Kẻ BD là phân giác của ABC (D thuộc AC). Chứng minh rằng :
a, DE vuông góc BC
b, AD nhỏ hơn DC
c, Tam giác ADF= tam giác EDC E, F, D thẳng hàng vẽ hình và làm cho tôi
Quảng cáo
1 câu trả lời 46
a)Xét ΔABD và ΔEBD có:
AB = EB (gt)
ˆB1 = ˆB2 (theo gt)
BD: là cạnh chung
Vậy ΔABD = ΔEBD (c.g.c)
⇒ ˆBAD=ˆBED ( hai góc tương ứng)
Mà ˆBAD = 90 hay DE ⊥BC
Vì AB = EB (gt)
⇒ΔABE cân tại B
⇒ BD là đường phân giác đồng thời là đường trung trực của AE
Do AE ⊥ BD
b, Δ DEC vuông tại E
⇒ DE < EC (cạnh góc vuông bé hơn cạnh huyền)
Mà DA = DE
Do đó: DA < DC.
c) Xét hai tam giác vuông ADF và EDC có:
DA = DE
Do đó: DA < DC.
ˆADF =ˆEDC ⇒ ΔADF = ΔEDC
Ta có: Hai đường cao AC và EF cắt nhau tại D
⇒ D là trực tâm của tam giác
nên D ∈ EF
Do đó: ba điểm E, D, F thẳng hàng (đpcm).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8633
Đã trả lời bởi chuyên gia
8633 -
 Đã trả lời bởi chuyên gia
7630
Đã trả lời bởi chuyên gia
7630 -
6837
-
 Đã trả lời bởi chuyên gia
6546
Đã trả lời bởi chuyên gia
6546 -
 Đã trả lời bởi chuyên gia
6470
Đã trả lời bởi chuyên gia
6470 -
 Đã trả lời bởi chuyên gia
6326
Đã trả lời bởi chuyên gia
6326


