Bài 6: Cho tam giác ABC. O là giao của ba đường trung trực. Hai đường cao BE và CF giao nhau tại H. Gọi M là trung điểm BC. K là điểm nằm trên tia đối của tia OA sao cho OK=OA.
a) Chứng minh rằng: = = 90
b) Chứng minh rằng: BH // CK và CH // BK
c) Chứng minh rằng:AH = 2OM
Quảng cáo
3 câu trả lời 118
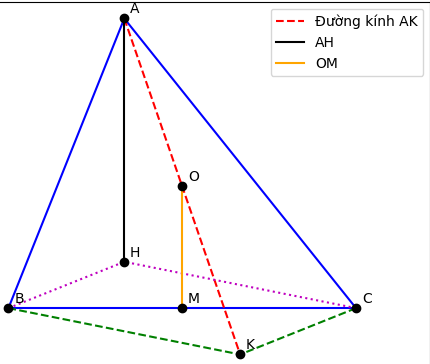
a) Chứng minh
- Ta có O là giao điểm ba đường trung trực của ABC, nên O là tâm đường tròn ngoại tiếp ABC.
=> OA = OB = OC = R.
- Theo giả thiết, K nằm trên tia đối của tia OA và OK = OA. Điều này có nghĩa là O là trung điểm của đoạn thẳng AK.
- Xét tam giác ABK:
+ O là trung điểm của AK (theo cách dựng).
+ OB = OA = OK = .
- Trong một tam giác, nếu đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.
Vậy: ABK vuông tại B => .
* Chứng minh tương tự với tam giác ACK:
OC = OA = OK = .
- Vậy ACK vuông tại C =>
b) Chứng minh BH // CK và CH // BK
* Chứng minh BH // CK:
- Ta có BE là đường cao nên BE AC, hay BH AC.
- Theo câu (a), .
- Vì BH và CK cùng vuông góc với AC nên BH // CK. (đpcm)
* Chứng minh CH // BK:
- Ta có CF là đường cao nên CF AB, hay CH AB.
- Theo câu (a), .
- Vì CH và BK cùng vuông góc với AB nên CH // BK. (đpcm)
c) Chứng minh AH = 2OM
- Xét tứ giác BHCK, vì là hình bình hành (chứng minh ở câu b), hai đường chéo cắt nhau tại trung điểm mỗi đường.
- Mà M là trung điểm của BC (giả thiết), nên M cũng phải là trung điểm của đường chéo còn lại là HK. Vậy H, M, K thẳng hàng và MH = MK.
- Xét tam giác AHK:
+ O là trung điểm của AK (cách dựng điểm K).
+ M là trung điểm của HK (chứng minh trên).
- Do đó, OM là đường trung bình của tam giác AHK.
=> Theo tính chất đường trung bình: (đpcm).
Gợi ý:
$\color{blue}{\text{Dưới đây là lời giải chi tiết cho bài toán hình học về các điểm đặc biệt trong tam giác:}}$
$\color{blue}{\text{a) Chứng minh: } \widehat{ABK} = \widehat{ACK} = 90^\circ}$
$\color{blue}{\text{Vì } O \text{ là giao điểm ba đường trung trực của } \triangle ABC \text{ nên } O \text{ là tâm đường tròn ngoại tiếp } \triangle ABC\text{.}}$
$\color{blue}{\text{Ta có } OA = OB = OC = R \text{ (bán kính).}}$
$\color{blue}{\text{Theo đề bài, } K \text{ nằm trên tia đối của tia } OA \text{ và } OK = OA \text{, do đó } AK \text{ là đường kính của đường tròn } (O)\text{.}}$
$\color{blue}{\text{Xét } \triangle ABK \text{ nội tiếp đường tròn } (O) \text{ có cạnh } AK \text{ là đường kính, nên } \triangle ABK \text{ vuông tại } B\text{.}}$
$\color{blue}{\text{Tương tự, } \triangle ACK \text{ nội tiếp đường tròn } (O) \text{ có cạnh } AK \text{ là đường kính, nên } \triangle ACK \text{ vuông tại } C\text{.}}$
$\color{blue}{\text{b) Chứng minh: } BH \parallel CK \text{ và } CH \parallel BK}$
$\color{blue}{\text{Ta có } CH \perp AB \text{ (vì } CF \text{ là đường cao) và } BK \perp AB \text{ (chứng minh ở câu a).}}$
$\color{blue}{\text{Ta có } BH \perp AC \text{ (vì } BE \text{ là đường cao) và } CK \perp AC \text{ (chứng minh ở câu a).}}$
$\color{blue}{\implies \text{Tứ giác } BHCK \text{ là hình bình hành.}}$
$\color{blue}{\text{c) Chứng minh: } AH = 2OM}$
$\color{blue}{\text{Vì } BHCK \text{ là hình bình hành (theo câu b), mà } M \text{ là trung điểm của đường chéo } BC\text{.}}$
$\color{blue}{\text{Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm mỗi đường, nên } M \text{ cũng là trung điểm của } HK\text{.}}$
$\color{blue}{\text{Xét } \triangle AHK\text{, ta có:}}$
$\color{blue}{O \text{ là trung điểm của } AK \text{ (do } AK \text{ là đường kính).}}$
$\color{blue}{M \text{ là trung điểm của } HK \text{ (chứng minh trên).}}$
$\color{blue}{\text{Suy ra } OM \text{ là đường trung bình của } \triangle AHK\text{.}}$
$\color{blue}{\text{Theo tính chất đường trung bình:}}$
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5957
Đã trả lời bởi chuyên gia
5957 -
 Đã trả lời bởi chuyên gia
4195
Đã trả lời bởi chuyên gia
4195


