LT1: Cho tam giác ABC có AB = AC và AB > BC. Gọi M là trung điểm của cạnh BC.
a) Chứng minh: AM vuông góc với BC.
b) Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh: DE // BC và MD = ME.
c) Trên tia đối của tia ME lấy điểm N sao cho ME = MN. Chứng minh: DN // AM.
LT2: Cho tam giác ABC vuông tại A có AB = AC. Gọi E là trung điểm của BC.
a) Chứng minh: AE vuông góc với BC.
b) Trên tia AE lấy điểm D sao cho AE = ED. Chứng minh: AC vuông góc với CD.
c) Gọi H là trung điểm của AC, trên tia EH lấy điểm K sao cho EH = HK. Chứng minh: AH là tia phân giác của góc EAK.
(ko sử dụng kiến thức tam giác cân nhé)
Quảng cáo
2 câu trả lời 107
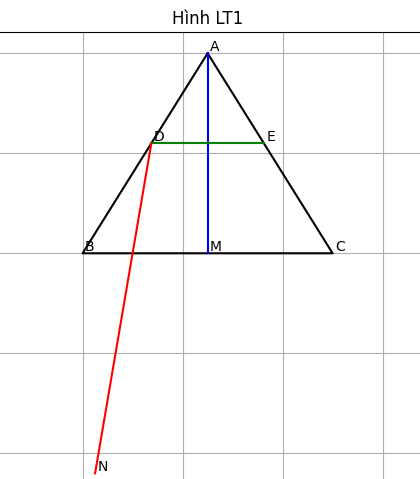
a) Chứng minh: AM ⊥ BC
- Vì M là trung điểm BC ⇒ MB = MC.
- Xét hai tam giác ABM và ACM, ta có:
AB = AC (giả thiết)
MB = MC (M trung điểm BC)
AM chung
⇒ ΔABM = ΔACM (c.g.c)
=> (tương ứng)
- Hai góc này là hai góc kề bù trên đường thẳng BC, mà lại bằng nhau, nên mỗi góc = 90∘.
⇒ AM ⟂ BC.
b) Chứng minh: DE // BC và MD = ME
- Trên AB lấy D, trên AC lấy E sao cho AD = AE
- Xét ΔADM và ΔAEM, ta có:
AD = AE (giả thiết)
AM chung
- Ta đã biết ở câu (a):
(vì AM là đường cao ⇒ AM là tia phân giác của )
- Trong ΔABM = ΔACM đã chứng minh, suy ra:
+ Mà D nằm trên AB, E nằm trên AC ⇒ .
- Do đó xét ΔADM và ΔAEM, ta có:
AM chung
AD = AE
⇒ ΔADM = ΔAEM (c.g.c)
=> MD = ME (tương ứng)
là góc ngoài tại M của hai tam giác bằng nhau nên DE // BC
(góc so le trong bằng nhau).
⇒ DE // BC và MD = ME.
c) Chứng minh: DN // AM
Trên tia đối của ME lấy N sao cho ME = MN.
Ta có MD = ME (câu b).
Lại có ME = MN (giả thiết).
⇒ MD = MN.
- Nằm trên tia đối của ME, nên M–E–N thẳng hàng.
- Xét tam giác DMN, ta có: MD = MN ⇒ tam giác DMN cân tại M
⇒
Mà là hai góc so le trong (N–M–E thẳng hàng).
Do bằng nhau ⇒ DN // AM.
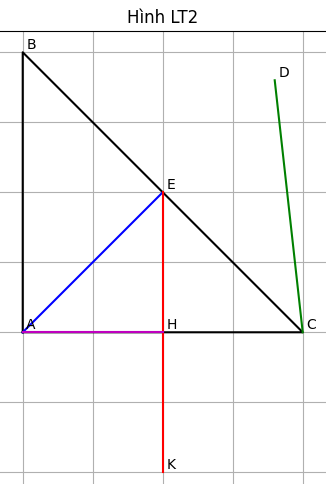
a) Chứng minh: AE ⟂ BC
E là trung điểm BC ⇒ BE = EC.
- Xét ΔABE và ΔACE:
AB = AC (giả thiết)
BE = EC (E trung điểm BC)
AE chung
⇒ ΔABE = ΔACE (c.g.c)
=> là góc kề bù 0 và bằng nhau ⇒ mỗi góc = 90°.
⇒ AE ⟂ BC.
b) Chứng minh: AC ⟂ CD
- Trên tia AE lấy D sao cho AE = ED.
- Xét ΔAED và ΔCEA, ta có :
AE = ED (giả thiết)
1(E là trung điểm nên BE = EC → tam giác ABE = ACE → 2)
EA chung
⇒ ΔAED = ΔCEA (c.g.c)
=> 3 là hai góc kề bù và bằng nhau ⇒ mỗi góc = 90°.
⇒ AC ⟂ CD.
c) Chứng minh: AH là tia phân giác của 4
- H là trung điểm AC ⇒ AH là đường trung tuyến.
- Trên tia EH lấy K sao cho EH = HK.
⇒ H là trung điểm EK (do H nằm giữa E và K & hai đoạn bằng nhau).
⇒ AH là đường trung tuyến của tam giác AEK.
- Trong ΔATE (A bất kỳ): trung tuyến từ A ứng với cạnh EK đi qua trung điểm H ⇒ hai tam giác AHE và AHK có:
AH chung
HE = HK
AE = AK (vì ΔABE = ΔACE ban đầu)
→ ΔAHE = ΔAHK (c.c.c)
⇒ 5
⇒ AH là tia phân giác của 4.
a) Hai tam giác ABM và ACM bằng nhau theo ba cạnh. Suy ra hai góc AMB và CMA kề bù. Vậy AM vuông BC.
b) AD bằng AE và AM là phân giác nên hai tam giác AMD và AME bằng nhau. Suy ra MD bằng ME và DE song song BC.
c) ME bằng MN và MD bằng ME nên M cách đều D E N. Từ đó suy ra DN song song AM.
LT2
a) Hai tam giác ABE và ACE bằng nhau theo ba cạnh. Suy ra hai góc AEB và AEC đều là góc vuông nên AE vuông BC.
b) AE bằng ED nên E là trung điểm AD. Do B và C đối xứng qua AE nên AC vuông CD.
c) H là trung điểm AC. EH bằng HK nên H là trung điểm EK. E và K đối xứng qua AH nên AH là tia phân giác góc EAK.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8458
Đã trả lời bởi chuyên gia
8458 -
 Đã trả lời bởi chuyên gia
7529
Đã trả lời bởi chuyên gia
7529 -
6460
-
 Đã trả lời bởi chuyên gia
6435
Đã trả lời bởi chuyên gia
6435 -
 Đã trả lời bởi chuyên gia
6264
Đã trả lời bởi chuyên gia
6264 -
 Đã trả lời bởi chuyên gia
6186
Đã trả lời bởi chuyên gia
6186


