Question

Đã trả lời bởi chuyên gia

Answer 1

Chào bạn! Đây là một bài toán hình học về tam giác cân và tính chất đối xứng.

📐 Hình vẽ, Giả thiết và Kết luận
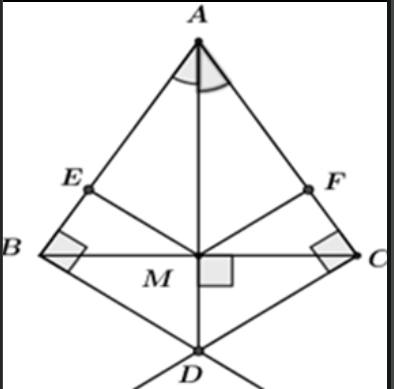
1. Hình vẽ
2. Giả thiết (GT)
$\triangle ABC$ cân tại $A$ (tức là $AB = AC$ và $\angle B = \angle C$).
$M$ là trung điểm của $BC$ (tức là $MB = MC$).
$ME \perp AB$ tại $E$.
$MF \perp AC$ tại $F$.
3. Kết luận (KL)
a. $AM$ là trung trực của $BC$ (Đây là một lỗi đánh máy, $AM$ là trung tuyến nên phải là trung trực của $BC$, nhưng dựa theo yêu cầu chứng minh, có lẽ bạn muốn hỏi $AM$ là trung trực của $BC$ hoặc $AM$ là phân giác của $\angle BAC$ vì $AM$ không thể là trung trực của $AB$). Ta sẽ chứng minh $AM$ là trung trực của $BC$.

b. $ME = MF$ và $AM$ là trung trực của $EF$.

c. $EF \parallel BC$.

✍️ Chứng minh
a. Chứng minh $AM$ là trung trực của $BC$
Vì $\triangle ABC$ cân tại $A$ và $M$ là trung điểm của cạnh đáy $BC$, nên $AM$ vừa là đường trung tuyến, vừa là đường cao, và vừa là đường phân giác.

$AM$ là đường cao $\Rightarrow AM \perp BC$.
$M$ là trung điểm của $BC$.
Một đường thẳng đi qua trung điểm của một đoạn thẳng và vuông góc với đoạn thẳng đó chính là đường trung trực.

$\Rightarrow \mathbf{AM \text{ là trung trực của } BC.}$
b. Chứng minh $ME = MF$ và $AM$ là trung trực của $EF$
Phần 1: Chứng minh $ME = MF$
Vì $\triangle ABC$ cân tại $A$, $AM$ là đường trung tuyến ứng với cạnh đáy nên $AM$ cũng là đường phân giác của $\angle BAC$.

$AM$ là phân giác của $\angle BAC$.
$ME \perp AB$ (khoảng cách từ $M$ đến $AB$).
$MF \perp AC$ (khoảng cách từ $M$ đến $AC$).
Theo tính chất đường phân giác, một điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

$\Rightarrow \mathbf{ME = MF}$
Phần 2: Chứng minh $AM$ là trung trực của $EF$
Xét $\triangle AME$ và $\triangle AMF$:

$ME = MF$ (đã chứng minh ở trên).
$\angle AEM = \angle AFM = 90^\circ$ (Giả thiết $ME \perp AB, MF \perp AC$).
$AM$ là cạnh chung.
Do đó, $\triangle AME = \triangle AMF$ (cạnh huyền - cạnh góc vuông).

$\Rightarrow AE = AF$
Vì $AE = AF$, nên điểm $A$ cách đều hai đầu đoạn thẳng $E$ và $F$.
Vì $ME = MF$, nên điểm $M$ cách đều hai đầu đoạn thẳng $E$ và $F$.
Hai điểm $A$ và $M$ cùng cách đều hai đầu đoạn thẳng $EF$. Do đó, đường thẳng $AM$ là đường trung trực của đoạn thẳng $EF$.

$\Rightarrow \mathbf{AM \text{ là trung trực của } EF.}$
c. Chứng minh $EF \parallel BC$
Trong $\triangle ABC$, ta có $AE = AF$ (chứng minh ở phần b).

$\Rightarrow \triangle AEF \text{ là tam giác cân tại } A.$
Trong $\triangle AEF$ cân tại $A$, ta có:

$\angle AFE = \frac{180^\circ - \angle A}{2} \quad (*)$
Trong $\triangle ABC$ cân tại $A$, ta có:

$\angle ACB = \frac{180^\circ - \angle A}{2} \quad (**)$
Từ $(*)$ và $(**)$ suy ra:

$\angle AFE = \angle ACB$
Hai góc $\angle AFE$ và $\angle ACB$ ở vị trí đồng vị (hoặc so le trong nếu kéo dài $EF$ và $BC$) khi $EF$ và $BC$ bị cắt bởi cát tuyến $AC$.

Do $\angle AFE = \angle ACB$, nên:

$\Rightarrow \mathbf{EF \parallel BC.}$

...Xem thêm

Answer 2