Cho hình chữ nhật ABCD, AB > AD, gọi M là trung điểm cạnh AB, từ M kẻ MN vuông góc với CD tại N
a, CM tứ giác AMND là hình chữ nhật
b, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. CM tứ giác ADBK là hình bình hành
c, Chứng minh tam giác AKC cân
(vẽ hình)
Quảng cáo
2 câu trả lời 271
`a`.Ta có: $\widehat{MAD}=\widehat{ADN}=\widehat{MND}=90^o\to ADNM$ là hình chữ nhật
`b và c.`Ta có: `AB\cap DK=M` là trung điểm mỗi đường
`\to ADBK` là hình bình hành
`\to AK=BD`
Mà `BD=AC\to AK=AC\to \Delta AKC` cân tại `A`
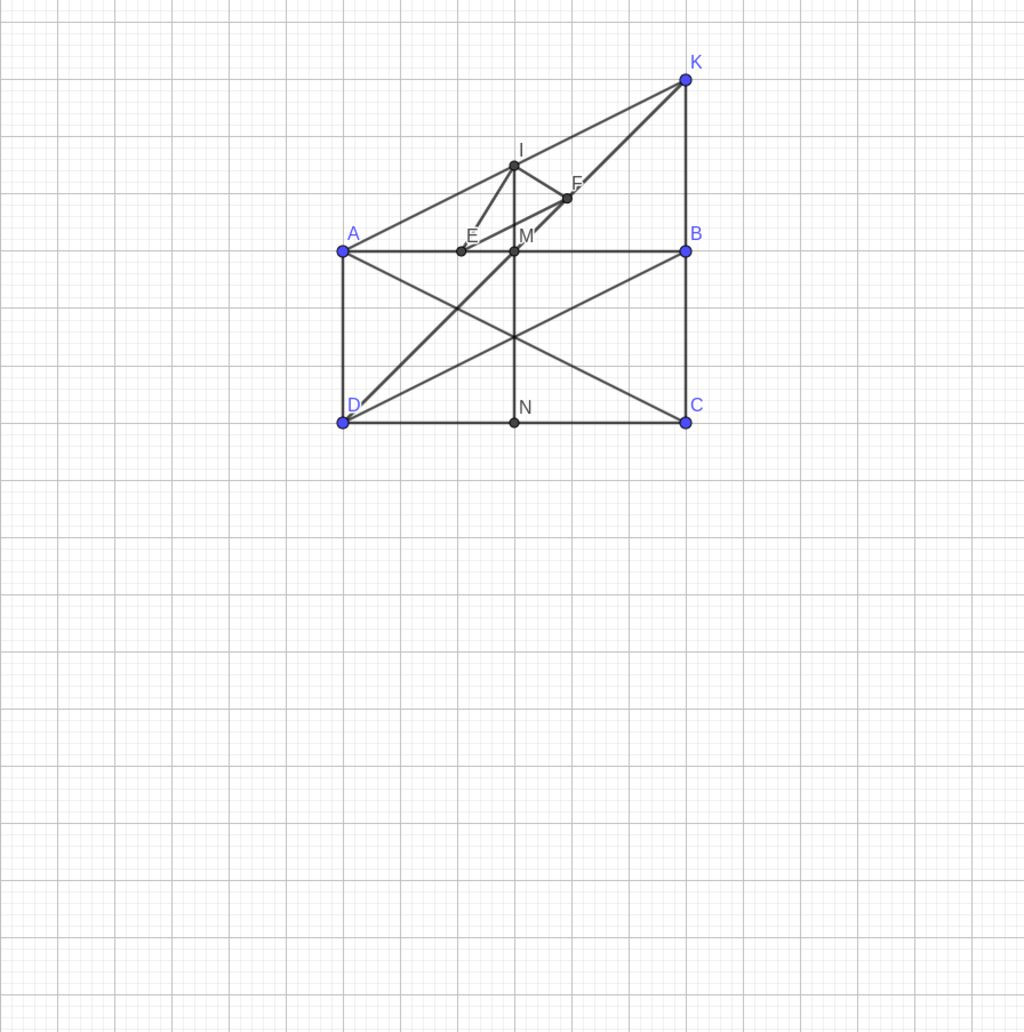
a, Chứng minh tứ giác AMND là hình chữ nhật
Tứ giác AMND có AM∥DN (do AB∥CD), Â=90∘ (do ABCD là hình chữ nhật), và N̂=90∘ (do MN⟂CD). Một tứ giác có ba góc vuông là hình chữ nhật.
b, Chứng minh tứ giác ADBK là hình bình hành
Tứ giác ADBK có hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường (theo giả thiết). Do đó, ADBK là hình bình hành theo dấu hiệu nhận biết.
c, Chứng minh tam giác AKC cân
Vì ADBK là hình bình hành nên AK=DB. Vì ABCD là hình chữ nhật nên hai đường chéo bằng nhau, DB=AC. Từ đó suy ra AK=AC. Tam giác AKC có hai cạnh AK và AC bằng nhau nên là tam giác cân tại đỉnh A
sorry mik ko vẽ hình đc
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
10861
-
 Đã trả lời bởi chuyên gia
3934
Đã trả lời bởi chuyên gia
3934



