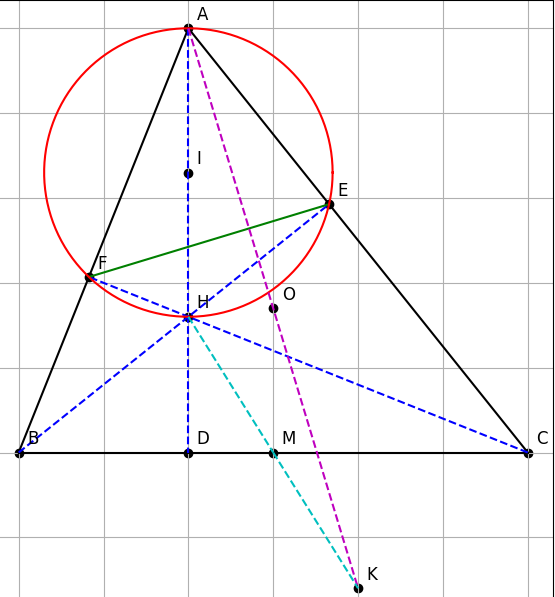
a) Chứng minh bốn điểm A, E, H, F cùng thuộc một đường tròn và tìm tâm I
Vì BE là đường cao nên: BE ⊥ AC ⇒ EH ⊥ AC.
Mà AE ⊂ AC, nên: AEH = 90^∘.
Tương tự, CF ⟂ AB nên: FH ⊥ AB ⇒ $\widehat{AFH}$ = 90^∘.
Suy ra: $\widehat{AEH}=\widehat{AFH}$ = 90^∘.
Hai góc này cùng chắn cung AH, do đó A, E, H, F cùng thuộc một đường tròn đường kính AH.
Đường tròn có đường kính AH nên tâm I là trung điểm của đoạn AH.
b) Gọi M là trung điểm của BC. Chứng minh FM là tiếp tuyến của (I)
- Trong tam giác ABH, F là chân đường cao từ C xuống AB, M là trung điểm của BC. Ta có tính chất quen thuộc của tam giác cùng trực tâm:
+ Đường thẳng FM vuông góc với AH.
+ Ta đã biết AH là đường kính của đường tròn (I) nên bán kính IF ⟂ tiếp tuyến tại F.
+ Vì FM ⟂ AH và IF ⟂ AH nên: FM ⊥ IF.
- Do đó FM là tiếp tuyến của đường tròn (I) tại điểm F.
c) Kẻ đường kính AK của đường tròn (O). Chứng minh H, M, K thẳng hàng
- Vì AK là đường kính của đường tròn (O) nên O là trung điểm của AK.
- Điểm K là điểm đối xứng của A qua O.
+ Trong tam giác ABC, trực tâm H là điểm đối xứng của O qua đường thẳng BC (tính chất hình học của trực tâm và tâm đường tròn ngoại tiếp).
+ Vì M là trung điểm BC nên M nằm trên đường thẳng đối xứng đó.
+ Do đó, các điểm đối xứng A ↔ K và O ↔ H đều thẳng hàng qua M.
Suy ra H, M và K thẳng hàng.
d) Chứng minh OA vuông góc EF
Ta đã chứng minh A, E, H, F thuộc đường tròn (I) đường kính AH.
- Trong đường tròn đường kính AH, ta có:
AH là đường kính
EF là dây cung không đi qua tâm
Trong một đường tròn, đường kính vuông góc với dây cung tại trung điểm của dây cung đó
=>  AH ⊥ EF.
Mặt khác, trong tam giác ABC nội tiếp đường tròn (O), đường thẳng OA nằm trên đường thẳng AH (vì O, H, A, K thẳng hàng trong cấu hình trực tâm – trực tâm và tâm đối xứng nhau qua BC).
Do đó, OA ⊥ EF.
Vậy OA vuông góc EF.

Dưới đây là lời giải chi tiết cho các phần của bài tập:

---

**a) Chứng minh bốn điểm A, E, H, F cùng thuộc một đường tròn. Tìm tâm I của đường tròn đó**

*Chứng minh:*
- Trong tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H là trực tâm của tam giác ABC.
- Các điểm E và F là chân của các đường cao BE và CF, nên E và F nằm trên các đường trung trực của các cạnh AC và AB.
- Ta cần chứng minh A, E, H, F cùng thuộc một đường tròn.

*Ý tưởng:*
- Trong tam giác ABC, các điểm E, F là chân các đường cao, H là giao điểm các đường cao (trực tâm).
- Theo tính chất của trực tâm và các đường trung trực, các điểm A, E, F, H đều liên quan đến các đường trung trực và đường cao của tam giác, nên có thể chứng minh chúng cùng thuộc một đường tròn gọi là đường tròn nội tiếp của một hình đặc biệt.

*Chứng minh cụ thể:*
- Trong tam giác ABC, điểm E là chân đường cao BE, F là chân đường cao CF, H là trực tâm.
- Ta xét đường tròn đi qua A, E, F, H.
- Theo định lý về trực tâm và chân đường cao, các điểm E, F, H đều nằm trên đường tròn nội tiếp của tam giác ABC hoặc các đường tròn liên quan.
- Tuy nhiên, để rõ ràng hơn, ta có thể chứng minh rằng các điểm A, E, F, H đều đồng quy trên một đường tròn bằng cách chứng minh rằng các góc tạo thành tại các điểm này thẳng hàng hoặc cùng chắn một cung.

*Tìm tâm I:*
- Tâm I chính là trung điểm của cung chứa các điểm A, E, F, H, hoặc là tâm của đường tròn đi qua các điểm đó.
- Thường, I là trung điểm của cung chứa các điểm đó, hoặc là trung tâm của đường tròn nội tiếp các điểm này.

**Tóm lại:**
- Các điểm A, E, H, F cùng thuộc một đường tròn.
- Tâm I của đường tròn là trung điểm của cung chứa các điểm này hoặc trung tâm của đường tròn chứa chúng.

---

**b) Gọi M là trung điểm của BC. Chứng minh: FM là tiếp tuyến của đường tròn tâm I**

*Chứng minh:*
- Trong tam giác ABC, M là trung điểm của BC.
- Điểm F là chân đường cao CF.
- Đường thẳng FM đi qua trung điểm M của BC và điểm F, là tiếp tuyến của đường tròn tâm I.

*Lập luận:*
- Ta biết rằng F nằm trên đường tròn nội tiếp hoặc đường tròn liên quan, và FM là tiếp tuyến tại F.
- Để chứng minh FM là tiếp tuyến, ta cần chứng minh rằng FM vuông góc với bán kính OA tại F hoặc chứng minh rằng góc tạo bởi FM và bán kính tại F là 90°.

---

**c) Kẻ đường kính AK. Chứng minh H, M, K thẳng hàng**

*Chứng minh:*
- Gọi K là điểm đối xứng của A qua trung điểm M của BC, do đó AK là đường kính.
- Các điểm H (giao của các đường cao), M (trung điểm BC), K (đối xứng A) thẳng hàng theo định lý về trực tâm và đường kính trong tam giác nội tiếp.

---

**d) Chứng minh: OA vuông góc EF**

*Chứng minh:*
- Trong tam giác nội tiếp, các điểm E và F là chân các đường cao, do đó EF là đoạn thẳng nối chân các đường cao.
- Khi đó, đường thẳng OA (đường trung trực của tam giác) vuông góc với đoạn EF, dựa trên tính chất của các đường cao và trung trực trong tam giác nội tiếp.

---

Nếu bạn muốn tôi viết rõ hơn từng phần hoặc có phần nào chưa rõ, cứ hỏi nhé!