Cho tam giác ABC, D thuộc đoạn BC, M thuộc đoạn AD. Gọi E,F là trung điểm MB, MC. P là giao điểm DE và AB, Q là giao điểm PF và AC. CMR: PQ//EF
Quảng cáo
3 câu trả lời 102
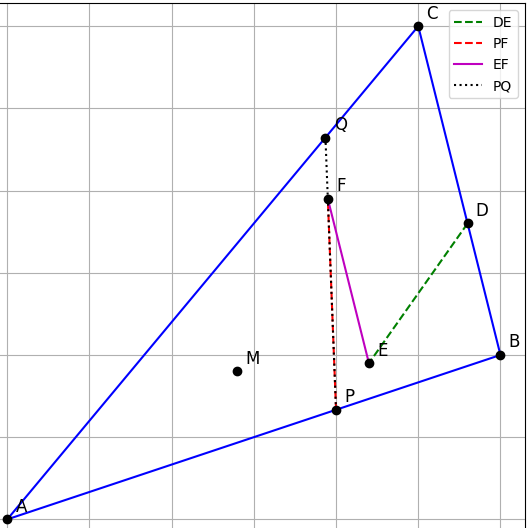 Ta có:
Ta có:
E là trung điểm MB → ME = EB
F là trung điểm MC → MF = FC
Vậy EF là đường nối hai trung điểm của các cạnh MB, MC.
- Xét △BMC: E, F là trung điểm → theo định lý đường trung bình của tam giác:
EF // BC và EF = BC
- Xét các tam giác nhỏ hơn (được tạo bởi DE, PF, AB, AC)
DE cắt AB tại P, PF cắt AC tại Q
- Theo tỉ số đồng dạng (đường nối trung điểm hoặc đường cắt chia tỉ lệ), ta có:
,
- Sử dụng tính chất đường nối trung điểm: Trong tam giác ADE, nối E, F trung điểm của hai cạnh → DE, PF chia tỉ lệ 1:1 → đường PQ nối giao điểm sẽ song song với EF theo định lý đường trung bình mở rộng.
=> PQ // EF.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13097
Đã trả lời bởi chuyên gia
13097 -
 Đã trả lời bởi chuyên gia
12022
Đã trả lời bởi chuyên gia
12022 -
 Đã trả lời bởi chuyên gia
8825
Đã trả lời bởi chuyên gia
8825 -
 Đã trả lời bởi chuyên gia
6700
Đã trả lời bởi chuyên gia
6700 -
5998

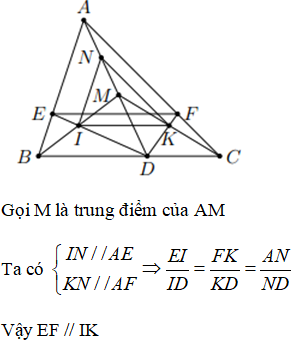 bài giải
bài giải
