Hùng Vũ Mạnh
Hỏi từ APP VIETJACK
cho tam giác ABC cân tại A, đường trung tuyến AH. Gọi Ô là trung điểm của AC, D là điểm đối xứng với H qua O
a, c/m tứ giác AHCD là hình chữ nhật
b, Tứ giác ADHB là hình gì? Vì sao?
mn ơi giải gấp hộ mình vs ạ
a, c/m tứ giác AHCD là hình chữ nhật
b, Tứ giác ADHB là hình gì? Vì sao?
mn ơi giải gấp hộ mình vs ạ
Quảng cáo
3 câu trả lời 640
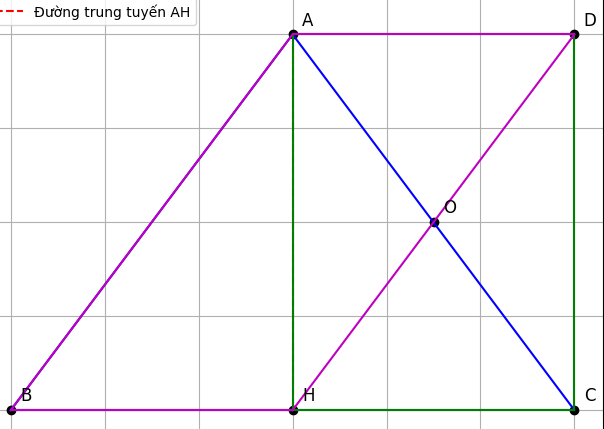
a) Chứng minh tứ giác AHCD là hình chữ nhật.
Tam giác ABC cân tại A nên AB = AC.
AH là đường trung tuyến nên H là trung điểm của BC.
O là trung điểm của AC.
D là điểm đối xứng với H qua O nên O là trung điểm của đoạn HD.
Vậy trong tứ giác AHCD, hai đường chéo AC và HD cắt nhau tại O, mà O là trung điểm của cả hai.
Tam giác ABC cân tại A nên AB = AC.
AH là đường trung tuyến nên H là trung điểm của BC.
O là trung điểm của AC.
D là điểm đối xứng với H qua O nên O là trung điểm của đoạn HD.
Vậy trong tứ giác AHCD, hai đường chéo AC và HD cắt nhau tại O, mà O là trung điểm của cả hai.
Điều này chứng tỏ AHCD là hình bình hành.
Do tam giác ABC cân tại A, đường trung tuyến AH đồng thời là đường cao → AH ⊥ BC.
Từ đó, AH ⊥ BC ⇒ AH ⊥ HC.
Vì AH ⊥ HC và HCHCHC là cạnh của tứ giác AHCD, suy ra AH ⊥ CD.
Trong hình bình hành AHCD, nếu một góc vuông thì tứ giác đó là hình chữ nhật.
Vậy AHCD là hình chữ nhật.
b) Tứ giác ADHB là hình gì? Vì sao?
D là điểm đối xứng của H qua O, nên OD = OH.
O là trung điểm của AC, H là trung điểm của BC.
Khi xét tứ giác ADHB, ta thấy hai đoạn thẳng AD và BH song song và bằng nhau (do đối xứng).
Hai đoạn AB và DH cũng song song.
Vì vậy, tứ giác ADHB có hai cặp cạnh đối song song và bằng nhau, nên ADHB là hình bình hành.
Do tam giác ABC cân tại A, đường trung tuyến AH đồng thời là đường cao → AH ⊥ BC.
Từ đó, AH ⊥ BC ⇒ AH ⊥ HC.
Vì AH ⊥ HC và HCHCHC là cạnh của tứ giác AHCD, suy ra AH ⊥ CD.
Trong hình bình hành AHCD, nếu một góc vuông thì tứ giác đó là hình chữ nhật.
Vậy AHCD là hình chữ nhật.
b) Tứ giác ADHB là hình gì? Vì sao?
D là điểm đối xứng của H qua O, nên OD = OH.
O là trung điểm của AC, H là trung điểm của BC.
Khi xét tứ giác ADHB, ta thấy hai đoạn thẳng AD và BH song song và bằng nhau (do đối xứng).
Hai đoạn AB và DH cũng song song.
Vì vậy, tứ giác ADHB có hai cặp cạnh đối song song và bằng nhau, nên ADHB là hình bình hành.
3 tháng trước
a. Tứ giác AHCD là hình chữ nhật
- Tam giác ABC cân tại A, AH là đường trung tuyến:
- Trong tam giác cân ABC tại A, đường trung tuyến AH đồng thời là đường cao và đường phân giác.
- Do đó, AH vuông góc với BC, hay góc AHC = 90 độ.
- O là trung điểm của AC:
- Vì O là trung điểm của AC, nên AO = OC.
- D đối xứng với H qua O:
- Điều này có nghĩa là O là trung điểm của đoạn thẳng HD.
- Do đó, HO = OD.
- Xét tứ giác AHCD:
- Hai đường chéo AC và HD cắt nhau tại trung điểm O.
- Vì vậy, AHCD là hình bình hành.
- Mặt khác, tam giác ABC cân tại A, AH là đường trung tuyến, H thuộc BC. O là trung điểm của AC. D đối xứng với H qua O nên O là trung điểm của HD.
- Mà tam giác ABC cân tại A, AH là đường cao nên AH vuông góc với BC.
- AHCD có hai đường chéo AC và HD cắt nhau tại O, mà HO = OD, AO = OC.
- Do đó, AHCD là hình bình hành có hai đường chéo cắt nhau tại trung điểm O.
- AC là đường chéo.
- AHCD là hình chữ nhật vì có góc AHC = 90 độ.
b. Tứ giác ADHB là hình gì? Vì sao?
- AD // BH và AD = BH:
- Vì D đối xứng với H qua O, nên O là trung điểm của HD.
- Trong tam giác ABC, O là trung điểm của AC. AH là đường trung tuyến.
- Trong tam giác AHC, O là trung điểm của AC và D là trung điểm của HD. Do đó, DO // HC.
- Tuy nhiên, ta có thể chứng minh ADHB là hình bình hành theo cách khác:
- ADHB là hình bình hành vì D đối xứng với H qua O và O là trung điểm của AC. Do đó, AH // BD và AH = BD.
- Tam giác ABC cân tại A, AH là trung tuyến nên AH = HC.
- Suy ra BD = AH = HC.
- Tứ giác ADHB có:
- AD // BH (do D đối xứng với H qua O)
- AH // DB (do O là trung điểm của AC và HD)
- Do đó, tứ giác ADHB là hình bình hành.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103198
-
Hỏi từ APP VIETJACK78870
-
Hỏi từ APP VIETJACK71786
-
Hỏi từ APP VIETJACK60081
-
Hỏi từ APP VIETJACK45961
-
36820
Thành viên hăng hái nhất trong tuần
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8220
-
3 năm trước7732
-
3 năm trước6571
-
3 năm trước6459
-
3 năm trước6291
Gửi báo cáo thành công!
