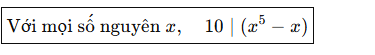Minh Phương Nguyễn Huỳnh
Hỏi từ APP VIETJACK
Chứng minh: x⁵ - x chia hết 10
Quảng cáo
3 câu trả lời 156
Chứng minh x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 1010
10
Phân tích biểu thức
Biểu thức x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
có thể được phân tích thành nhân tử như sau:
x5−x=x(x4−1)=x(x2−1)(x2+1)=x(x−1)(x+1)(x2+1)x raised to the exponent 5 end-exponent minus x equals x open paren x raised to the exponent 4 end-exponent minus 1 close paren equals x open paren x squared minus 1 close paren open paren x squared plus 1 close paren equals x open paren x minus 1 close paren open paren x plus 1 close paren open paren x squared plus 1 close paren
𝑥5−𝑥=𝑥(𝑥4−1)=𝑥(𝑥2−1)(𝑥2+1)=𝑥(𝑥−1)(𝑥+1)(𝑥2+1)
.
Chứng minh chia hết cho 22
2
Tích x(x−1)(x+1)x open paren x minus 1 close paren open paren x plus 1 close paren
𝑥(𝑥−1)(𝑥+1)
là tích của ba số nguyên liên tiếp. Trong ba số nguyên liên tiếp, luôn có ít nhất một số chẵn. Do đó, tích x(x−1)(x+1)x open paren x minus 1 close paren open paren x plus 1 close paren
𝑥(𝑥−1)(𝑥+1)
luôn chia hết cho 22
2
.
Vì x(x−1)(x+1)x open paren x minus 1 close paren open paren x plus 1 close paren
𝑥(𝑥−1)(𝑥+1)
là một nhân tử của x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
, nên x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
luôn chia hết cho 22
2
.
Chứng minh chia hết cho 55
5
Có thể xét các trường hợp của xx
𝑥
theo modulo 55
5
:
\begin{enumerate}
\item Nếu x≡0(mod5)x triple bar 0 space open paren mod 5 close paren
𝑥≡0(mod5)
, thì xx
𝑥
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡1(mod5)x triple bar 1 space open paren mod 5 close paren
𝑥≡1(mod5)
, thì x−1x minus 1
𝑥−1
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡4(mod5)x triple bar 4 space open paren mod 5 close paren
𝑥≡4(mod5)
, hay x≡-1(mod5)x triple bar negative 1 space open paren mod 5 close paren
𝑥≡−1(mod5)
, thì x+1x plus 1
𝑥+1
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡2(mod5)x triple bar 2 space open paren mod 5 close paren
𝑥≡2(mod5)
, thì x2+1=22+1=5x squared plus 1 equals 2 squared plus 1 equals 5
𝑥2+1=22+1=5
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡3(mod5)x triple bar 3 space open paren mod 5 close paren
𝑥≡3(mod5)
, thì x2+1=32+1=10x squared plus 1 equals 3 squared plus 1 equals 10
𝑥2+1=32+1=10
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\end{enumerate}
Trong mọi trường hợp, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
luôn chia hết cho 55
5
.
Kết luận
Vì x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 22
2
và x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
, mà 22
2
và 55
5
là hai số nguyên tố cùng nhau, nên x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho tích của chúng là 2×5=102 cross 5 equals 10
2×5=10
.
Kết quả cuối cùng
Biểu thức x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
luôn chia hết cho 1010
10
.
𝑥5−𝑥
chia hết cho 1010
10
Phân tích biểu thức
Biểu thức x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
có thể được phân tích thành nhân tử như sau:
x5−x=x(x4−1)=x(x2−1)(x2+1)=x(x−1)(x+1)(x2+1)x raised to the exponent 5 end-exponent minus x equals x open paren x raised to the exponent 4 end-exponent minus 1 close paren equals x open paren x squared minus 1 close paren open paren x squared plus 1 close paren equals x open paren x minus 1 close paren open paren x plus 1 close paren open paren x squared plus 1 close paren
𝑥5−𝑥=𝑥(𝑥4−1)=𝑥(𝑥2−1)(𝑥2+1)=𝑥(𝑥−1)(𝑥+1)(𝑥2+1)
.
Chứng minh chia hết cho 22
2
Tích x(x−1)(x+1)x open paren x minus 1 close paren open paren x plus 1 close paren
𝑥(𝑥−1)(𝑥+1)
là tích của ba số nguyên liên tiếp. Trong ba số nguyên liên tiếp, luôn có ít nhất một số chẵn. Do đó, tích x(x−1)(x+1)x open paren x minus 1 close paren open paren x plus 1 close paren
𝑥(𝑥−1)(𝑥+1)
luôn chia hết cho 22
2
.
Vì x(x−1)(x+1)x open paren x minus 1 close paren open paren x plus 1 close paren
𝑥(𝑥−1)(𝑥+1)
là một nhân tử của x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
, nên x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
luôn chia hết cho 22
2
.
Chứng minh chia hết cho 55
5
Có thể xét các trường hợp của xx
𝑥
theo modulo 55
5
:
\begin{enumerate}
\item Nếu x≡0(mod5)x triple bar 0 space open paren mod 5 close paren
𝑥≡0(mod5)
, thì xx
𝑥
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡1(mod5)x triple bar 1 space open paren mod 5 close paren
𝑥≡1(mod5)
, thì x−1x minus 1
𝑥−1
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡4(mod5)x triple bar 4 space open paren mod 5 close paren
𝑥≡4(mod5)
, hay x≡-1(mod5)x triple bar negative 1 space open paren mod 5 close paren
𝑥≡−1(mod5)
, thì x+1x plus 1
𝑥+1
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡2(mod5)x triple bar 2 space open paren mod 5 close paren
𝑥≡2(mod5)
, thì x2+1=22+1=5x squared plus 1 equals 2 squared plus 1 equals 5
𝑥2+1=22+1=5
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\item Nếu x≡3(mod5)x triple bar 3 space open paren mod 5 close paren
𝑥≡3(mod5)
, thì x2+1=32+1=10x squared plus 1 equals 3 squared plus 1 equals 10
𝑥2+1=32+1=10
chia hết cho 55
5
. Do đó, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
.
\end{enumerate}
Trong mọi trường hợp, x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
luôn chia hết cho 55
5
.
Kết luận
Vì x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 22
2
và x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho 55
5
, mà 22
2
và 55
5
là hai số nguyên tố cùng nhau, nên x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
chia hết cho tích của chúng là 2×5=102 cross 5 equals 10
2×5=10
.
Kết quả cuối cùng
Biểu thức x5−xx raised to the exponent 5 end-exponent minus x
𝑥5−𝑥
luôn chia hết cho 1010
10
.
Hi các bn
phạm anh tuấn
· 3 tháng trước
Ủa đau hết r đùa nhau chắc
phạm anh tuấn
· 3 tháng trước
Tôi kêu nt ở đây mà
huhu
· 3 tháng trước
ê tuấn
huhu
· 3 tháng trước
ngủ ít thuiii
huhu
· 3 tháng trước
dậy reppp ik
huhu
· 3 tháng trước
ko nhắn e dỗiiiiii á
huhu
· 3 tháng trước
huhu
huhu
· 3 tháng trước
huhu
huhu
· 3 tháng trước
cayyyyyyyy lắm ruiii đấy nhá
huhu
· 3 tháng trước
tuấn oiiiii
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
103475
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
79181
Đã trả lời bởi chuyên gia
79181 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
72519
Đã trả lời bởi chuyên gia
72519 -
Hỏi từ APP VIETJACK60307
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
46296
Đã trả lời bởi chuyên gia
46296 -
 Đã trả lời bởi chuyên gia
36999
Đã trả lời bởi chuyên gia
36999
Gửi báo cáo thành công!