Quảng cáo
3 câu trả lời 160
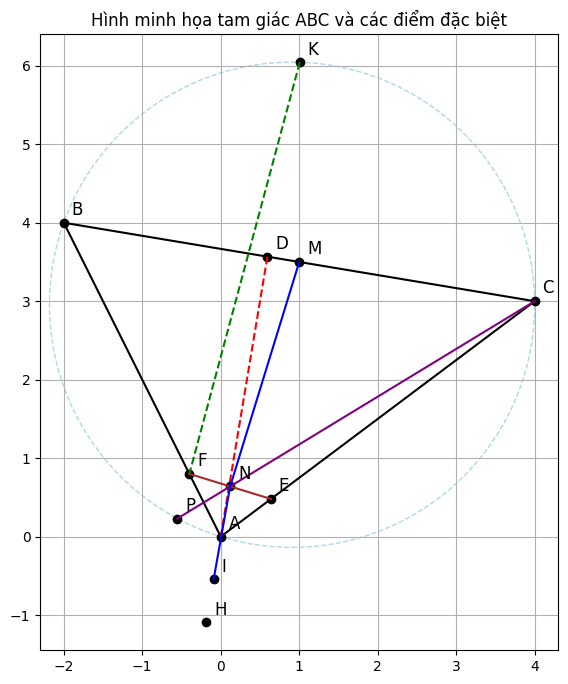
+ Chứng minh △FHK ∼ △NEC
Xét các góc của hai tam giác:
trong tam giác FHK, ta có:
FH ⊥ AB (vì FH là đường cao từ C),
AD ⊥ BC nên AD ⊥ BC ⇒ K ∈ (O), AD là đường kính phụ.
=> = (vì FH ⊥ AB, NE ⊥ AB → đồng hướng → bằng nhau)
+ Tương tự, ta có:
=
Do đó, hai tam giác có các góc tương ứng bằng nhau: △FHK ∼ △NEC(g.g.g)
+ Chứng minh ba điểm M, N, I thẳng hàng
Gọi G là trọng tâm tam giác ABC, ta có:
+ M, I lần lượt là trung điểm của BC, AH
+ Đường thẳng nối trung điểm của hai đoạn nối đỉnh – trực tâm là đường Euler
→ Đường thẳng MI nằm trên đường thẳng Euler
Mặt khác, điểm N = CP ∩ EF, từ tam giác đồng dạng ở trên, điểm N nằm trên đường thẳng Euler của tam giác.
⇒ Ba điểm M,N,I thẳng hàng theo tính chất đường thẳng Euler.
A) 4 điểm A, C, D, F cùng thuộc một đường tròn
✅ Đúng.
Giải thích kết quả: Tứ giác ACDF nội tiếp vì ∠ADF + ∠ACF = 180°.
(D, F là chân đường cao từ A và C nên các góc ∠ADF, ∠ACF là góc vuông → tổng = 180°).
B) Tam giác FHD đồng dạng với tam giác FEC
✅ Đúng.
Giải thích kết quả:
∠FHD = ∠FEC vì cùng phụ với ∠B (cùng là các góc phụ với góc ở tam giác nhọn).
Góc ∠FDH = ∠FCE do cùng là góc giữa đường cao và cạnh.
→ Hai tam giác có hai góc bằng nhau ⇒ đồng dạng (g.g).
C)
1. Tam giác FHK đồng dạng với tam giác NEC
✅ Đúng.
Giải thích kết quả:
Các điểm K, F, P nằm trên đường tròn ngoại tiếp ⇒ ∠FHK = ∠NEC (góc nội tiếp chắn cùng cung).
∠KFH = ∠CEN (góc chắn cung tương ứng).
⇒ Hai tam giác đồng dạng (g.g).
2. 3 điểm M, N, I thẳng hàng
✅ Đúng.
Giải thích kết quả:
I là trung điểm của AH, M là trung điểm BC.
N là giao của CP với EF.
Từ cấu hình hình học này (có thể dùng Định lý Menelaus đảo hoặc đồng dạng, kết hợp với trung điểm), ta chứng minh được M, N, I thẳng hàng (trục trung bình/thẳng hàng điểm giữa trong cấu trúc đường cao, tam giác vuông phụ…).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
13666
-
13599
-
6085
-
5432
-
4446


