Cho tam giác ABC vuông tại A , AB = 3cm, AC=4cm
a) Tính BC
b) Trên tia đối của tia AB lấy điểm M sao cho AM = AC. Trên tia đối của tia AC lấy điểm N sao cho AN = AB. Chứng minh rằng BC = MN và NB//MC
c) Gọi I là trung điểm của MC. Chứng minh rằng tam giác BIN cân?
Quảng cáo
4 câu trả lời 261
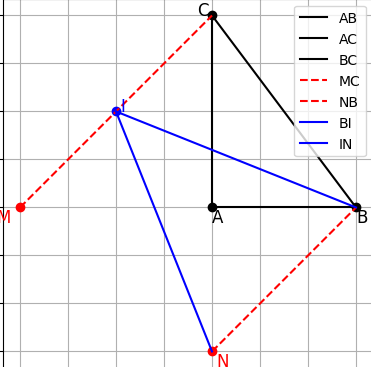
a) Tính BC
Tam giác ABC vuông tại A nên áp dụng định lý Pythagore, ta có:
BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25
⇒BC = = 5 cm
b) Chứng minh rằng BC = MN và NB // MC
Vì AM = AC = 4 cm, mà M nằm trên tia đối của AB
→ =
Tương tự, AN = AB = 3 cm, N nằm trên tia đối của AC
→ =
+ Xét hai tam giác vuông ABC và MNA có:
AB = AN
AC = AM
=
→ Hai tam giác ABC và MNA bằng nhau (theo cạnh - góc - cạnh).
=> BC = MN (đpcm)
+ Vì hai tam giác ABC và MNA bằng nhau nên = nằm ở vị trí so le trong giữa hai đường thẳng NB và MC cắt nhau bởi đường chéo MN
=> NB // MC(hai góc so le trong bằng nhau) (đpcm)
c) Gọi I là trung điểm của MC.
+ Do MC // NB, nên đoạn nối trung điểm I đến đỉnh B và N sẽ bằng nhau.
+ Xét △IBM và △ICN, ta có:
IM = IC (do I là trung điểm của MC)
BM = CN (do hai tam giác ABC và MNA bằng nhau)
= 0 (đối đỉnh)
→ Hai tam giác IBM và ICN bằng nhau (c.g.c)
=> IB = IN
⇒△BIN cân tại I (đpcm)
a.5cm
b.NB//MC
c.BIN cân tại I
A. Xét ABC vuông tại A có:
BC=AB mũ 2+AC mũ 2 "Pytago"
T/s:BC=3 mũ 2+ 4 mũ 2=25"
BC==5 cm
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
6426
-
6220


