cho tam giác ABC có góc A bằng 60 độ, các đường trung trực của AB, AC cắt nhau tại O. tính số đo góc BOC
Quảng cáo
3 câu trả lời 146
✳️ Đề bài:
Cho tam giác ABC có góc A = 60∘.
Các đường trung trực của các cạnh AB và AC cắt nhau tại O.
Tính số đo góc .
✅ Phân tích:
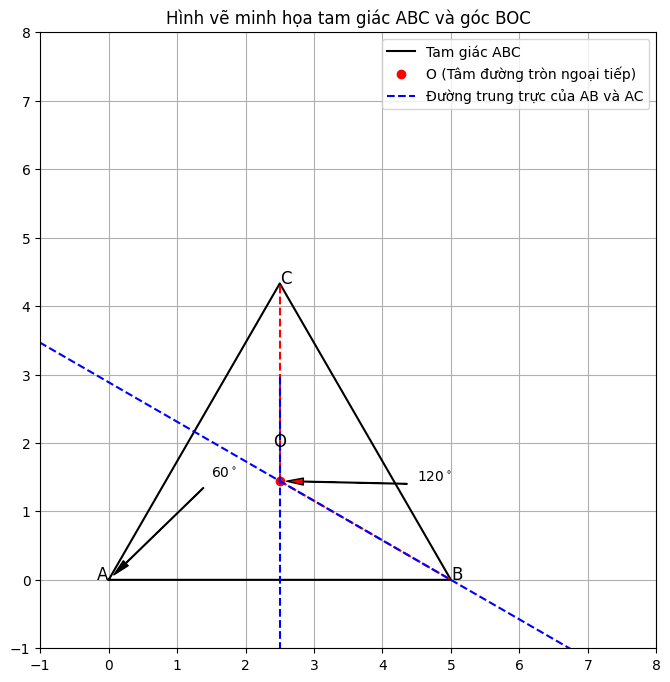
O là giao điểm các đường trung trực của AB và AC, nên:
O cách đều A và B→ OA = OB
O cách đều A và C → OA = OC
→ Suy ra: OB = OA = OC
⟹ O là tâm đường tròn ngoại tiếp tam giác ABC.
✅ Áp dụng định lý góc ở tâm và góc nội tiếp:
Vì O là tâm đường tròn ngoại tiếp tam giác ABC, nên:
Góc ở tâm chắn cung BC
Góc nội tiếp cũng chắn cung BC
⟹ Ta có: = 2⋅ = 2⋅60∘ = 120∘
Hướng dẫn giải bài toán
Để giải bài toán này, ta sẽ sử dụng các tính chất của đường trung trực và các tam giác liên quan.
1. Phân tích đề bài:
Cho tam giác ABC.
Góc A = 60°.
O là giao điểm của các đường trung trực của cạnh AB và AC.
2. Tính chất của giao điểm các đường trung trực:
Theo định nghĩa, giao điểm của các đường trung trực của một tam giác là tâm của đường tròn ngoại tiếp tam giác đó.
Khoảng cách từ tâm đường tròn ngoại tiếp đến các đỉnh của tam giác là bằng nhau.
Do O là giao điểm của các đường trung trực của AB và AC, nên O là tâm đường tròn ngoại tiếp tam giác ABC.
Suy ra, OA=OB=OC.
3. Xét các tam giác liên quan:
Vì OA=OB, tam giác OAB là tam giác cân tại O.
Vì OA=OC, tam giác OAC là tam giác cân tại O.
4. Mối quan hệ giữa góc ở tâm và góc nội tiếp:
Trong một đường tròn, góc ở tâm chắn một cung thì có số đo bằng hai lần góc nội tiếp cùng chắn cung đó.
Góc BOC là góc ở tâm, chắn cung BC.
Góc BAC (hay góc A) là góc nội tiếp, cũng chắn cung BC.
Theo tính chất trên, ta có: ∠BOC=2×∠BAC.
5. Tính toán:
Theo đề bài, ∠BAC=60∘.
Thay vào công thức trên, ta được: ∠BOC=2×60∘=120∘.
Đáp số: Số đo của góc BOC là 120∘.
Vì O là giao điểm của các đường trung trực của AB và AC, nên O là tâm đường tròn ngoại tiếp tam giác ABC. Điều này có nghĩa là OA = OB = OC.
2. Sử dụng tính chất của tâm đường tròn ngoại tiếp:
Do O là tâm đường tròn ngoại tiếp, góc BOC là góc ở tâm chắn cung BC, và góc BAC là góc nội tiếp chắn cùng cung BC.
3. Áp dụng định lý về góc ở tâm và góc nội tiếp:
Số đo góc ở tâm bằng hai lần số đo góc nội tiếp cùng chắn một cung. Do đó, ∠BOC=2×∠BA
4. Thay thế giá trị đã cho:
Vì ∠BAC=60∘
, ta có ∠BOC=2×60∘=120∘
.
Đáp số: Số đo góc BOC là 120∘
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5817
Đã trả lời bởi chuyên gia
5817 -
 Đã trả lời bởi chuyên gia
4149
Đã trả lời bởi chuyên gia
4149


