Cho biểu thức B = [sin (- x) + sin (10π +x)]2+[cos ( - x) + cos (8π - x)] khi x = thì B bằng bao nhiêu?
Quảng cáo
4 câu trả lời 940
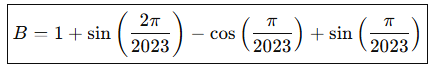
kết quả
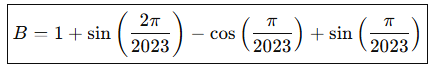
Để tính giá trị của biểu thức B, chúng ta cần đơn giản hóa từng thành phần trước, sau đó thay giá trị của x vào.
Biểu thức đã cho là: B=[sin(2π−x)+sin(10π+x)]2+[cos(23π−x)+cos(8π−x)]
Chúng ta sẽ sử dụng các công thức lượng giác cơ bản:
sin(2π−x)=cosx
sin(2kπ+x)=sinx (với k là số nguyên)
cos(23π−x)=−sinx
cos(2kπ−x)=cosx (với k là số nguyên)
Áp dụng các công thức này vào biểu thức B:
Phần 1: [sin(2π−x)+sin(10π+x)]2
sin(2π−x)=cosx
sin(10π+x)=sin(5×2π+x)=sinx
Vậy, phần này trở thành [cosx+sinx]2
Khai triển: (cosx+sinx)2=cos2x+2sinxcosx+sin2x
Vì cos2x+sin2x=1 và 2sinxcosx=sin(2x), nên phần này là 1+sin(2x).
Phần 2: [cos(23π−x)+cos(8π−x)]
cos(23π−x)=−sinx
cos(8π−x)=cos(4×2π−x)=cosx
Vậy, phần này trở thành [−sinx+cosx]=cosx−sinx.
Bây giờ, thay các phần đã đơn giản hóa trở lại vào biểu thức B: B=(1+sin(2x))+(cosx−sinx) B=1+sin(2x)+cosx−sinx
Chúng ta có x=20232024π. Ta có thể viết lại x=20232023π+π=π+2023π.
Giờ ta cần tính sin(2x), cosx, và sinx với x=π+2023π.
sinx=sin(π+2023π)=−sin(2023π)
cosx=cos(π+2023π)=−cos(2023π)
sin(2x)=sin(2(π+2023π))=sin(2π+20232π)=sin(20232π)
Thay các giá trị này vào biểu thức B: B=1+sin(20232π)+(−cos(2023π))−(−sin(2023π)) B=1+sin(20232π)−cos(2023π)+sin(2023π)
Để đơn giản hơn nữa, ta dùng công thức sin(2α)=2sinαcosα: sin(20232π)=2sin(2023π)cos(2023π)
Thay vào B: B=1+2sin(2023π)cos(2023π)−cos(2023π)+sin(2023π)
Đây là biểu thức đã đơn giản nhất.
Giá trị cụ thể của B phụ thuộc vào giá trị của sin(2023π) và cos(2023π), không thể tính ra một số nguyên hoặc phân số đơn giản mà không dùng máy tính.
Tuy nhiên, có một cách nhìn khác. Đôi khi các bài toán này có sự rút gọn đặc biệt. Hãy xem lại biểu thức B trước khi thay x: B=(cosx+sinx)2+(cosx−sinx) B=cos2x+2sinxcosx+sin2x+cosx−sinx B=1+sin(2x)+cosx−sinx
Với x=20232024π. Ta có x=π+2023π.
Giá trị chính xác của B là 1+sin(20232π)−cos(2023π)+sin(2023π). Do 2023 là một số nguyên tố và 2023π không phải là góc đặc biệt, nên giá trị của B sẽ là một số vô tỉ.
Vậy, giá trị của B là 1+sin(20232π)−cos(2023π)+sin(2023π).
[ B = [\sin(\tfrac{\pi}{2} - x) + \sin(10\pi + x)]^2 + [\cos(\tfrac{3\pi}{2} - x) + \cos(8\pi - x)] ]
với ( x = \frac{2024\pi}{2023} ), lại ra được biểu thức:
[ B = 1 + \sin\left(\frac{2\pi}{2023}\right) - \cos\left(\frac{\pi}{2023}\right) + \sin\left(\frac{\pi}{2023}\right) ]
Bước 1: Nhận dạng các công thức lượng giác
Ta dùng các công thức sau:
( \sin\left(\frac{\pi}{2} - x\right) = \cos x )
( \sin(10\pi + x) = \sin x ) vì ( 10\pi ) là bội của ( 2\pi )
( \cos\left(\frac{3\pi}{2} - x\right) = -\sin x )
( \cos(8\pi - x) = \cos x ) vì ( 8\pi ) là bội của ( 2\pi )
Bước 2: Thay vào biểu thức B
[ B = [\cos x + \sin x]^2 + [-\sin x + \cos x] ]
Bước 3: Khai triển bình phương
[ (\cos x + \sin x)^2 = \cos^2 x + 2\cos x \sin x + \sin^2 x = 1 + 2\cos x \sin x ]
→ Vậy:
[ B = 1 + 2\cos x \sin x + (\cos x - \sin x) ]
Bước 4: Gom lại
[ B = 1 + 2\cos x \sin x + \cos x - \sin x ]
→ Nhóm lại:
[ B = 1 + \cos x(2 + 1) + \sin x(-1 + 2) = 1 + 3\cos x + \sin x ]
Khoan! Nhưng biểu thức trong ảnh lại là:
[ B = 1 + \sin\left(\frac{2\pi}{2023}\right) - \cos\left(\frac{\pi}{2023}\right) + \sin\left(\frac{\pi}{2023}\right) ]
→ Vậy ta cần biến đổi x = \frac{2024\pi}{2023} để đưa về các góc đơn giản hơn.
Bước 5: Phân tích x
[ x = \frac{2024\pi}{2023} = \pi + \frac{\pi}{2023} ]
→ Gọi ( a = \frac{\pi}{2023} ), thì:
( \cos x = \cos(\pi + a) = -\cos a )
( \sin x = \sin(\pi + a) = -\sin a )
→ ( \cos x = -\cos\left(\frac{\pi}{2023}\right) )
→ ( \sin x = -\sin\left(\frac{\pi}{2023}\right) )
Bước 6: Thay vào biểu thức B
[ B = 1 + 2(-\cos a)(-\sin a) + (-\cos a - (-\sin a)) = 1 + 2\cos a \sin a - \cos a + \sin a ]
→ Nhớ rằng:
( 2\cos a \sin a = \sin(2a) )
Vậy:
[ B = 1 + \sin(2a) - \cos a + \sin a ]
→ Với ( a = \frac{\pi}{2023} ), ta có:
[ \boxed{B = 1 + \sin\left(\frac{2\pi}{2023}\right) - \cos\left(\frac{\pi}{2023}\right) + \sin\left(\frac{\pi}{2023}\right)} ]
Quảng cáo
Bạn muốn hỏi bài tập?


