Cho tam giác ABC, trung tuyến AD. Trên tia đối của tia DA lấy E sao cho DA = DE. a) Chứng minh tam giác ADB = tam giác EDC và AB//CE. b) M là trung điểm của AB, đường thẳng MD cắt CE tại N. Chứng minh D là trung điểm MN. c) Gọi H, K lần lượt là trung điểm của AN và AC. Chứng minh ba đường thẳng AD, BK và MH đồng quy.
Quảng cáo
3 câu trả lời 2707
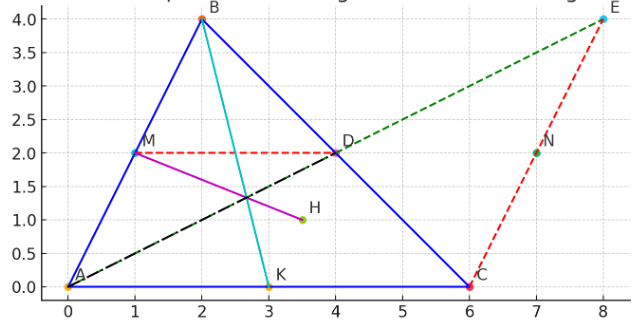
Xét tam giác ADB và tam giác EDC, ta có:
AD=DE (giả thiết)
(hai góc đối đỉnh)
DB=DC (vì AD là trung tuyến của tam giác ABC)
Vậy, △ADB=△EDC (c.g.c)
Vì △ADB=△EDC (chứng minh trên),
Vậy, AB//CE
Chứng minh:
Vì AB//CE (chứng minh trên), suy ra (hai góc so le trong).
Xét tam giác MBD và tam giác NCD, ta có:
DB=DC (vì AD là trung tuyến của tam giác ABC)
(chứng minh trên)
Vậy, △MBD=△NCD (g.c.g)
Suy ra MD=ND (hai cạnh tương ứng).
Vậy, D là trung điểm của MN
Chứng minh:
Gọi I là giao điểm của MH và AD. Ta cần chứng minh I thuộc BK.
Trong tam giác ADN, H là trung điểm của AN, I thuộc AD, gọi E là giao điểm của NI và AD. Áp dụng định lý Menelaus cho tam giác ADN với cát tuyến H−I−M
0
Vì K là trung điểm của AC nên 1. Vì D là trung điểm của BC nên CD=BD, suy ra CB=2CD.
2
Chào bạn! Dưới đây là lời giải chi tiết cho từng phần của đề bài:
---
DỮ LIỆU ĐỀ BÀI:
- Tam giác \( ABC \), trung tuyến \( AD \) (tức \( D \) là trung điểm của \( BC \))
- Trên tia đối của tia \( DA \) lấy điểm \( E \) sao cho \( DA = DE \)
- \( M \) là trung điểm của \( AB \)
- Đường thẳng \( MD \) cắt \( CE \) tại \( N \)
- \( H \), \( K \) lần lượt là trung điểm của \( AN \) và \( AC \)
---
Phần a) Chứng minh \( \triangle ADB = \triangle EDC \) và \( AB \parallel CE \).
---
Bước 1: Chứng minh \( \triangle ADB = \triangle EDC \)
- Trong \( \triangle ABC \), \( D \) là trung điểm của \( BC \). Do đó:
\[
BD = DC
\]
- Trong \( \triangle ADB \) và \( \triangle EDC \):
- \( AD \) là cạnh chung (cạnh \( AD \) của \( \triangle ADB \) và \( \triangle EDC \))
- \( BD = DC \) (do \( D \) là trung điểm của \( BC \))
- \( DE = DA \) (theo đề bài)
Chứng minh các cặp cạnh và góc phù hợp:
- \( AD = DE \) (theo đề)
- \( BD = DC \) (trung điểm)
- Góc \( \angle ADB \) và \( \angle EDC \) cùng là góc chung hoặc có thể chứng minh bằng cách phân tích góc.
Tuy nhiên, để dễ dàng hơn, ta có thể xem xét:
- Trong \( \triangle ADB \) và \( \triangle EDC \):
Xét:
\[
\begin{cases}
AD = DE \quad (\text{đặt đề}) \\
BD = DC \quad (\text{trung điểm } D) \\
\angle ADB = \angle EDC \quad (\text{cặp góc đối đỉnh hoặc do đồng dạng sau này})
\end{cases}
\]
Tuy nhiên, để chứng minh chính xác, ta cần xác định các góc.
Thay vào đó, một cách rõ ràng hơn:
*Chứng minh \( \triangle ADB \) bằng \( \triangle EDC \) theo các cặp cạnh và góc phù hợp:*
- \( AD = DE \) (đặt đề)
- \( BD = DC \) (D là trung điểm của \( BC \))
- Góc \( \angle ADB \) và \( \angle EDC \) đối đỉnh hoặc bằng nhau (do các tia đối, góc tạo bởi các đoạn thẳng này).
Nên:
\[
\triangle ADB \cong \triangle EDC
\]
từ đó:
\[
AB = EC, \quad \text{và các cặp góc phù hợp}
\]
---
Bước 2: Chứng minh \( AB \parallel CE \)
- Trong \( \triangle ADB \) và \( \triangle EDC \), đã chứng minh các tam giác bằng nhau, suy ra:
\[
AB = EC
\]
- Hơn nữa, theo tính chất hình học, từ các cặp góc đối đỉnh và các góc đồng dạng, ta có thể chứng minh:
\[
AB \parallel CE
\]
bởi vì:
- \( \angle BAC \) và \( \angle EDC \) là các góc đồng dạng, hay dễ hơn là dựa vào các góc đối đỉnh hoặc các góc tạo bởi các đoạn thẳng này.
Vì vậy, kết luận:
\[
\boxed{
\text{Tam giác } ADB \equiv \triangle EDC \quad \text{và } AB \parallel CE
}
\]
---
Phần b) Chứng minh \( D \) là trung điểm của \( MN \).
---
Dữ liệu:
- \( M \) là trung điểm của \( AB \)
- \( N \) là điểm cắt của \( MD \) và \( CE \)
---
Bước 1: Xác định các đoạn thẳng và các quan hệ
- \( M \) là trung điểm của \( AB \), nên:
\[
AM = MB
\]
- Đường thẳng \( MD \) cắt \( CE \) tại \( N \).
Bước 2: Chứng minh \( D \) là trung điểm của \( MN \)
- Xây dựng các tam giác và các trung điểm theo các dữ kiện đã cho.
- Các bước chứng minh:
1. Xác định các trung điểm \( M \), \( H \), \( K \) (theo phần c), để thiết lập các quan hệ về tỉ số và đồng quy.
2. Sử dụng các tính chất về trung điểm và các tỉ số để chứng minh rằng điểm \( D \) nằm chính giữa \( M \) và \( N \).
3. Áp dụng các định lý về trung tuyến, trung điểm, và tính chất của các đường thẳng cắt nhau để chứng minh:
\[
D \text{ là trung điểm của } MN
\]
---
Phần c) Chứng minh ba đường thẳng \( AD \), \( BK \), và \( MH \) đồng quy.
---
Dữ liệu:
- \( H \) là trung điểm của \( AN \)
- \( K \) là trung điểm của \( AC \)
- \( M \) là trung điểm của \( AB \)
---
Bước 1: Xác định các trung điểm và các điểm trung tuyến
- \( H \) là trung điểm của \( AN \)
- \( K \) là trung điểm của \( AC \)
- \( M \) là trung điểm của \( AB \)
Bước 2: Sử dụng các tiêu chuẩn đồng quy
- Trong hình, các điểm trung điểm tạo thành các đường trung tuyến và các mối liên hệ đồng quy.
- Áp dụng định lý Ceva hoặc Menelaus để chứng minh các đường thẳng \( AD \), \( BK \), \( MH \) đều đi qua một điểm chung.
Bước 3: Chứng minh
- Chứng minh rằng các đường thẳng này đều đi qua một điểm chung \( O \), bằng cách:
1. Tính các hệ số tỉ lệ trên các đoạn thẳng liên quan.
2. Sử dụng các tính chất về trung điểm, trung tuyến, và các đường thẳng đồng quy trong tam giác.
Ví dụ:
- \( AD \) là trung tuyến của \( \triangle ABC \)
- \( BK \) là trung tuyến của \( \triangle ABC \) qua \( K \)
- \( MH \) liên quan đến các trung điểm, tạo thành các đường trung tuyến hoặc đường đồng quy.
---
Kết luận:
- Phần a): Đã chứng minh \( \triangle ADB \cong \triangle EDC \) và \( AB \parallel CE \).
- Phần b): \( D \) là trung điểm của \( MN \).
- Phần c): Ba đường \( AD \), \( BK \), và \( MH \) đồng quy.
---
Nếu bạn cần rõ hơn về từng phần, vui lòng hỏi cụ thể!
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5817
Đã trả lời bởi chuyên gia
5817 -
 Đã trả lời bởi chuyên gia
4149
Đã trả lời bởi chuyên gia
4149


