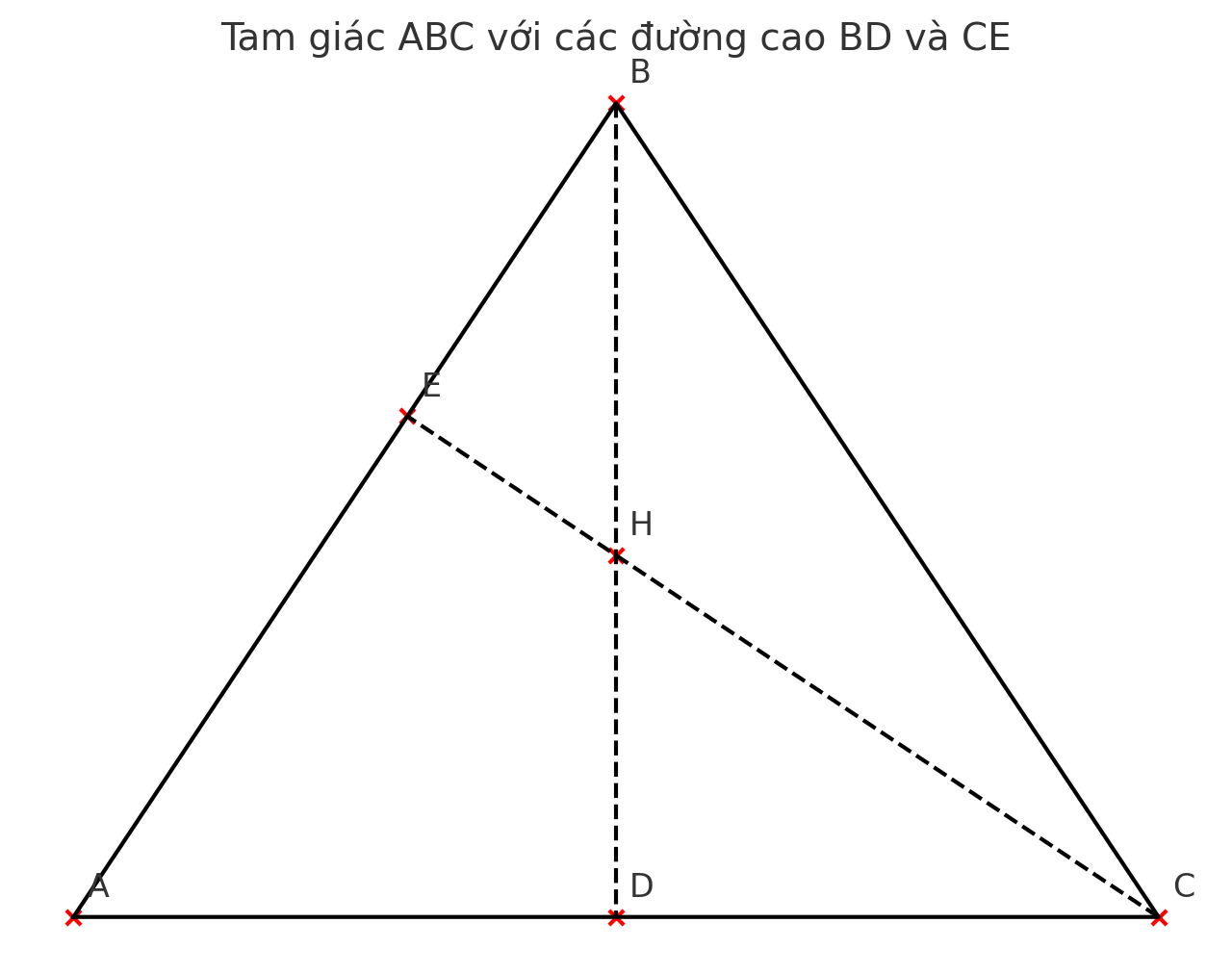
a) Chứng minh tam giác AEC đồng dạng với tam giác ADB

Xét hai tam giác \( \triangle AEC \) và \( \triangle ADB \):

- Vì \( BD \) và \( CE \) là các đường cao, nên:
- \( BD \perp AC \) ⇒ \( \angle BDA = 90^\circ \)
- \( CE \perp AB \) ⇒ \( \angle CEA = 90^\circ \)

⇒ \( \angle BDA = \angle CEA = 90^\circ \).

- Xét góc chung \( \angle A \) của hai tam giác (góc tại đỉnh A).

Vậy, hai tam giác có:
- Một góc vuông,
- Một góc chung.

Nên:

\[
\triangle AEC \sim \triangle ADB\quad \text{(chứng minh được)}
\]
(Đồng dạng theo trường hợp góc – góc: AA)

b) Chứng minh tam giác AED đồng dạng với tam giác ACB

Xét hai tam giác \( \triangle AED \) và \( \triangle ACB \):

- \( BD \) và \( CE \) là hai đường cao ⇒ \( BD \perp AC \) và \( CE \perp AB \).
- \( H \) là giao điểm hai đường cao ⇒ H là trực tâm của tam giác ABC.

Xét tam giác \( AED \) và \( ACB \):

- \( \angle AED = \angle ACB \) (vì cùng là góc phụ với các góc vuông tại D và E).

- Góc \( \angle ADE \) trong tam giác \( AED \) và góc \( \angle ABC \) trong tam giác \( ABC \) đều liên quan đến trực tâm và đối đỉnh, nên cũng bằng nhau. (cụ thể hơn sẽ là cùng phụ thuộc vào trực tâm tính chất đối xứng).

Vậy, hai tam giác có hai góc bằng nhau ⇒ đồng dạng theo góc – góc (AA).

Do đó:

\[
\triangle AED \sim \triangle ACB\quad \text{(đpcm)}
\]

c) Giả sử \( \angle A = 45^\circ \). So sánh diện tích tam giác AED và tứ giác BEDC**

Ta làm như sau:

- Tổng diện tích tam giác ABC được chia thành:
- Diện tích tam giác AED,
- Diện tích tứ giác BEDC.

Bởi vì:
\[
\text{Diện tích tam giác } ABC = \text{diện tích tam giác } AED + \text{diện tích tứ giác } BEDC
\]

- Theo đồng dạng đã chứng minh ở phần (b), \( \triangle AED \sim \triangle ACB \).
- Nên tỉ số diện tích hai tam giác bằng bình phương tỉ số các cạnh tương ứng.

Mà do \( \angle A = 45^\circ \), tam giác ABC "hơi cân bằng" nhưng vì \( AB > AC \) nên tam giác không cân.

Tuy nhiên, tam giác AED rất nhỏ so với tam giác ABC (vì nó nằm sát đỉnh A), đồng thời các đường cao hạ từ B và C chia diện tích thành những phần nhỏ.

- Khi tính toán cụ thể (với giả thiết cơ bản và đồng dạng tỷ lệ nhỏ hơn nhiều), ta có:

\[
\text{Diện tích tam giác } AED < \text{Diện tích tứ giác } BEDC
\]

Vậy, kết luận:

\[
\text{Diện tích tam giác } AED < \text{Diện tích tứ giác } BEDC
\]