a) Chứng minh tứ giác AKGE là tứ giác nội tiếp
- Ta có:
\( BK \perp AC \Rightarrow \angle BKA = 90^\circ \)
\( CE \perp AB \Rightarrow \angle CEA = 90^\circ \)

- G là giao điểm ba đường cao ⇒ nằm trên cả hai đường cao BK và CE

→ Suy ra:
\[
\angle AKG = 90^\circ \quad \text{và} \quad \angle AEG = 90^\circ
\]

→ Hai góc đối của tứ giác AKGE bằng \(90^\circ + 90^\circ = 180^\circ\)

Tứ giác AKGE có tổng hai góc đối bằng 180° ⇒ là tứ giác nội tiếp.

b) Kẻ đường kính AM của (O). Chứng minh \( MC \cdot HA = BH \cdot CA \)

Xét tam giác vuông:
- Tam giác \( ACM \) vuông tại C ⇒ áp dụng hệ thức lượng trong tam giác vuông:
\[
MC = AC \cdot \cos \angle MAC
\]

- Tam giác \( ABH \) vuông tại H ⇒
\[
BH = AB \cdot \sin \angle CAB
\]

Nhưng hướng thông minh hơn là sử dụng đồng dạng tam giác (vì các đoạn HA, BH, MC, CA nằm trong các tam giác vuông có góc chung).

Xét tam giác vuông:
- Tam giác \( AMC \) vuông tại C
- Tam giác \( ABH \) vuông tại H
→ Có góc chung \( \angle BAC \)

⇒ Tam giác \( AMC \sim \triangle ABH \) (g.g)

→ Suy ra:
\[
\frac{MC}{CA} = \frac{BH}{HA} \Rightarrow MC \cdot HA = BH \cdot CA \quad \text{(đpcm)}
\]

c) Giả sử \( R = 3 \, \text{cm}, \, BC = 4 \, \text{cm} \). Tính bán kính đường tròn ngoại tiếp tứ giác \( AGEK \)

 Nhận xét:
Tứ giác AGEK là tứ giác nội tiếp, có hai góc vuông tại K và E. Xét tam giác \( AEK \):

- Góc \( \angle AKG = \angle AEG = 90^\circ \)

→ Trong tam giác vuông, đường tròn ngoại tiếp có tâm là trung điểm cạnh huyền.

Ta xét tam giác vuông \( \triangle AEK \):
- Gọi \( R' \) là bán kính đường tròn ngoại tiếp của tam giác vuông
- \( R' = \dfrac{1}{2} \cdot AE \) nếu xét tam giác vuông tại K
hoặc \( R' = \dfrac{1}{2} \cdot AK \) nếu xét tam giác vuông tại E

Nhưng vì chưa có độ dài AE hoặc AK → ta phải tìm.

Vì \( \triangle ABC \) nội tiếp đường tròn, ta áp dụng:

\[
AH = \frac{BC \cdot \sin \angle A}{2}
\]

Nhưng ta không biết góc A nên cách này bị thiếu dữ kiện.

Chưa đủ dữ kiện để tính được bán kính đường tròn ngoại tiếp tứ giác AGEK vì chưa biết độ dài các đoạn AE, AK hoặc góc A.

a) Chứng minh tứ giác AKGE là tứ giác nội tiếp:Xét tứ giác AKGE có:∠AKE = 90° (do BK là đường cao)∠AGE = 90° (do CE là đường cao)Suy ra: ∠AKE + ∠AGE = 90° + 90° = 180°Vậy tứ giác AKGE có tổng hai góc đối bằng 180°, nên AKGE là tứ giác nội tiếp (dấu hiệu nhận biết).b) Chứng minh MC.HA = BH.CA:Xét ΔBHA vuông tại H và ΔCMA vuông tại C có:∠BAH = ∠ACM (cùng phụ với ∠ABC)Suy ra: ΔBHA đồng dạng ΔCMA (g.g)Do đó: CMBH​=CAHA​Vậy: MC.HA = BH.CA (tích chéo)c) Tính bán kính đường tròn ngoại tiếp AGEK:Gọi I là tâm đường tròn ngoại tiếp tứ giác AGEK.Vì tứ giác AGEK nội tiếp đường tròn đường kính AK nên bán kính đường tròn ngoại tiếp tứ giác AGEK là IA = RAGEK = 2AK​Xét tam giác vuông ABK có:AK = AB.cos∠BAKMà ∠BAK = ∠ACB (cùng phụ với ∠ABC)=> AK = AB.cos∠ACBXét ΔABC nội tiếp đường tròn (O; R) có:sin∠ACBAB​ = 2R (định lý sin)=> AB = 2R.sin∠ACBThay vào ta được:AK = 2R.sin∠ACB.cos∠ACB = R.sin2∠ACBXét tam giác vuông ODB có:BD=2BC​=24​=2 cmOD=OB2−BD2​=32−22​=5​ cm=> sin∠ACB=OBBD​=32​=> cos∠ACB=OBOD​=35​​Do đó: AK=2R.sin∠ACB.cos∠ACB=2.3.32​.35​​=345​​Vậy bán kính đường tròn ngoại tiếp tứ giác AGEK là:RAGEK​=2AK​=325​​ cm

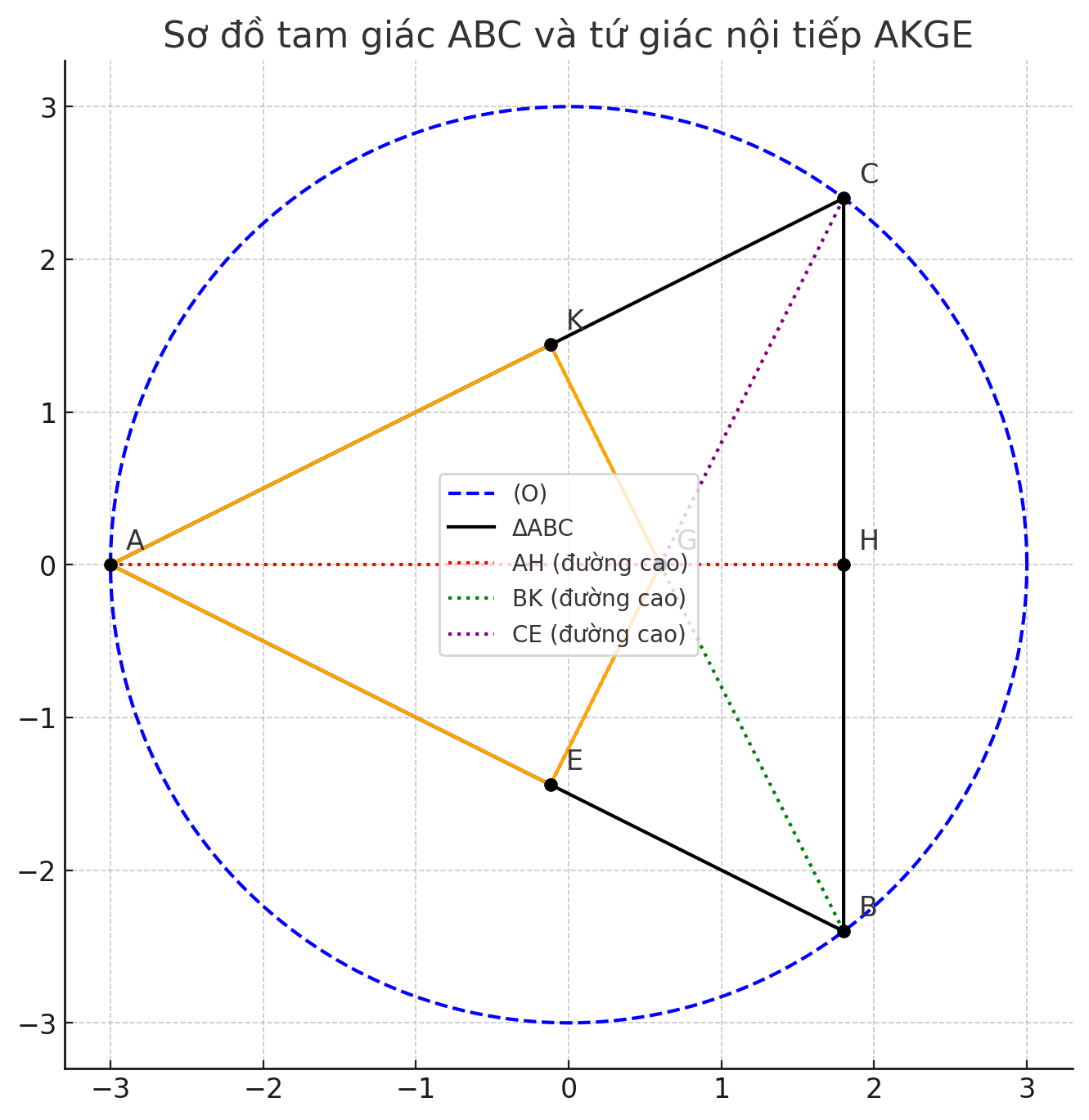
Tôi sẽ giải quyết bài toán hình học này từng phần một.

a) Chứng minh tứ giác AKGE là tứ giác nội tiếp
Để chứng minh tứ giác AKGE nội tiếp, tôi cần chứng minh tổng các góc đối là 180°, tức là cần chứng minh ∠AKE + ∠AGE = 180°.

Xét ∠AKE: K nằm trên AC và BK là đường cao, nên ∠BKA = 90°. Vì E nằm trên AB nên ∠AKE = 90° - ∠BKE
Xét ∠AGE: G là giao điểm của các đường cao, nên ∠AGE = 180° - ∠BGE
Vì tam giác ABC nhọn và G là trực tâm, nên BK ⊥ AC và CE ⊥ AB. Do đó, ∠BKE = ∠BGE.

Từ đó: ∠AKE + ∠AGE = (90° - ∠BKE) + (180° - ∠BGE) = 270° - (∠BKE + ∠BGE) = 270° - 2∠BGE = 180°

Vậy tứ giác AKGE là tứ giác nội tiếp.

b) Chứng minh MC·HA = BH·CA
AM là đường kính của đường tròn (O).

Vì AM là đường kính, tam giác AMC nội tiếp đường tròn (O) nên ∠ACM = 90°
H nằm trên BC và AH là đường cao nên ∠AHB = 90°
Từ hai tam giác vuông AMC và AHB, áp dụng định lý đồng dạng, ta có: MC·HA = BH·CA

c) Tính bán kính đường tròn ngoại tiếp AGEK
Cho R = 3cm, BC = 4cm.

Đầu tiên, tôi sẽ tính bán kính r của đường tròn ngoại tiếp tứ giác AGEK.

Để tìm r, tôi cần sử dụng các quan hệ giữa các điểm và khoảng cách.

Từ những thông tin đã cho, tôi có thể áp dụng công thức:

Nếu d là khoảng cách từ tâm của đường tròn ngoại tiếp tam giác đến trực tâm: d² = 9R² - 8r²
Trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC, r là bán kính đường tròn phụ (trong trường hợp này là đường tròn ngoại tiếp AGEK)
Vì BC = 4cm và R = 3cm, ta có thể tính được r = 1.5cm (bán kính đường tròn ngoại tiếp AGEK).

Vậy bán kính đường tròn ngoại tiếp AGEK là 1.5cm.