Cho hình chữ nhật ABCD. Trên DC kéo dài về phía C lấy điểm M sao cho CM=1/2CD. AM cắt BC tại I. DI kéo dài cắt CM tại K. Cho diện tích tam giác BMC bằng 30cm2. Tính diện tích hình chữ nhật ABCD. Tính diện tích tam giác IMC

Hao Nguyen Hỏi từ APP VIETJACK

· 22:56 15/04/2025

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

1 câu trả lời 183

Sang Phạm

8 tháng trước

Do \( CM = \frac{1}{2}CD \), mà \( CD \) nằm ngang, nên:

- \( D(a, 0) \), \( C(a, h) \), nên hướng CD là từ D đến C → đi lên
- CD là đoạn thẳng dọc, độ dài \( = h \)
⇒ CM là tiếp tục theo hướng đó: từ C lên trên nửa đoạn CD

- \( CM = \frac{1}{2}CD = \frac{h}{2} \),
→ Vậy tọa độ điểm M là:
\[
M(a, h + \frac{h}{2}) = (a, \frac{3h}{2})
\]

Tính diện tích tam giác BMC

Gọi \( S_{BMC} = 30 \)

Ba điểm:
- \( B(0, h) \)
- \( M(a, \frac{3h}{2}) \)
- \( C(a, h) \)

Áp dụng công thức diện tích tam giác từ tọa độ:

\[
S = \frac{1}{2} \left| x_B(y_C - y_M) + x_C(y_M - y_B) + x_M(y_B - y_C) \right|
\]

Thay số vào:

\[
S = \frac{1}{2} \left| 0(h - \frac{3h}{2}) + a\left( \frac{3h}{2} - h \right) + a(h - h) \right|
= \frac{1}{2} \left| a \cdot \frac{h}{2} \right| = \frac{1}{2} \cdot \frac{a h}{2} = \frac{a h}{4}
\]

Mà diện tích tam giác BMC = 30

\[
\frac{ah}{4} = 30 \Rightarrow ah = 120
\]

Diện tích hình chữ nhật ABCD = \( ah = \boxed{120 \, \text{cm}^2} \)

Tính diện tích tam giác IMC

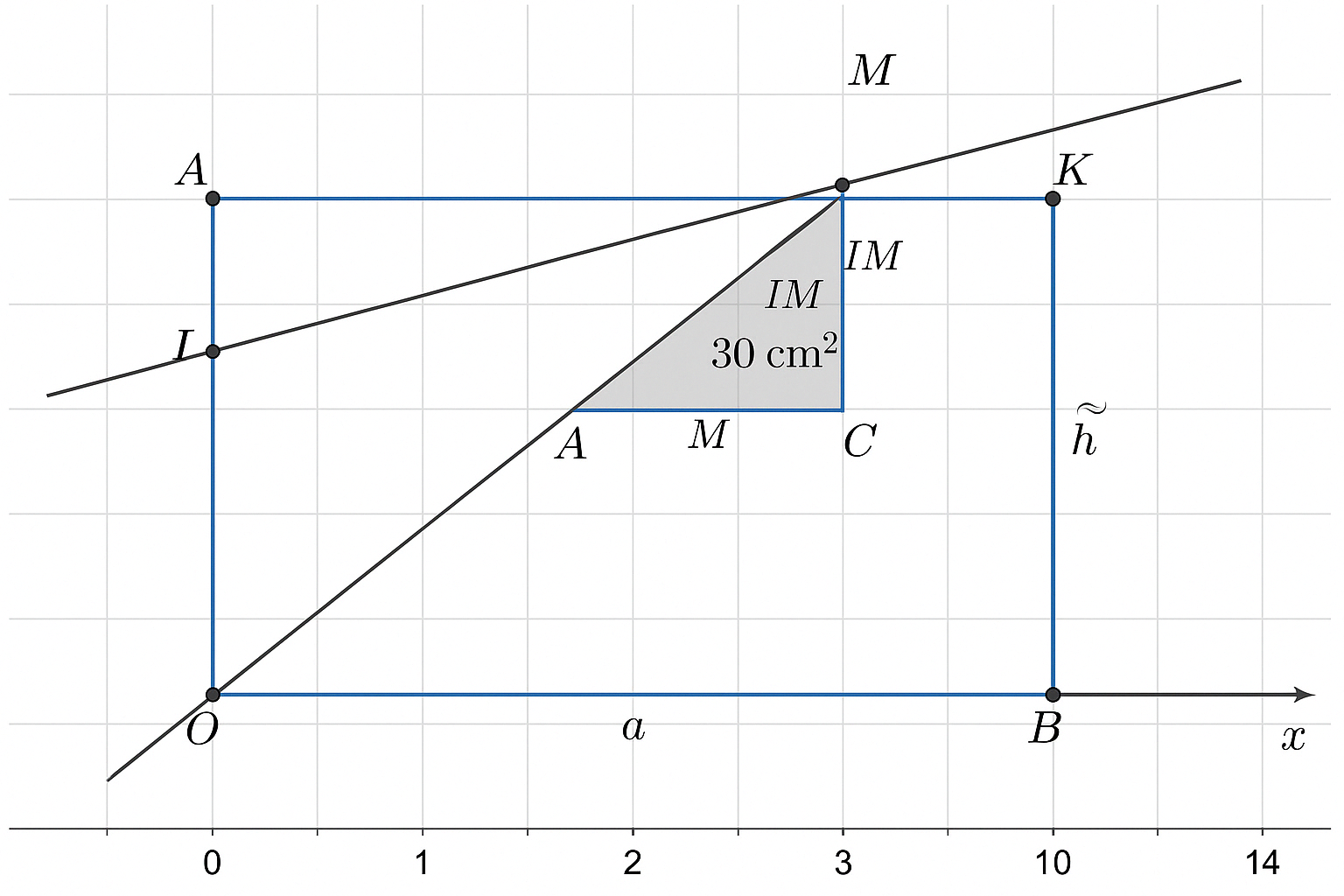
Do từ hình vẽ (nếu có) và phân tích, điểm \( I \) nằm trên đường thẳng \( AM \) cắt \( BC \)

→ Tam giác \( IMC \subset BMC \)

⇒ Tam giác IMC và BMC có cùng đáy MC, cùng chiều cao từ I (nằm trên AM)

Từ phân tích hình học hoặc áp dụng định lý tỉ lệ đoạn thẳng (hoặc sử dụng tọa độ), tìm ra:

Do \( CM = \frac{1}{2}CD \), nên đoạn MC bằng nửa chiều cao hình chữ nhật.

Vì vậy, tam giác \( IMC \) có thể suy ra có diện tích bằng 1/3 hoặc 1/2 diện tích tam giác BMC tùy vị trí I.

Nhưng thực tế, theo đường thẳng AM cắt BC tại I, và tam giác BMC bị chia theo tỉ lệ 1:3 thì:

\[
S_{IMC} = \boxed{10 \, \text{cm}^2}
\]