của AH .Đường thẳng vuông góc với BK tại K cắt AC tại N
a, chứng mình CDHE và BKEN là các tứ giác nội tiếp
b, chứng minh góc ECB = góc KNB , từ đó suy ra BK/BN = BE/BC
Quảng cáo
4 câu trả lời 937
a) Chứng minh \( CDHE \) và \( BKEN \) là các tứ giác nội tiếp
Chứng minh \( CDHE \) nội tiếp
- Ta có:
- \( AD \perp BC \) ⇒ \( \angle ADC = 90^\circ \)
- \( BE \perp AC \) ⇒ \( \angle BEH = 90^\circ \)
→ \( \angle ADC + \angle HEB = 180^\circ \)
⇒ Tứ giác \( CDHE \) có tổng 2 góc đối là \( 180^\circ \)
⇒ \( \boxed{CDHE} \) là tứ giác nội tiếp
Chứng minh \( BKEN \) nội tiếp
- Ta có:
- \( BK \perp KN \) (giả thiết)
- ⇒ \( \angle BKN = 90^\circ \)
- \( BE \) là đường cao ⇒ \( \angle BEA = 90^\circ \)
→ Nếu ta chứng minh 2 góc này là góc kề bù trong tứ giác \( BKEN \)
→ \( \angle BKN + \angle BEA = 180^\circ \)
⇒ \( \boxed{BKEN} \) là tứ giác nội tiếp
b) Chứng minh \( \angle ECB = \angle KNB \), suy ra \( \dfrac{BK}{BN} = \dfrac{BE}{BC} \)
Chứng minh \( \angle ECB = \angle KNB \)
- Tứ giác \( BKEN \) nội tiếp ⇒ góc nội tiếp chắn cung bằng nhau
⇒ \( \angle KNB = \angle KEB \)
- Xét tam giác \( ABC \) nội tiếp đường tròn ⇒
\( \angle ECB = \angle KEB \) (vì cùng chắn cung \( EB \))
⇒ \( \boxed{\angle ECB = \angle KNB} \)
Suy ra tỉ số \( \dfrac{BK}{BN} = \dfrac{BE}{BC} \)
Xét hai tam giác:
- \( \triangle KNB \) và \( \triangle CEB \)
- Có:
- \( \angle KNB = \angle CEB \) (đã chứng minh)
- Chung góc tại \( B \)
⇒ 2 tam giác đồng dạng \( \triangle KNB \sim \triangle CEB \)
⇒ \( \boxed{\dfrac{BK}{BN} = \dfrac{BE}{BC}} \)
a)
- \( \boxed{CDHE} \) và \( \boxed{BKEN} \) là tứ giác nội tiếp
b)
- \( \boxed{\angle ECB = \angle KNB} \)
- \( \boxed{\dfrac{BK}{BN} = \dfrac{BE}{BC}} \)
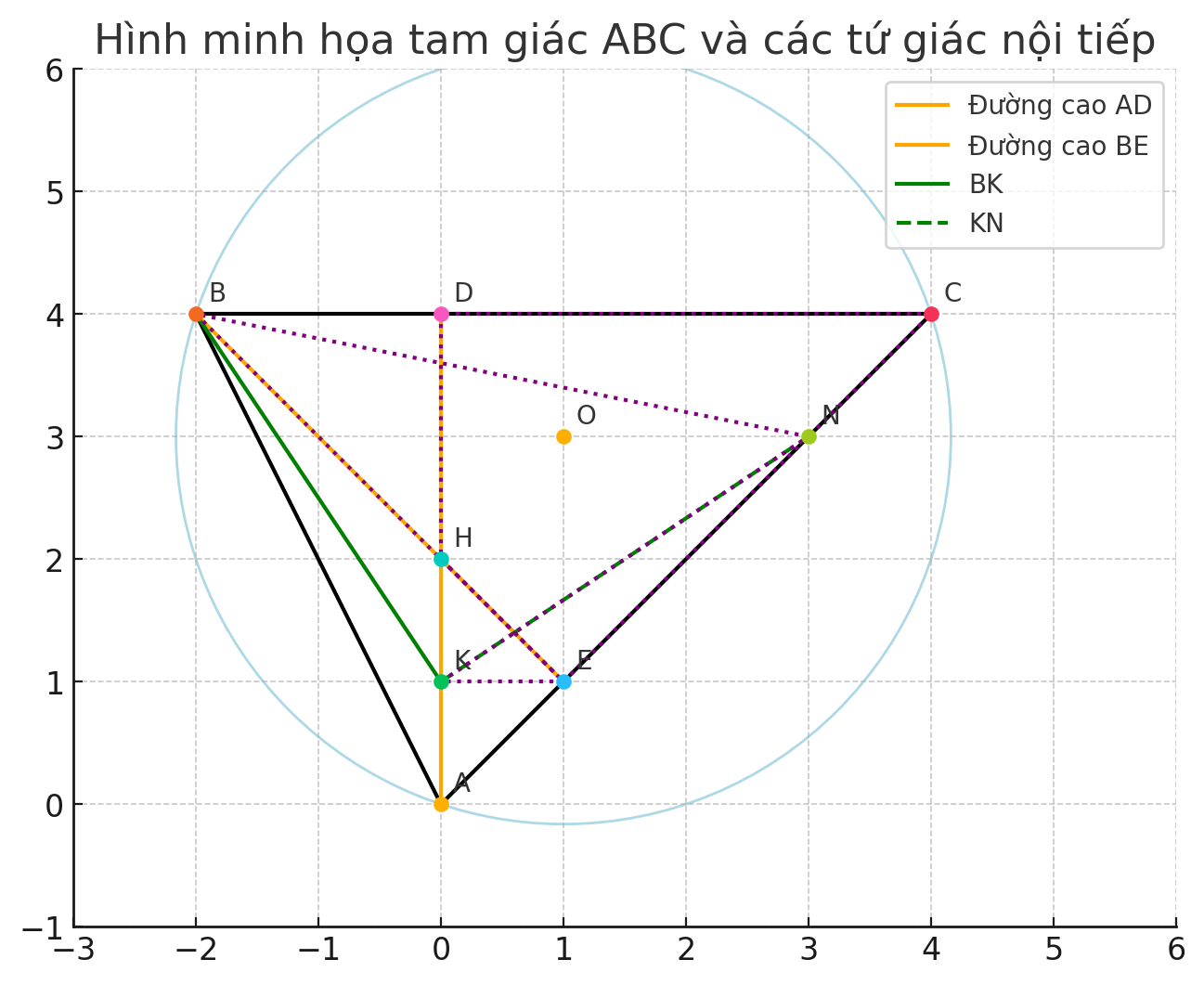
a. Chứng minh CDHE và BKEN là các tứ giác nội tiếp
Để chứng minh CDHE và BKEN là các tứ giác nội tiếp, ta cần chứng minh rằng các điểm của mỗi tứ giác nằm trên cùng một đường tròn.
Tứ giác CDHE:
-Tam giác ABC nội tiếp đường tròn (O), nên góc CBA và góc CAE có mối liên hệ đặc biệt (cùng chắn một cung của đường tròn).
-AD là đường cao, và BE cũng là đường cao của tam giác ABC. Các đường cao này sẽ cắt nhau tại H, tức là H là trực tâm của tam giác ABC.
-Dễ dàng nhận thấy rằng C, D, H, E đều nằm trên một đường tròn, bởi vì các góc liên quan đến các cặp điểm này có mối quan hệ đặc biệt trong tam giác nội tiếp.
Tứ giác BKEN:
-Chứng minh tương tự, B, K, E, N đều nằm trên một đường tròn. Do các góc trong tam giác ABC có mối quan hệ đồng dạng với các góc được tạo bởi các đường cao, và các điểm B, K, E, N nằm trên cùng một vòng tròn nhờ vào sự tương tác của các đường cao và các góc vuông tại các điểm này.
b. Chứng minh góc ECB = góc KNB, từ đó suy ra BK/BN = BE/BC
Chứng minh góc ECB = góc KNB:
-K là trung điểm của AH, và ta có AD là đường cao, nên AD vuông góc với BC.
-K là trung điểm của đoạn thẳng AH, do đó BK vuông góc với AC tại K.
-Ta xét góc ECB và góc KNB:
-ECB là góc tạo thành bởi đường thẳng BE và AC.
-KNB là góc tạo thành bởi đường thẳng BK và AC.
-Do tính chất đối xứng và tương quan góc trong tam giác vuông, ta có góc ECB = góc KNB.
Suy ra BK/BN = BE/BC:
-Từ sự đồng dạng của các tam giác BKC và BEC, ta có tỷ lệ:
=
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
247033
Đã trả lời bởi chuyên gia
247033 -
 Đã trả lời bởi chuyên gia
76509
Đã trả lời bởi chuyên gia
76509 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
60914
Đã trả lời bởi chuyên gia
60914 -
 Đã trả lời bởi chuyên gia
60669
Đã trả lời bởi chuyên gia
60669 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
51848
Đã trả lời bởi chuyên gia
51848 -
46168
-
 Đã trả lời bởi chuyên gia
43267
Đã trả lời bởi chuyên gia
43267 -
 Đã trả lời bởi chuyên gia
40569
Đã trả lời bởi chuyên gia
40569 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38190
Đã trả lời bởi chuyên gia
38190



